- •Вопрос № 1 Понятие матрицы. Виды матриц
- •Вопрос № 2 Сложение матриц. Умножение матрицы на число
- •Вопрос № 3 Произведение матриц
- •Вопрос № 5 Определители матриц. Свойства определителей
- •Вопрос № 18
- •Вопрос № 12-(33) Замечательные пределы.
- •Вопрос № 14-(34) Односторонние и двусторонние пределы функции. Точки разрыва и их классификации
- •Вопрос № 9
- •Сравнение бесконечно малых величин. Бесконечно большая величина. Правило Лопиталя. Раскрытие неопределенностей типа 0/0, бесконечность/ бесконечность
- •Вопрос № 7
- •Вопрос № 10 Решение систем линейных уравнений методом Гаусса
- •Вопрос № 8 Матрица, обратной данной и ее вычисление
- •Вопрос № 20-(40) Производные высших порядков Механистический смысл 2ой производной
- •Вопрос № 19-(39) Производные сложной и обратной функции
- •Доказательство
- •Доказательство
- •Вопрос № 22-(42) Теорема Роля, Коши, Лангранжа о дифференцируемых функциях
- •Билет № 17-(37) Правило дифференцирования. Таблица производных
- •Вопрос № 16-(36)
- •Вопрос № 15-(35)
- •Геометрический смысл производной
- •Механический смысл производной
- •Вопрос № 10-(43)
- •Вопрос № 8-(44) Экстремум функции и критические точки. Необходимое экстемума фукции
- •Вопрос № 7-(43)
- •Вопрос № 6-(46) Асимптомы графика функции. Общая схема исследования функции и построение графиков
- •Вопрос № 20 Параллельный перенос и поворот осей координат
- •Вопрос № 21 Общее уравнение прямой. Уравнение прямой с угловым коэффициентом
- •Вопрос № 23 Нормальное уравнение прямой. Расстояние от точки до прямой
- •Вопрос № 1-(24) Угол между прямыми. Условие параллельности и перпендикулярности прямых
- •Вопрос № 11 Методом Крамера
- •Вопрос № 13 Понятие вектора. Операции над векторами в геометрической форме
- •Вопрос № 14 Проекции вектора на ось и ее свойства
- •Вопрос № 15 Разложение вектора по ортам координатных осей
- •Вопрос № 14-(32) Теоремы о непрерывных функциях.
- •Вопрос № 11-(30) Бесконечно малые величины (функции). Теоремы о бесконечно малых величинах
- •Вопрос № 10-(29) Понятие последовательности и ее предела. Предел функции. Теоремы о пределах
- •Уравнение параболы и исследование ее формы
- •Вопрос № 5-(27) Уравнение гиперболы и исследование ее формы. Эксцентриситет и ассимптоматы гиперболы
- •Вопрос № 4-(25)
Вопрос № 20 Параллельный перенос и поворот осей координат
Параллельный перенос осей координат
Пусть на плоскости задана прямоугольная система координат Оху. Под параллельным переносом осей координат понимают переход от системы координат Оху к новой системе O1x1y 1, при котором меняется положение начала координат, а направление осей и масштаб остаются неизменными.
|
|
|
|
|
|
Пусть
начало новой системы координат точка
О1
имеет координаты (x0;y0)
в старой системе координат Оxy,
т.е. О1(x0;y0).
Обозначим координаты произвольной
точки М плоскости в системе Oxy
через (x;y),
а в новой системе О1x1y1
через
![]() (см.
рис. 6).
(см.
рис. 6).
Рассмотрим векторы
![]()
![]()
![]()
Так
как
![]() то
то
![]() т.е.
т.е.
![]()
Следовательно
Полученные формулы позволяют находить старые координаты х и у по известным новым х' и у' и наоборот.
Поворот осей координат
П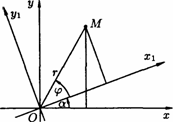 од
поворотом
осей координат
понимают такое преобразование координат,
при котором обе оси поворачиваются на
один и тот же угол, а начало координат
и масштаб остаются неизменными.
од
поворотом
осей координат
понимают такое преобразование координат,
при котором обе оси поворачиваются на
один и тот же угол, а начало координат
и масштаб остаются неизменными.
Пусть новая система 0\х\у\ получена поворотом •системы Оху на угол а.
Пусть М — произвольная точка плоскости, (а;; у) — ее координаты в старой системе и (х', у') — в
новой системе.
Введём две полярные системы координат с общим полюсом О и полярными осями Ох и Oxi (масштаб одинаков). Полярный радиус г в обеих системах одинаков, а полярные углы соответственно равны a + j и j, где j - полярный угол в новой полярной системе.
По формулам перехода от полярных координат к прямоугольным имеем
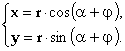 т.е.
т.е.
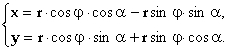
Но
![]() и
и
![]()
П![]() оэтому
оэтому
Полученные формулы называются формулами поворота осей. Они позволяют определять старые координаты (x;у) произвольной точки М через новые координаты (х';у') этой же точки М, и наоборот.
Е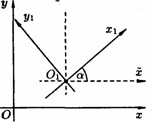 сли
новая система координат O1х1у1
получена из старой Оху
путем параллельного переноса осей
координат и последующим поворотом осей
на угол a
(см. рис. 30), то путем введения вспомогательной
системы
сли
новая система координат O1х1у1
получена из старой Оху
путем параллельного переноса осей
координат и последующим поворотом осей
на угол a
(см. рис. 30), то путем введения вспомогательной
системы
![]() легко
получить формулы
легко
получить формулы
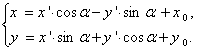
выражающие старые координаты х и у произвольной точки через её новые координаты х' и у'.
|
|
Вопрос № 21 Общее уравнение прямой. Уравнение прямой с угловым коэффициентом
Уравнение
Ах+Ву+С=0
(где А, В, С могут иметь любые значения, лишь бы коэффициенты А, В не были нулями оба сразу) представляет прямую линию. Всякую прямую можно представить уравнением этого вида. Поэтому его называют общим уравнением прямой.
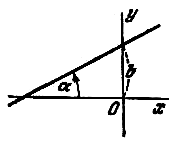
Угол
![]() ,
определяемый, как показано на рис.,
называется углом наклона прямой к оси
Ох. Тангенс угла наклона прямой к оси
Ох называется угловым коэффициентом
прямой; его обычно обозначают буквой
k:
,
определяемый, как показано на рис.,
называется углом наклона прямой к оси
Ох. Тангенс угла наклона прямой к оси
Ох называется угловым коэффициентом
прямой; его обычно обозначают буквой
k:
![]()
Уравнение
![]() называется
уравнением прямой с угловым коэффициентом;
k - угловой коэффициент, b - величина
отрезка, который отсекает прямая на оси
Оу, считая от начала координат.
называется
уравнением прямой с угловым коэффициентом;
k - угловой коэффициент, b - величина
отрезка, который отсекает прямая на оси
Оу, считая от начала координат.
Вопрос № 23 Нормальное уравнение прямой. Расстояние от точки до прямой
Если
обе части уравнения Ах + Ву + С = 0 разделить
на число
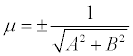 ,
которое называется нормирующем
множителем ,
то получим
,
которое называется нормирующем
множителем ,
то получим
xcosφ + ysinφ - p = 0 –
нормальное уравнение прямой.
Знак ± нормирующего множителя надо выбирать так, чтобы μ ? С < 0.
р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.