Вопрос № 8-(44) Экстремум функции и критические точки. Необходимое экстемума фукции

Функция y=f(x) называется возрастающей (убывающей) в некотором интервале, если при x₁< x₂ выполняется неравенство f(x₁) < f (x₂) (f(x₁) > f(x₂)).

Если дифференцируемая функция y = f(x) на отрезке [a, b] возрастает (убывает), то ее производная на этом отрезке f ¢(x) > 0 (f ¢(x) < 0).

Точка x_о называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки x_о, для всех точек которой верно неравенство f(x) £ f(x_о) (f(x) ³ f(x_о)).

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.

Необходимые условия экстремума. Если точка x_о является точкой экстремума функции f(x), то либо f ¢(x_о) = 0, либо f ¢(x_о) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x_о - критическая точка. Если f ¢ (x) при переходе через точку x_о меняет знак плюс на минус, то в точке x_о функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x_о экстремума нет.

Второе достаточное условие. Пусть функция f(x) имеет производную f ¢ (x) в окрестности точки x_о и вторую производную  в самой точке x_о. Если f ¢(x_о) = 0, >0 (<0), то точка x_о является точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].

Вопрос № 7-(43)

Выпуклость и вогнутость графика функции. Точка перегиба

        свойство графика функции у = f (x) (кривой), заключающееся в том, что каждая дуга кривой лежит не выше (не ниже) своей хорды; в первом случае график функции f (x) обращён выпуклостью книзу (вогнутостью кверху) и сама функция называется выпуклой (рис. 1, а), во втором — график обращён вогнутостью книзу (выпуклостью кверху) и функция называется вогнутой (рис. 1, б). Если существуют производные f '(x) и f "(х), то первый случай имеет место при условии, что f "(x) ≥ 0, а второй при f "(x) ≤ 0 (во всех точках рассматриваемого промежутка). Выпуклость (книзу) можно охарактеризовать также тем, что дуга кривой лежит не ниже касательной, в окрестности любой своей точки (рис. 2, a), а вогнутость (книзу) — тем, что дуга кривой лежит не выше касательной (рис. 2, б). Аналогично определяются В. и в. поверхности.

        

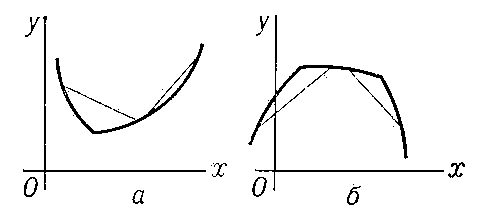
        Рис. 1 к ст. Выпуклость и вогнутость.

        

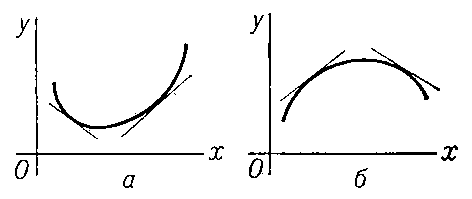
        Рис. 2 к ст. Выпуклость и вогнутость.

. Точка, в которой направление выпуклости графика функции меняется на противоположное называется точкой перегиба.

Вопрос № 6-(46) Асимптомы графика функции. Общая схема исследования функции и построение графиков

Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.

        Определение 7.1   Вертикальной асимптотой графика функции называется вертикальная прямая , если или при каком-либо из условий: , , . Заметим, что мы при этом не требуем, чтобы точка принадлежала области определения функции , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки: или , где .     

Наклонной асимптотой графика функции при называется прямая , если выполнены два условия: 1) некоторый луч целиком содержится в ; 2) расстояние по вертикали между графиком и прямой стремится к 0 при :

(7.1)

Наклонной асимптотой графика функции при называется прямая , если 1) некоторый луч целиком содержится в ; 2) расстояние по вертикали между графиком и прямой стремится к 0 при :

    

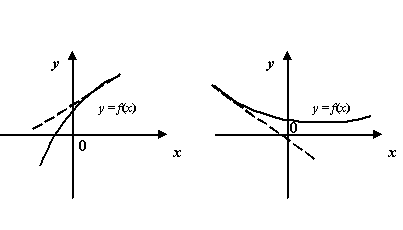
Рис.7.6.Графики функций, имеющие наклонные асимптоты при и при

В случае, если наклонная асимптота расположена горизонтально, то есть при , она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота -- частный случай наклонной асимптоты; прямая является горизонтальной асимптотой графика при или , если

или

соответственно.