Вопрос № 15-(35)

Производная функции — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называется дифференцированием.

Геометрический смысл производной

Пусть функция определена в некоторой окрестности токи , непрерывна в этой точке и , а (рис.2).

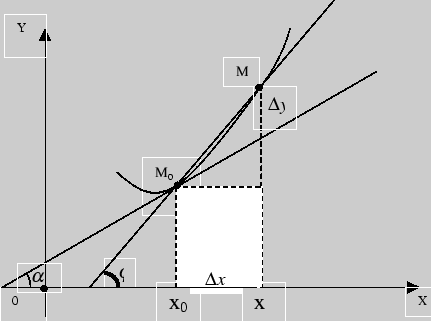
Рис. 2

Придав произвольное приращение аргументу , так чтобы , перейдем к точке с абсциссой и ординатой , где .

Уравнение прямой, проходящей через точки и (секущей графика функции , имеет вид: , где отношение представляет собой угловой коэффициент секущей (.

Касательной к графику функции в точке называется предельное положение секущей , при стремлении точки по графику к точке .

Для того, чтобы секущая при стремилась к предельному положению, отличному от вертикальной прямой , необходимо и достаточно, чтобы существовал конечный предел , то есть , чтобы существовала конечная производная функции в точке .

Угловой коэффициент касательной получается путем перехода от к пределу при :

Таким образом, получим, что , где - угол наклона касательной к оси (см. рис.), а значение производной равно угловому коэффициенту касательной к графику функции. В этом заключается геометрический смысл производной. Уравнение касательной к графику функции в точке имеет вид

В случае бесконечной производной .

Из уравнения секущей имеем:

Переходя в равенстве к пределу при , получаем уравнение касательной к графику функции в точке в виде , то есть касательная является в данном случае вертикальной прямой, проходящей через точку оси абсцисс.

Механический смысл производной

Пусть материальная точка движется прямолинейно и - длина пути, проходимого за время , отсчитываемого от некоторого момента времени .

Для определения скорости в данный момент придадим переменной некоторое приращение , при этом приращение пути будет равно .

Отношение называется в физике величиной средней скорости движения за промежуток времени, начиная с момента времени , и обозначается

Предел называется величиной мгновенной скорости движения в момент времени .

Таким образом, мгновенная скорость в момент времени прямолинейного движения, совершаемого по закону равна значению производной .

Вопрос № 10-(43)

НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ ВОЗРАСТАНИЯ И УБЫВАНИЯ ФУНКЦИИ

Вспомним сначала определения возрастающей и убывающей функций.

Функция y=f(x), определенная на некотором отрезке [a, b] (интервале (a, b)), называется возрастающей на этом отрезке, если большему значению аргумента x из [a, b] соответствует большее значение функции, то есть если x₁ < x₂, то f(x₁) < f(x₂).

Функцияy=f(x) называется убывающей на некотором отрезке [a, b], если меньшему значению аргумента x из [a, b]соответствует большее значение функции, то есть если x₁ < x₂, то f(x₁) > f(x₂).

Функция, только возрастающая или только убывающая на отрезке, называется монотонной на этом отрезке.

Функция y=f(x) называется постоянной на некотором отрезке [a, b], если при изменении аргумента x она принимает одни и те же значения.

Р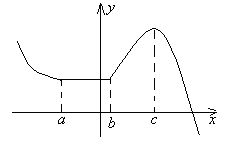ассмотрим график функции изображенной на рисунке и определим промежутки возрастания и убывания функции.

(-∞, a), (c, +∞) – убывает;

(a, b) – постоянная;

(b, c) – возрастает.

Применим понятие производной для исследования возрастания и убывания функции.

Теорема 1. (Необходимое и достаточное условия возрастания функции)

1. Если дифференцируемая функция y=f(x) возрастает на [a, b], то ее производная неотрицательна на этом отрезке, f '(x)≥ 0.

2. Обратно. Если функция y=f(x) непрерывна на [a, b], дифференцируема на (a, b) и ее производная положительна на этом отрезке,f ' (x)≥ 0 для a<x<b, то f(x) возрастает на[a, b].

Доказательство.

1. Докажем первую часть теоремы. Итак, пусть функция y=f(x) возрастает на [a, b]. Зафиксируем на этом отрезке произвольную точку x, придадим ей приращение Δx. Тогда если Δx>0, то x<x+Δx. Поэтому по определению возрастающей функции f(x)<f(x+Δx), то есть f(x+Δx) - f(x)>0. Но тогда и 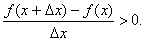Аналогично, если Δx<0, то x>x+Δx и значит f(x+Δx)-f(x)<0, а

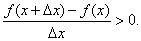
Переходя в этом равенстве к пределу при Δx→0, получим , то есть f '(x)≥0.

2. Докажем вторую часть теоремы. Пусть f '(x)>0при всех x Î (a,b). Рассмотрим два любых значения x₁ и x₂ таких, что x₁ < x₂. Нужно доказать, что f(x₁)< f(x₂). По теореме Лагранжа существует такое число c Î (x₁, x₂), что 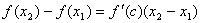. По условию f '(x)>0, x₁ – x₂>0Þ 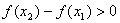, а это и значит, что f(x) – возрастающая функция.

Аналогичная теорема имеет место и для убывающих функций.

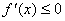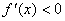Теорема 2. Если f(x) убывает на[a,b], то на этом отрезке. Если на (a; b), то f(x) убывает на [a, b],в предположении, чтоf(x) непрерывна на [a, b]. Доказанная теорема выражает очевидный геометрический факт. Если на [a, b] функция возрастает, то касательная к кривой y=f(x) в каждой точке этого отрезке образует острый угол с осью Ox или горизонтальна, т.е. tga≥0, а значит f '(x)≥0. Аналогично иллюстрируется и вторая часть теоремы. Таким образом, возрастание и убывание функции характеризуется знаком ее производной. Чтобы найти на каком промежутке функция возрастает или убывает, нужно определить, где производная этой функции только положительна или только отрицательна, то есть решить неравенства f '(x)>0 – для возрастания или f '(x)<0 – для убывания.