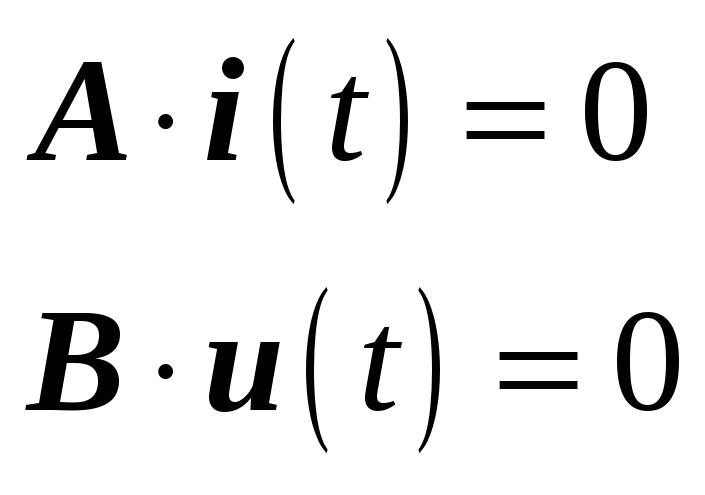- •Экзаменационная программа по курсу "Общая электротехника и электроника" (3 семестр, поток а-1, 2, 15-05)
- •Линейные электрические цепи со сосредоточенными параметрами. (постоянные)
- •Основные интегральные переменные.
- •Математические модели двухполюсных элементов электрической цепи (во временной области).
- •Основные подграфы.
- •Топологические матрицы.
- •Полная система уравнений цепи.
- •Уравнения Кирхгофа с записью источников в явном виде.
- •I. Принцип суперпозиции (метод наложения).
- •Определение коэффициентов метода наложения.
- •Способ расчёта цепи с помощью метода наложения.
- •II. Принцип компенсации.
- •Комплексная форма ряда Фурье.
- •Расширенный метод узловых потенциалов (расширенные узловые уравнения).
- •Передача мощности от активного двухполюсника к пассивному двухполюснику.
- •1). Последовательное соединение.
- •2). Параллельное соединение.
- •Операционный усилитель (оу).
- •Малосигнальная низкочастотная модель оу в линейном режиме.
- •Инвертирующий усилитель на базе оу.
- •Повторитель.
- •Частотные электрические фильтры.
- •Добротность контура.
- •Классический метод расчета переходных процессов в цепях 1-го порядка.
- •Классический метод расчета. Цепи 1-го порядка.
- •1. Схема в установившемся режиме до коммутации,
- •2. Схема после коммутации,
- •1). Линейность.
- •2). Преобразование Лапласа от производной.
- •3). Преобразование Лапласа от интеграла.
- •Решение уравнений состояния в операторной форме.
- •Схемное моделирование источников в виде функции .
- •Связь переходной и импульсной характеристик цепи с передаточной функцией цепи.
- •3. Метод дискретных линейных моделей.
Частотные электрические фильтры.
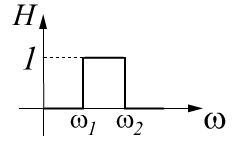
Четырехполюсники, предназначенные для передачи электрических сигналов одних частот и задерживания (подавления) электрических сигналов других частот называются фильтрами. Полоса пропускания электрического фильтра- диапазон частот, в котором электрический фильтр пропускает сигнал без искажения и ослабления (идеальный фильтр) или с малыми искажениями и ослаблениями (реальный фильтр).
Различают следующие типы искажений:
а). амплитудные искажения- нарушения соотношений между амплитудами различных гармоник.
б). фазовые искажения- нарушения соотношений между различными фазами гармоник.
в). искажения, связанные с ограничениями спектра передаваемого сигнала.

В зависимости от частотного диапазона, в котором пропускаются сигналы, существуют следующие типы фильтров (идеальных фильтров):
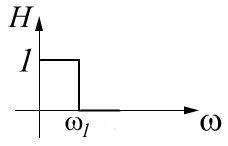
1). Фильтр низкой частоты (ФНЧ).
![]()
![]()
![]()
![]()
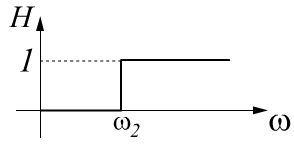
2). Фильтр высокой частоты (ФВЧ).
![]()
![]()
![]()
![]()
3). Полосно-пропускающий фильтр (ППФ).
![]()
![]()
![]()
![]()
![]()
4). Полосно-заграждающий фильтр (ПЗФ).

![]()

![]()
![]()
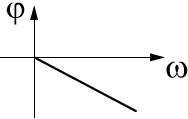
Требования к идеальному фильтру.
Для передачи сигнала без искажения АЧХ фильтра должна быть постоянной в полосе пропускания и ФЧХ должна изменяться по линейному закону.

![]()
![]()
БИЛЕТ 18. Фильтры 1-го порядка.
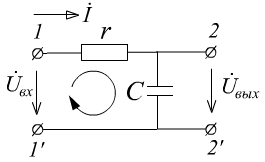
Фильтры 1-го порядка.
1.
![]()
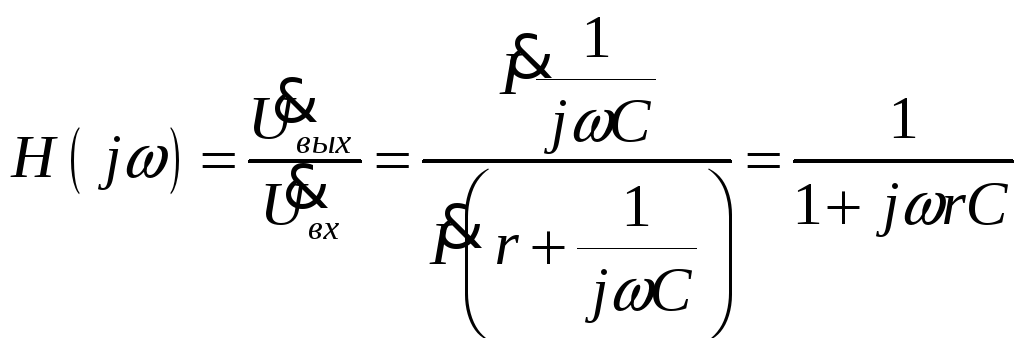
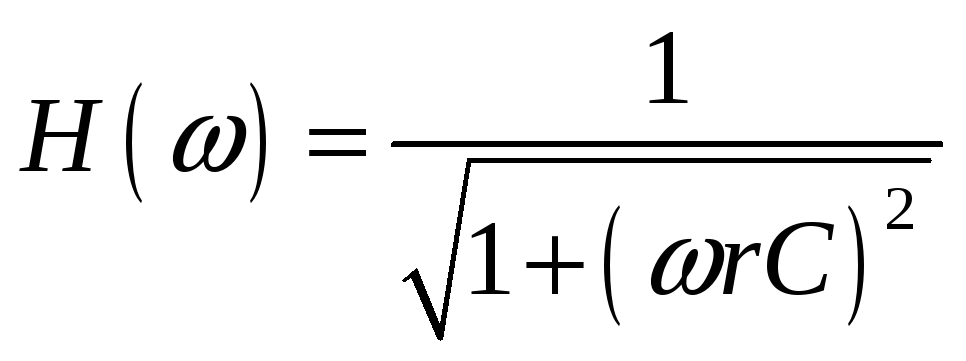
![]()

- ФНЧ
Порядок
фильтра определяется количеством
реактивных элементов в цепи, которое
определяет максимальную степень
![]() в знаменателе
в знаменателе![]() .
.
 -
каноническая форма записи передаточной
функции ФНЧ 1-го порядка.
-
каноническая форма записи передаточной
функции ФНЧ 1-го порядка.
![]()
2.

![]()
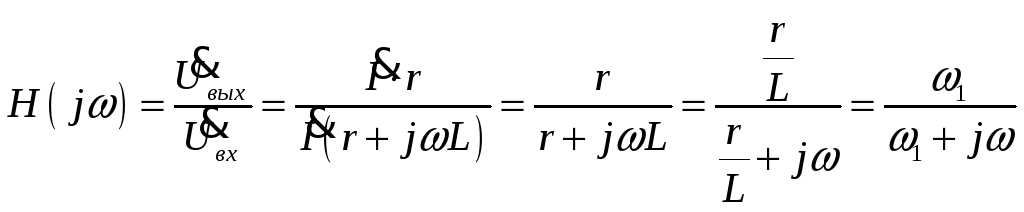 (
(![]() -
граничная частота)
-
граничная частота)
3.

![]()
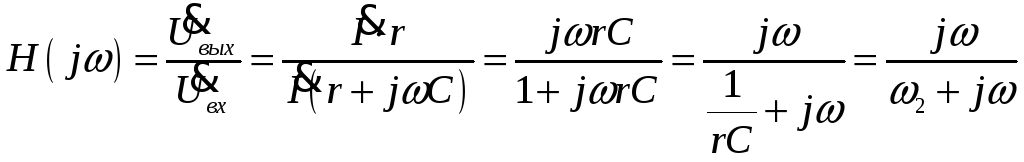 -
ФВЧ
-
ФВЧ
![]() ,
,
![]()
![]()
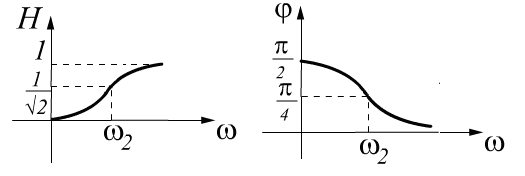
![]() -
разность фаз числителя и знаменателя.
-
разность фаз числителя и знаменателя.
4.
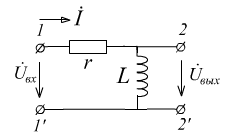
![]()
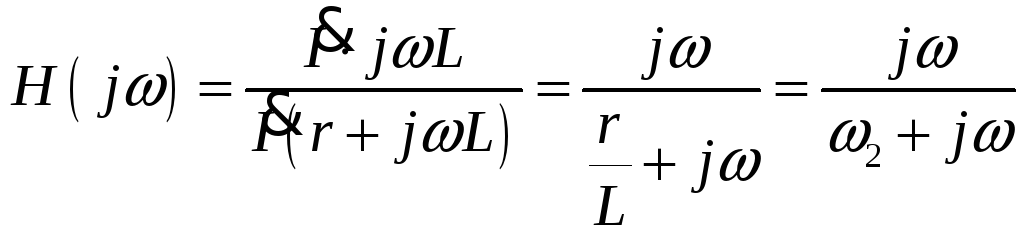 -
ФВЧ
-
ФВЧ
![]()
БИЛЕТ 19. Частотные характеристики последовательной RLC-цепи. Входное сопротивление, добротности RLC-цепи.

![]()
![]()
![]()
![]() -
резонансная частота.
-
резонансная частота.

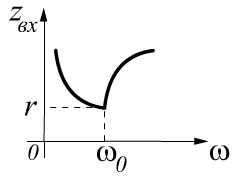
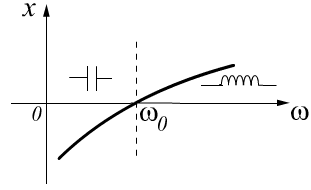

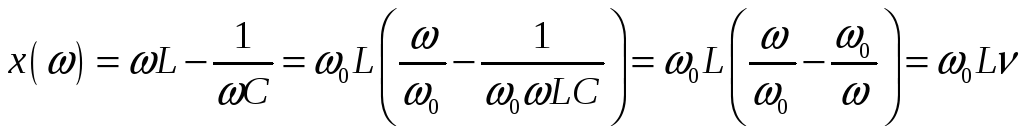
![]() -
расстройка частот.
-
расстройка частот.
Рассмотрим
резонанс напряжений при
![]() :
:
![]()
![]()

![]()
![]()
Добротность контура.
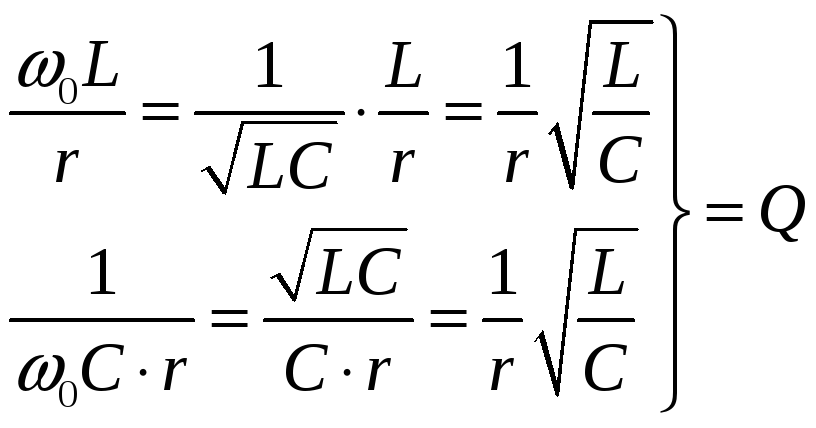
![]() -
добротность
-
добротность
Добротность- отношение сопротивления на реактивных элементах к активному в режиме резонанса.
![]()
 ,
где
,
где
![]()
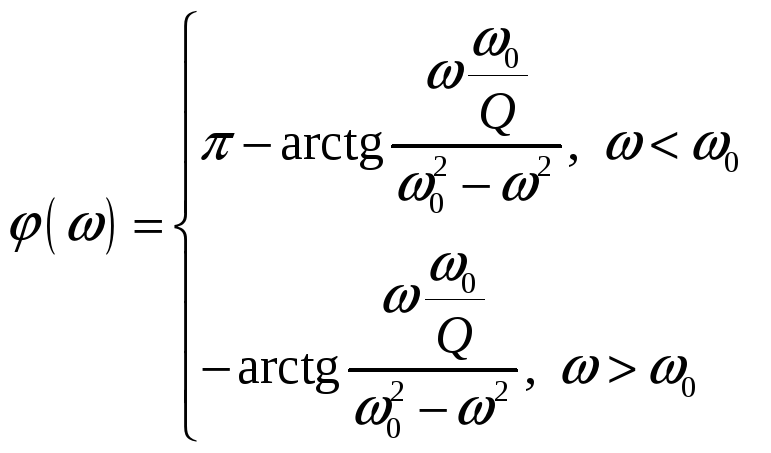
БИЛЕТ 20. Передаточная функция последовательной RLC-цепи.
а).
![]()

![]()
![]()
![]()

 .
.
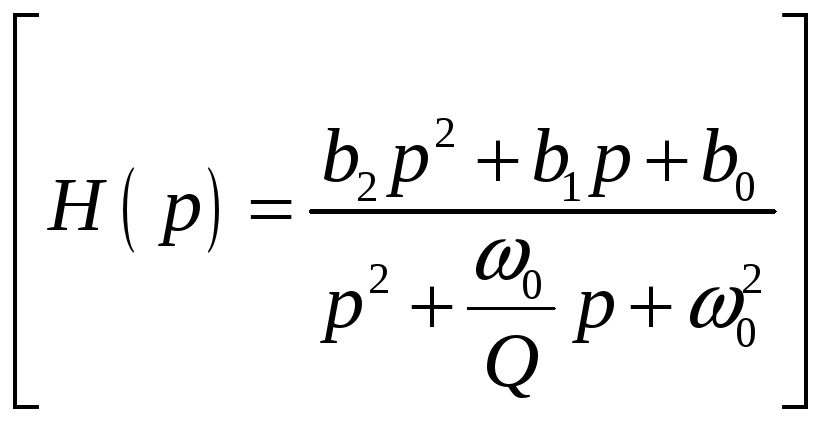 -
каноническая форма записи
-
каноническая форма записи
![]() для фильтра 2-го порядка.
для фильтра 2-го порядка.
![]() ,
,
![]()
![]() ,
,
![]()
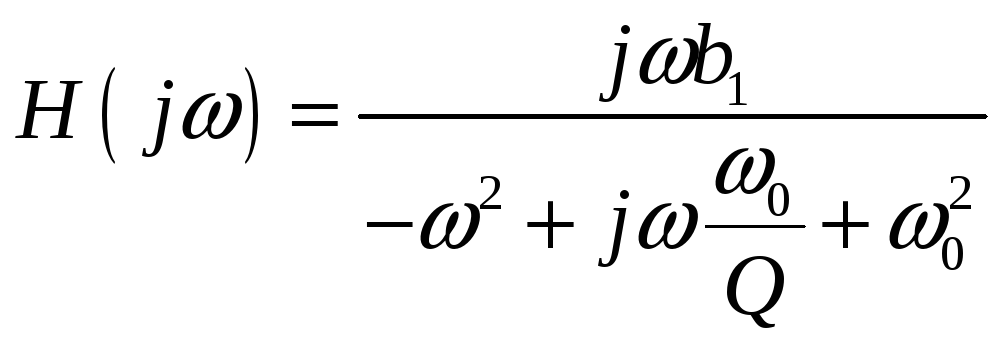
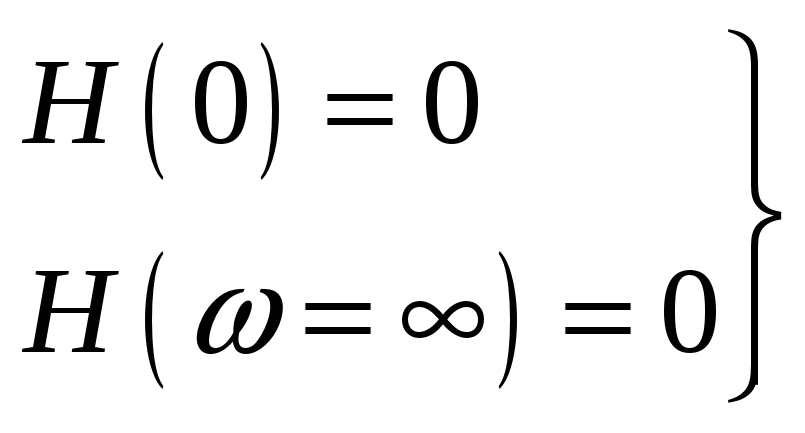
![]() ППФ
2-го порядка.
ППФ
2-го порядка.
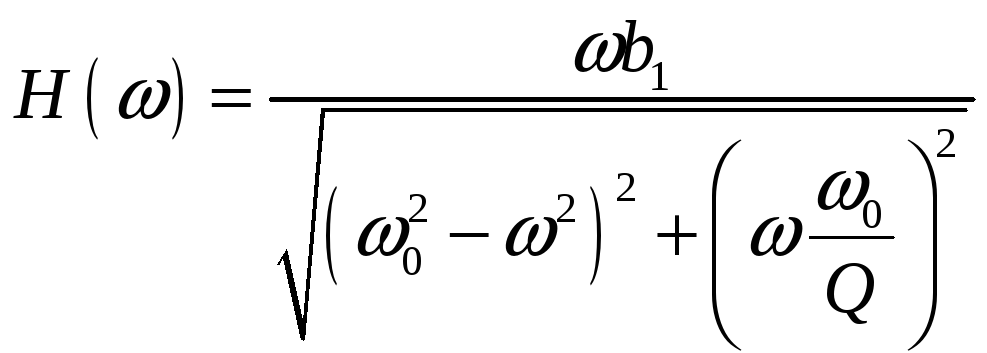

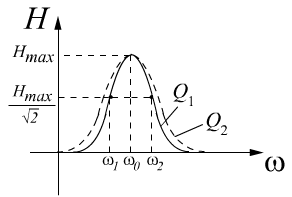
![]()
![]()
![]()
Чем шире полоса пропускания, тем меньше добротность, то есть хуже избирательное свойство цепи.
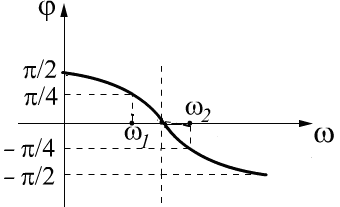
б).
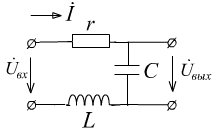
![]()
![]()
![]()
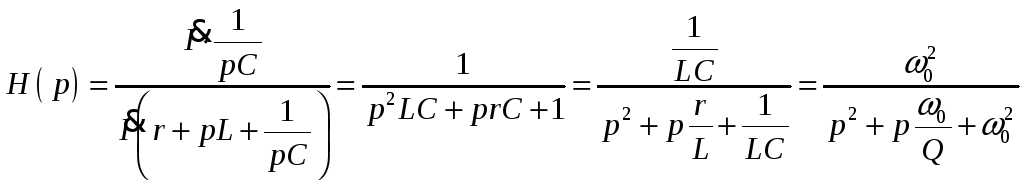 -
ФНЧ 2-го порядка.
-
ФНЧ 2-го порядка.




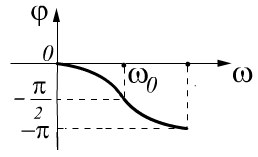
в).

![]()
![]()
![]()
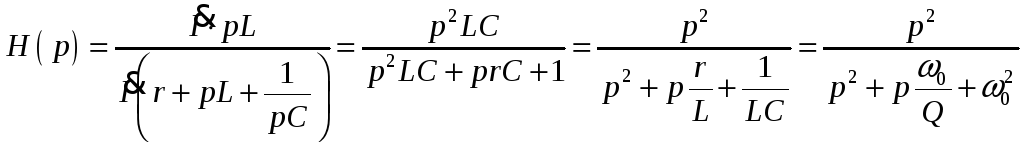

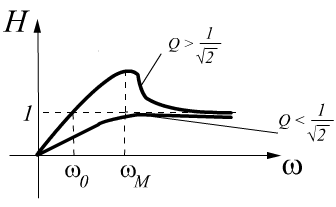 -
ФВЧ.
-
ФВЧ.
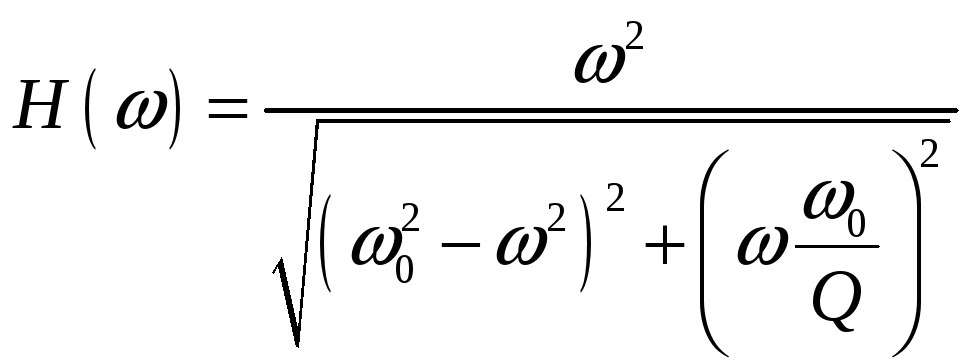
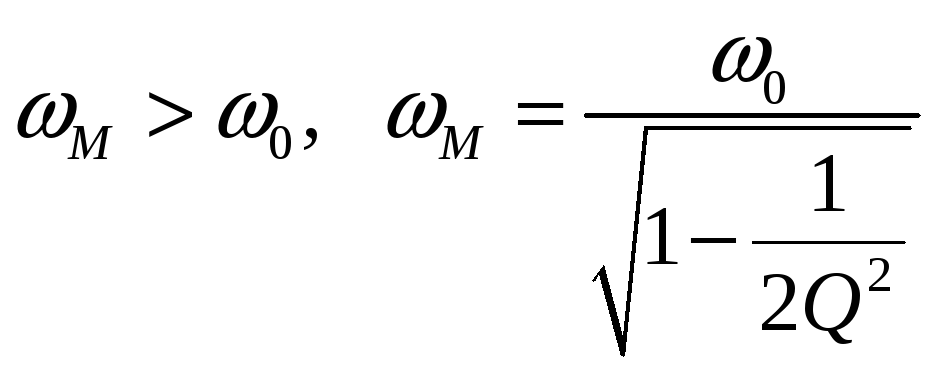

4).

- полосно-заграждающий фильтр

БИЛЕТ 21. Расчёт динамических режимов в линейной электрической цепи. Законы коммутации.
Подключение или отключение источников, элементов цепи и ветвей схемы называется коммутацией. При этом происходит изменение напряжений и токов на элементах, поэтому требуется время для достижения ими установившихся значений, то есть в цепи возникают переходные процессы.
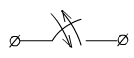
Вводится понятие идеального ключа.
![]() ,
,
![]() ,
,
![]()
![]() (время
непосредственно перед коммутацией).
(время
непосредственно перед коммутацией).
![]() (время
непосредственно после коммутацией).
(время
непосредственно после коммутацией).
![]()
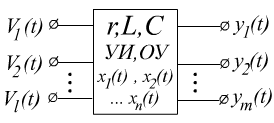
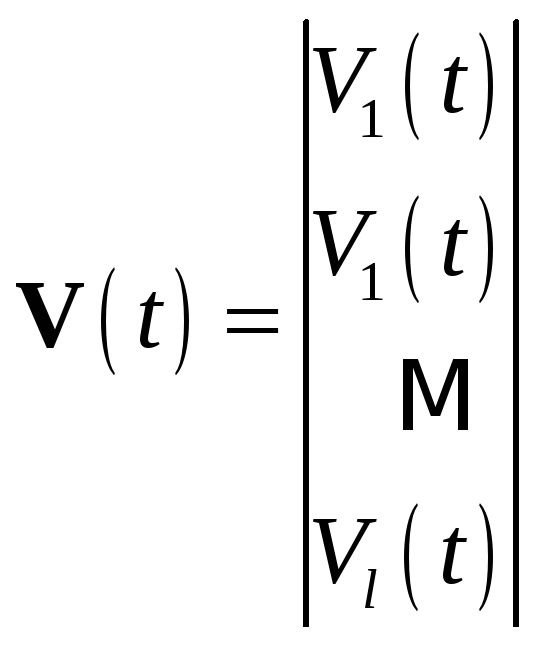
- матрица-столбец входных воздействий независимых источников тока и ЭДС
(внешние переменные).

- матрица-столбец выходных переменных.
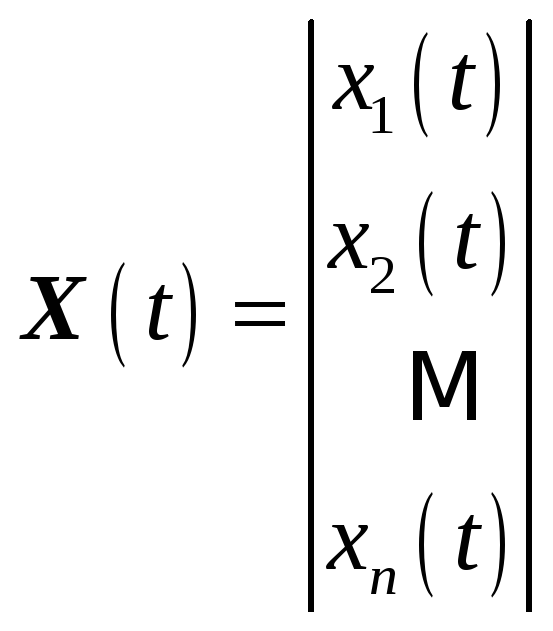
- матрица-столбец внутренних переменных или переменных состояния.
Замечание: в качестве переменных состояния используются напряжения на конденсаторах и токи на индуктивных элементах, так как эти элементы полностью определяют состояние цепи в любой момент времени.
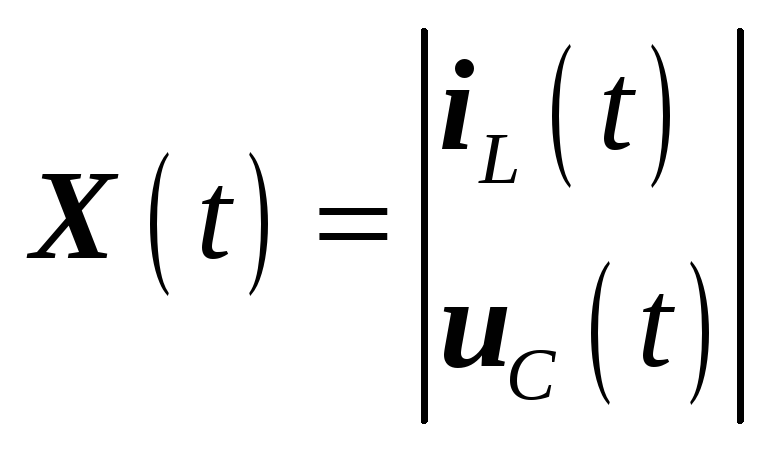
![]() ,
,
![]()
|
Компонентные уравнения |
Топологические уравнения |
|
|
|
Эти уравнения справедливы для любого момента времени и для любой цепи. Мы можем их преобразовать в дифференциальные уравнения первого порядка, которые называются матричными состояниями цепи или уравнениями состояния.
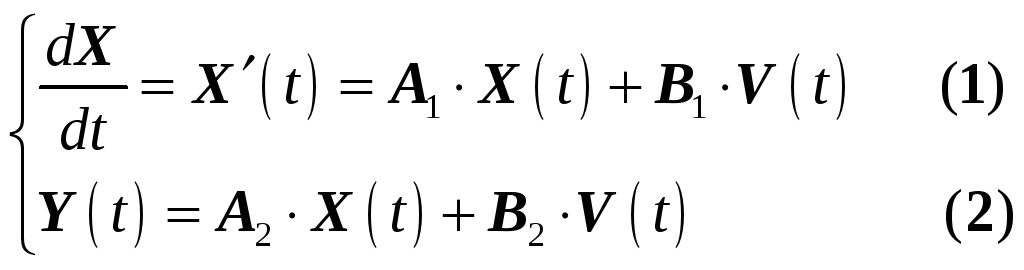 -
система
уравнений состояния.
-
система
уравнений состояния.
![]()
![]()
![]()
![]()
(Это матрицы вещественных коэффициентов, которые определяются параметрами схемы)
Уравнения
(1)
и (2)
– система
![]() линейных уравнений 1-го порядка.
линейных уравнений 1-го порядка.
Рассмотрим
решение дифференциального уравнения
![]() -го
порядка:
-го
порядка:
![]()
![]()
![]() -
характеристическое
уравнение.
-
характеристическое
уравнение.
Это
уравнение имеет
![]() корней.
корней.
Законы
коммутации.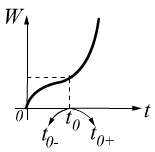
1.
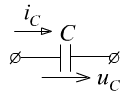
![]()
![]()
![]()
![]()
Для каждой конечной мощности источника сигнала энергия в любых элементах схемы не может изменяться мгновенно.

![]()
![]()

1-й закон коммутации:
![]() (напряжение
на конденсаторе не меняется скачком)
(напряжение
на конденсаторе не меняется скачком)
Можно
также записать:
![]()
2 .
.
![]()
![]()
![]()
Рассуждая аналогично, получаем:
2-й закон коммутации:
![]()
![]() (ток
на индуктивности не меняется скачком)
(ток
на индуктивности не меняется скачком)
Можно
также записать:
![]()
Замечание:
Иногда
![]()
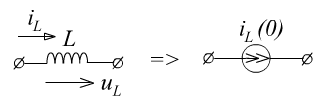
![]()
![]()

![]()
БИЛЕТ 22. Классический метод расчета переходных процессов в линейных цепях первого порядка (RC- и RL-цепи).