
- •Экзаменационная программа по курсу "Общая электротехника и электроника" (3 семестр, поток а-1, 2, 15-05)
- •Линейные электрические цепи со сосредоточенными параметрами. (постоянные)
- •Основные интегральные переменные.
- •Математические модели двухполюсных элементов электрической цепи (во временной области).
- •Основные подграфы.
- •Топологические матрицы.
- •Полная система уравнений цепи.
- •Уравнения Кирхгофа с записью источников в явном виде.
- •I. Принцип суперпозиции (метод наложения).
- •Определение коэффициентов метода наложения.
- •Способ расчёта цепи с помощью метода наложения.
- •II. Принцип компенсации.
- •Комплексная форма ряда Фурье.
- •Расширенный метод узловых потенциалов (расширенные узловые уравнения).
- •Передача мощности от активного двухполюсника к пассивному двухполюснику.
- •1). Последовательное соединение.
- •2). Параллельное соединение.
- •Операционный усилитель (оу).
- •Малосигнальная низкочастотная модель оу в линейном режиме.
- •Инвертирующий усилитель на базе оу.
- •Повторитель.
- •Частотные электрические фильтры.
- •Добротность контура.
- •Классический метод расчета переходных процессов в цепях 1-го порядка.
- •Классический метод расчета. Цепи 1-го порядка.
- •1. Схема в установившемся режиме до коммутации,
- •2. Схема после коммутации,
- •1). Линейность.
- •2). Преобразование Лапласа от производной.
- •3). Преобразование Лапласа от интеграла.
- •Решение уравнений состояния в операторной форме.
- •Схемное моделирование источников в виде функции .
- •Связь переходной и импульсной характеристик цепи с передаточной функцией цепи.
- •3. Метод дискретных линейных моделей.
Передача мощности от активного двухполюсника к пассивному двухполюснику.
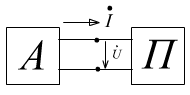
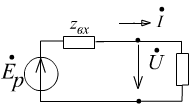
![]()
![]() .
.
![]() .
.

При
каком значении сопротивления
![]() в нём будет выделяться максимальная
активная мощность?
в нём будет выделяться максимальная
активная мощность?
1.
![]() ,
,
![]() ,
,
![]() 2.
2.
![]() ,
,
![]()
В
случаях 1 и 2 у нас выделяется![]()
![]()
![]()
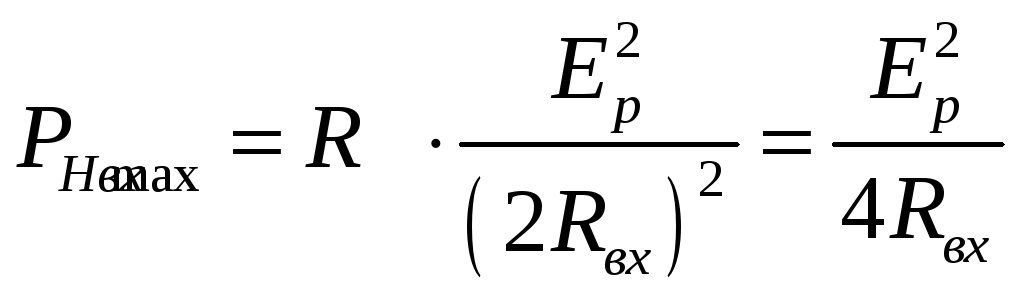
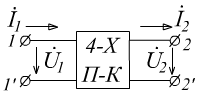
БИЛЕТ 14. Четырехполюсные элементы, их уравнения и матрицы типа Z, Y, Н, А. Определение коэффициентов уравнений четырехполюсников. Соединения четырехполюсников. Симметричные четырёхполюсники .
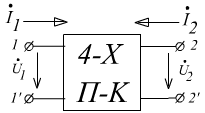
Зажимы
![]() -
первичные (или входные)
-
первичные (или входные)
Зажимы
![]() -
вторичные (или выходные)
-
вторичные (или выходные)
1.
Уравнение типа![]() :
:
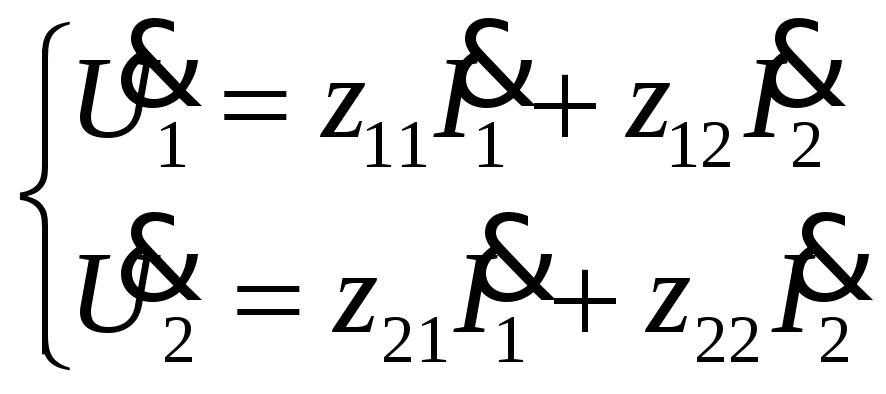
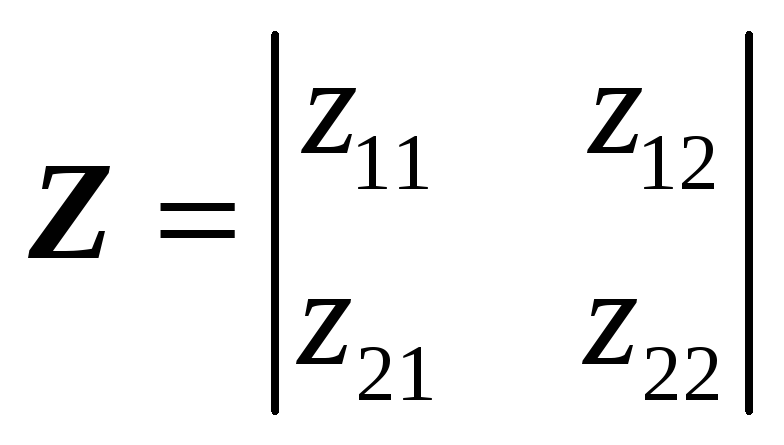
Чтобы
рассчитать все коэффициенты типа
![]() нужно рассмотреть режимы размыкания
(холостого хода) со стороны вторичных
и первичных зажимов.
нужно рассмотреть режимы размыкания
(холостого хода) со стороны вторичных
и первичных зажимов.
 -
входное сопротивление при разомкнутых
выходных зажимах.
-
входное сопротивление при разомкнутых
выходных зажимах.
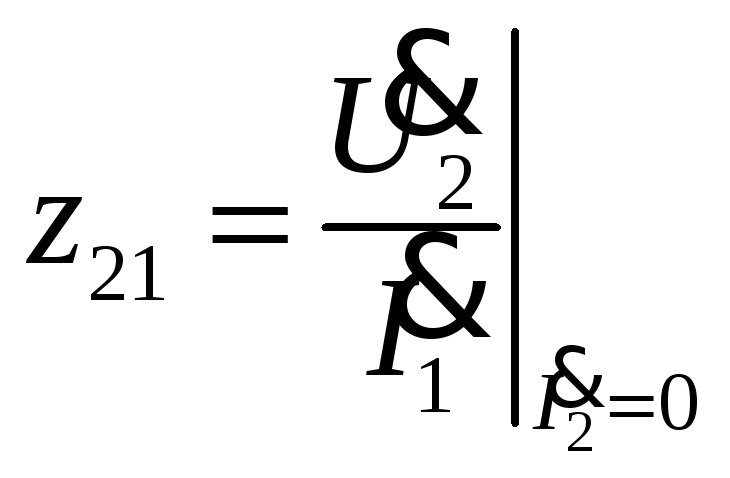 -
взаимное сопротивление при разомкнутых
выходных зажимах.
-
взаимное сопротивление при разомкнутых
выходных зажимах.
![]()
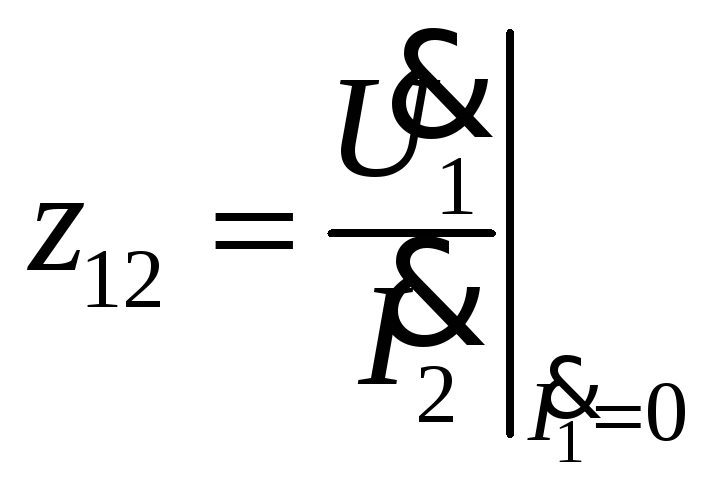
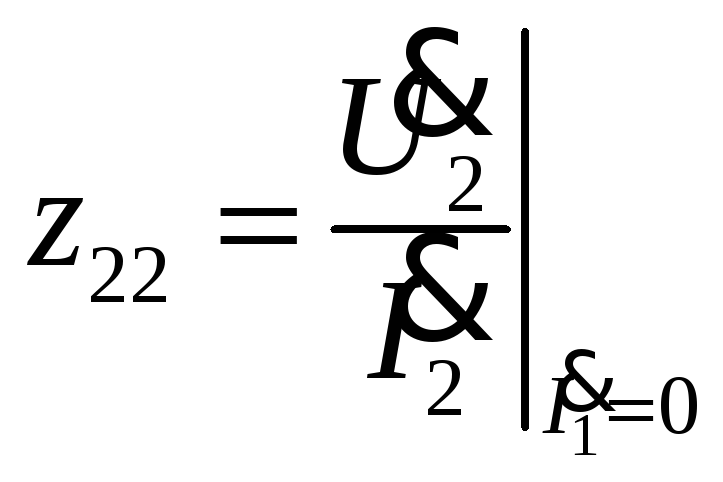 -
выходное сопротивление при разомкнутых
первичных зажимах.
-
выходное сопротивление при разомкнутых
первичных зажимах.
2.
Уравнения типа
![]() .
.
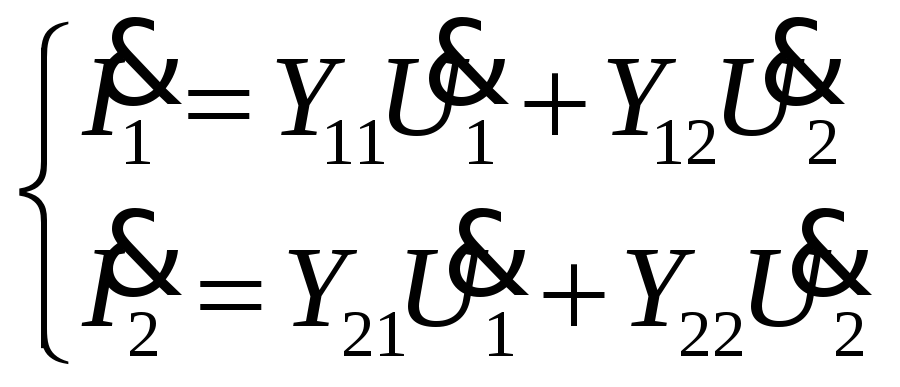
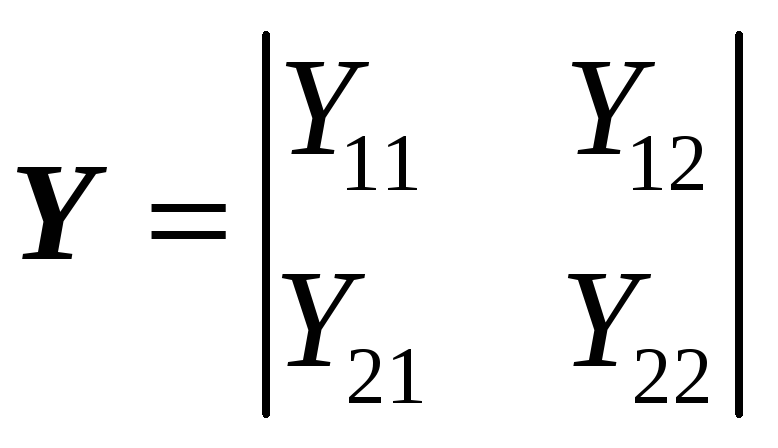 [См]
[См]
![]() -
параметры рассчитываются из схем
короткого замыкания со стороны первичных
и вторичных зажимов.
-
параметры рассчитываются из схем
короткого замыкания со стороны первичных
и вторичных зажимов.
3.
![]() -
параметры.
-
параметры.
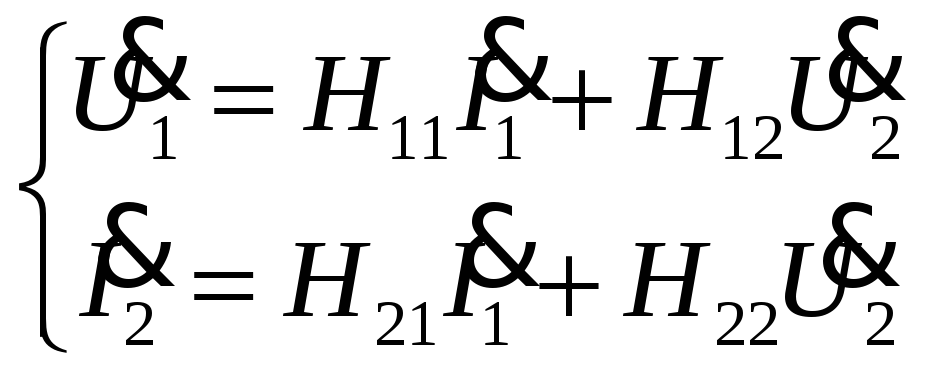
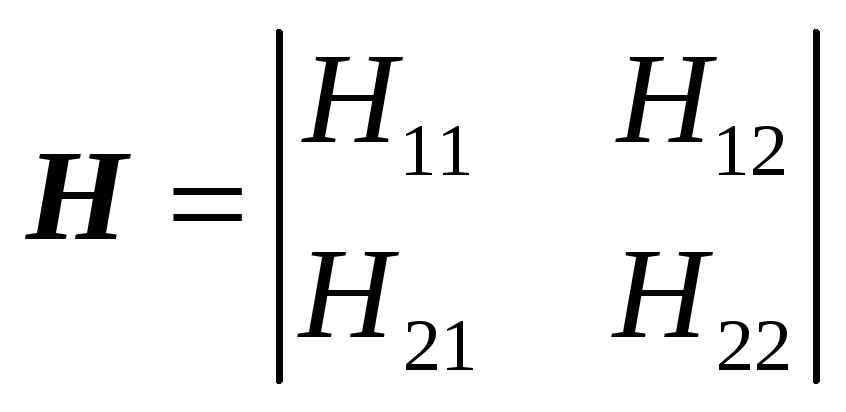
![]()

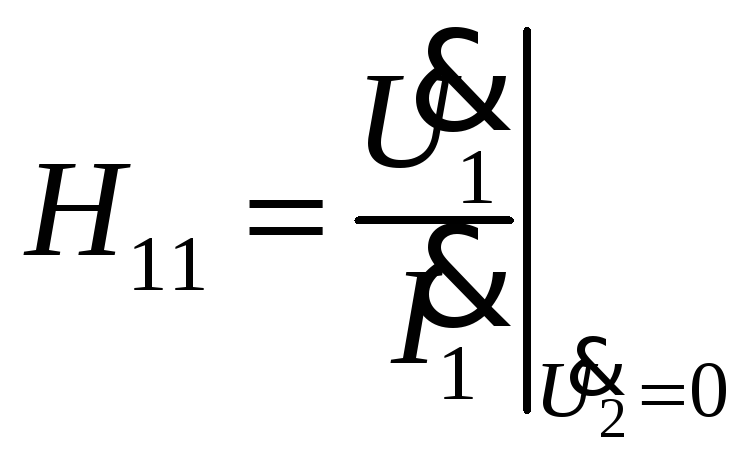 [Ом]-
входное сопротивление четырехполюсника
при замкнутых выходных зажимах.
[Ом]-
входное сопротивление четырехполюсника
при замкнутых выходных зажимах.
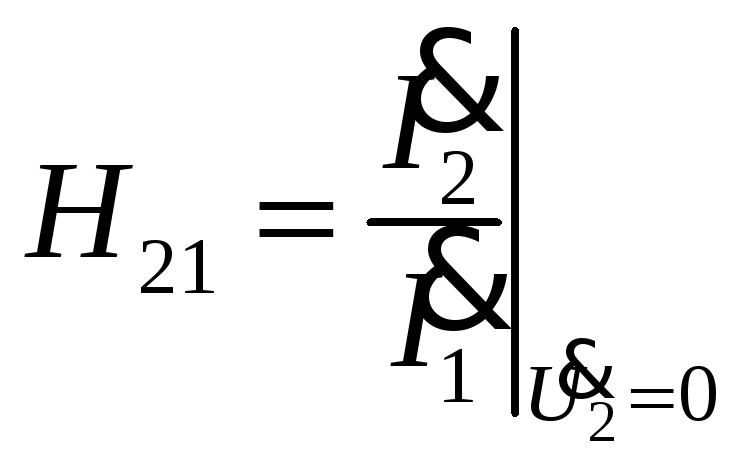 -
коэффициент передачи по току при
замкнутых вторичных зажимах.
-
коэффициент передачи по току при
замкнутых вторичных зажимах.
![]()
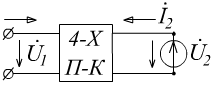
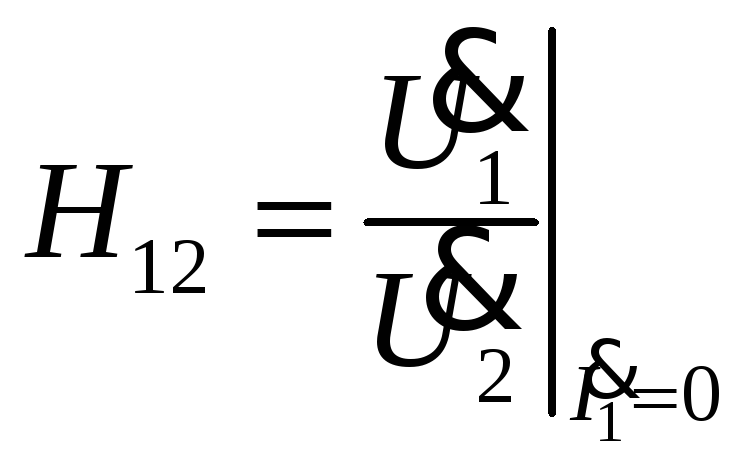 -
коэффициент передачи по напряжению при
разомкнутых первичных зажимах.
-
коэффициент передачи по напряжению при
разомкнутых первичных зажимах.
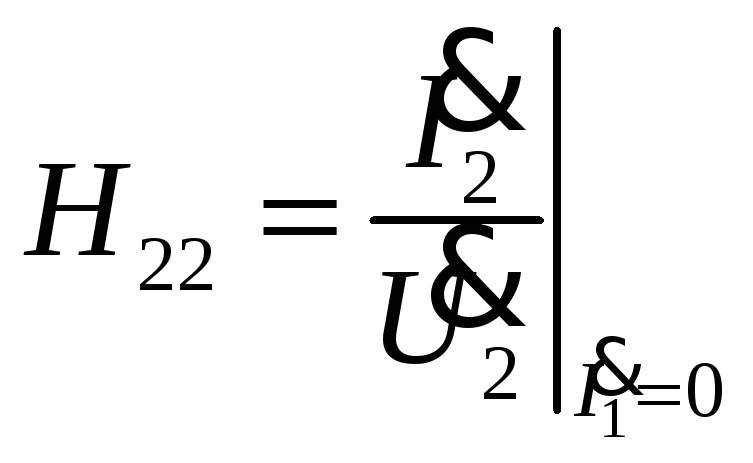 [См]-
выходная проводимость четырехполюсника
при разомкнутых первичных зажимах.
[См]-
выходная проводимость четырехполюсника
при разомкнутых первичных зажимах.
4.
![]() -
параметры.
-
параметры.
![]()
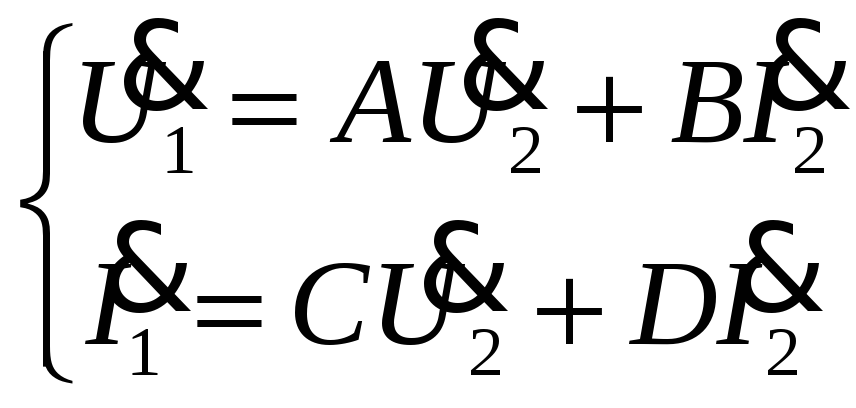
Параметры
типа
![]() определяются из схем короткого замыкания
и холостого хода выходных зажимов
четырёхполюсника.
определяются из схем короткого замыкания
и холостого хода выходных зажимов
четырёхполюсника.
Замечания:
1). Если внутри четырехполюсника есть источник (то есть у нас четырехполюсник является активным), то уравнения можно записать так:

2). Для пассивных линейных многополюсников выполняется условие взаимности:
![]() ,
,
![]() ,
,
![]()
![]()
3). Условие симметричности четырехполюсника:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
В общем случае четырёхполюсники имеют четыре независимых параметра. Взаимный четырехполюсник имеет три независимых параметра. Взаимно-симметричный четырехполюсник имеет два независимых параметра.
Симметричные четырехполюсники.

У данного взаимно-симметричного четырехполюсника можно поменять местами входные и выходные зажимы без какого-либо изменения условия передачи электроэнергии через него.
Пусть
четырехполюсник характеризуется
параметрами типа
![]() .
.
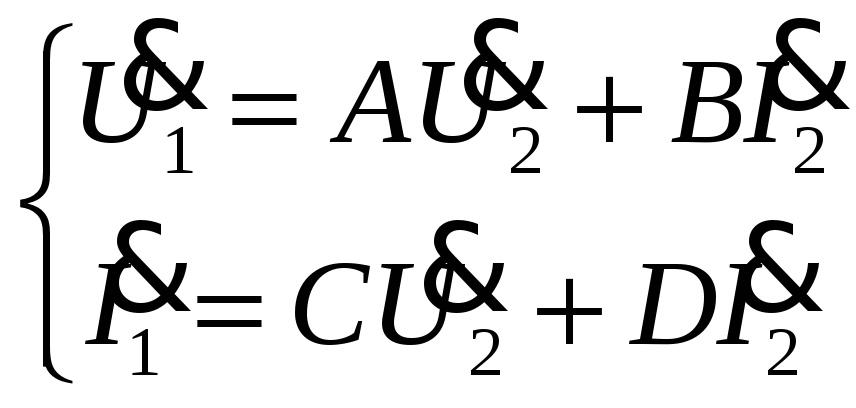 (1).
(1).
![]() ,
,
![]()
![]()
Соединения четырехполюсников.
1). Последовательное соединение.

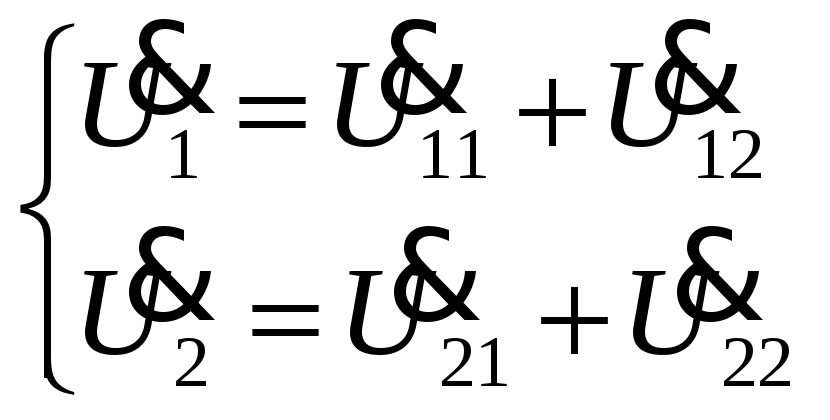
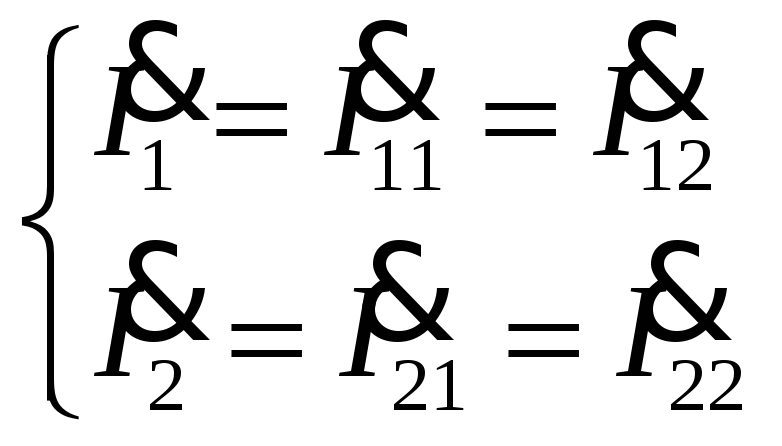
При
последовательном соединении
четырехполюсников матрицы
![]() складываются:
складываются:
![]()
Это справедливо для регулярного соединения четырехполюсников.
Если соединение регулярное, что при любой общей нагрузке токи, проходящие через оба первичных и оба вторичных зажима должны быть равны соответственно по величине и противоположны по направлению (для каждого четырехполюсника).
У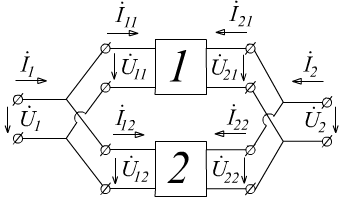 ниверсальный
способ регулярного соединения-
рассмотрение четырехполюсника как
ниверсальный
способ регулярного соединения-
рассмотрение четырехполюсника как
![]() -
полюсник.
-
полюсник.
