1). Линейность.

Если функция (является линейной комбинацией функций) и если для каждой функции существует преобразование Лапласа , тогда .

2). Преобразование Лапласа от производной.

Если , то , где - преобразование Лапласа.

.

3). Преобразование Лапласа от интеграла.

Если , то преобразование Лапласа: , где - преобразование Лапласа.

Таблица преобразований Лапласа:

Первые три преобразования в таблице используются в цепях 1-го порядка, последние 2 преобразования- в цепях 2-го порядка.

БИЛЕТ 27. Решение уравнений состояния в операторной форме. Расчёт переходных процессов с помощью операторной схемы замещения электрической цепи. Пример расчёта.

Расчет переходных процессов с помощью операторной схемы замещения.

Компонентное уравнение элементов цепи в операторной форме.

1.

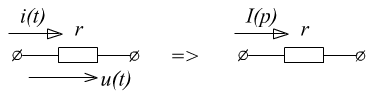
2.

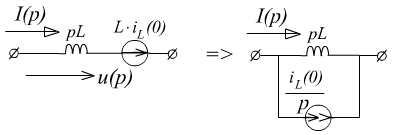
3.

4.

Для проведения расчетов в операторной схеме необходимо все уравнения (топологические, компонентные, узловые и т.д.) записать в операторной форме.

Решение уравнений состояния в операторной форме.

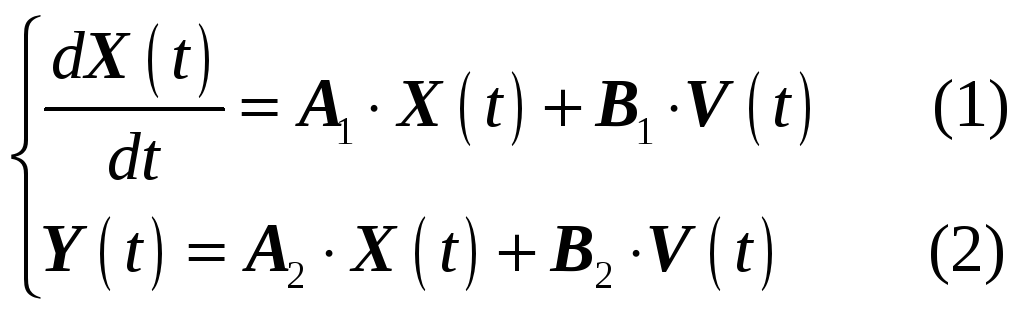
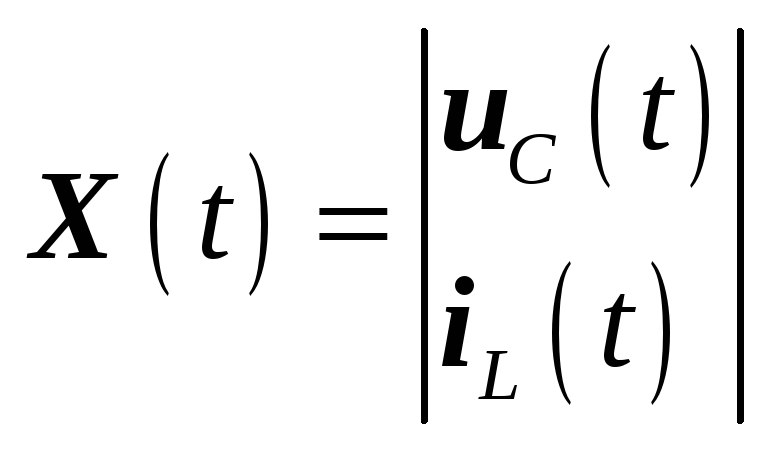
- обратное изображение нужно вычислять для каждого из элементов

Рассмотрим , (источников в схеме нет).

Тогда получим решение:

.

БИЛЕТ 28. Единичная функция и единичный импульс. Переходная и импульсная характеристика цепи.

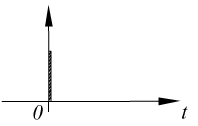
1. Единичная функция

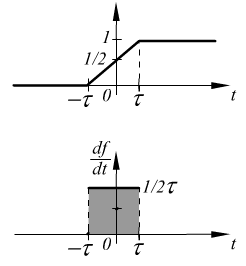
2. Единичный импульс

или

Схемное моделирование источников в виде функции .

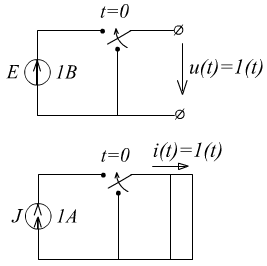
Замечание:

(- преобразование Лапласа).

Переходная характеристика- реакция цепи (отклик) на воздействие в виде единичной функции при ННУ .

Импульсная характеристика- реакция цепи на воздействие в виде единичного импульса при ННУ .

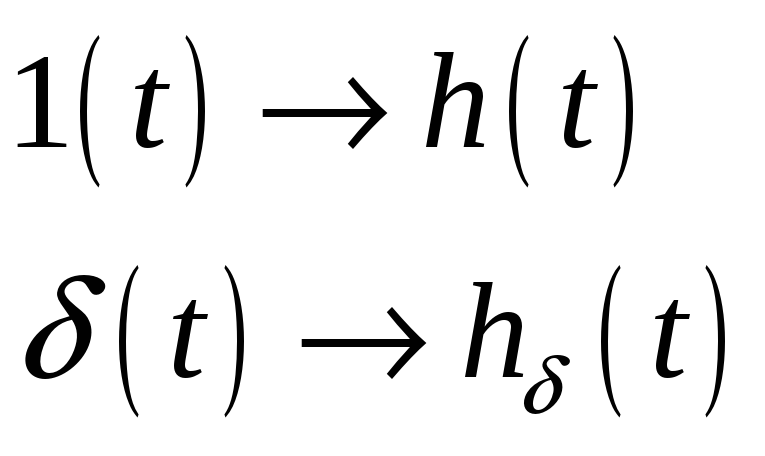
, - временные характеристики цепи.

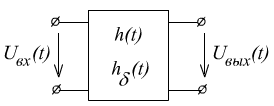
БИЛЕТ 29. Вывод соотношения для расчёта динамических режимов при произвольном воздействии (инте­грал Дюамеля). Связь переходной и импульсной характеристики цепи с передаточной функци­ей цепи.

Так как нас интересует момент времени .

С другой стороны:

(считаем, что воздействие начинается при ).

Этот интеграл называется интегралом Дюамеля (свертка и ).