
- •6.170103 "Управління інформаційною безпекою"
- •Задача Коші
- •Метод Ейлера
- •Модифікований метод Ейлера
- •Метод Рунге – Кутта четвертого порядку
- •Методи з автоматичною зміною кроку
- •Метод Рунге-Кутта з автоматичною зміною кроку
- •Метод Рунге-Кутта-Мерсона з автоматичною зміною кроку
- •Метод Рунге-Кутта-Фельберга з автоматичною зміною кроку
- •Методи прогнозу і корекції
- •Метод Мілна
- •Метод Адамса
- •Метод Хемінга
- •Формула корекції
- •2.Завдання до лабораторної роботи
- •2.1. Домашня підготовка до роботи
- •2.2. Робота в лабораторії
- •Контрольні запитання
- •Список літератури
- •Методи чисельного розв’язування
- •"Комп’ютерні методи дослідження інформаційних процесів та систем"
- •6.170103 "Управління інформаційною безпекою"
МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ "ЛЬВІВСЬКА ПОЛІТЕХНІКА"
МЕТОДИ ЧИСЕЛЬНОГО РОЗВ’ЯЗУВАННЯ
диференціАЛЬНИХ рівнянь
Методичні вказівки
до лабораторної роботи № 6
з курсу
"Комп’ютерні методи дослідження інформаційних процесів та систем"
для студентів базових напрямів 6.170101 "Безпека інформаційних і комунікаційних систем", 6.170102 "Системи технічного захисту інформації",
6.170103 "Управління інформаційною безпекою"
Затверджено
на засіданні кафедри
«Безпека інформаційних
технологій»
Протокол № 12 від 12.05.2011р.
Львів – 2011
Методи чисельного розв’язування диференціальних рівнянь: Методичні вказівки до лабораторної роботи №6 з курсу "Комп’ютерні методи дослідження інформаційних процесів та систем" для студентів базових напрямів 6.170101 "Безпека інформаційних і комунікаційних систем", 6.170102 "Системи технічного захисту інформації", 6.170103 "Управління інформаційною безпекою" / Укл.: Л.В. Мороз, А.Я. Горпенюк, Н.М. Лужецька - Львів: Видавництво НУ“ЛП”, 2011..- 14 с.
Укладачі: Л.В. Мороз, к.т.н., доц.
А.Я. Горпенюк, к.т.н., доц.
Н.М. Лужецька, асист.
Відповідальний за випуск: В.М. Максимович, д.т.н., проф.
Рецензент: В.В. Хома, д.т.н., проф.
А.Е. Лагун, к.т.н., доц.,
Мета роботи – ознайомлення з методами чисельного розв’язування диференційних рівнянь.
ВСТУП
Диференціальне рівняння (ДР), що містить лише одну незалежну змінну і похідні за нею, називають звичайними (ДР). ДР, що містить декілька незалежних змінних і похідні за ними, називають рівняння в частинних похідних.
Порядком
ДР називається найвищий порядок похідної
(або диференціалу), який входить в
рівняння. Звичайне ДР (ЗДР)
![]() -го
порядку в загальному випадку має
незалежну змінну, невідому функцію та
її похідні до
-го
порядку в загальному випадку має
незалежну змінну, невідому функцію та
її похідні до
![]() -го
порядку включно:
-го
порядку включно:
![]() (1)
(1)
![]() - незалежна
змінна;
- незалежна
змінна;
![]() -
невідома функція (залежна змінна);
-
невідома функція (залежна змінна);
![]() -
похідні цієї функції.
-
похідні цієї функції.
Диференціальне
рівняння
![]() -го
порядку, розв’язане відносно старшої
похідної, може бути записано у вигляді:
-го
порядку, розв’язане відносно старшої
похідної, може бути записано у вигляді:
![]() (2)
(2)
Щоб розв’язати ЗДР, необхідно мати значення залежної змінної та (або) її похідних при деяких значення незалежної змінної.
Якщо ці
значення задані при одному значенні
незалежної змінної - така задача
називається задачею з початковими
умовами або задачею Коші, а при
![]() або більше значеннях незалежної змінної
- задача називається крайовою.
або більше значеннях незалежної змінної
- задача називається крайовою.
Значення залежної змінної та її похідних називаються додатковими умовами, котрі в задачі Коші називаються початковими, а в крайовій задачі - граничними.
Задача Коші
Задача Коші формулюється так:
Нехай задане ДР
![]() (3)
(3)
з
початковими умовами
![]() .
Потрібно знайти функцію
.
Потрібно знайти функцію
![]() ,
що задовольняє дане рівняння та початкову
умову. Для одержання чисельний розв’язку
цієї задачі спочатку обчислюють значення
похідної, а потім задаючи малий приріст,
переходять до нової точки
,
що задовольняє дане рівняння та початкову
умову. Для одержання чисельний розв’язку
цієї задачі спочатку обчислюють значення
похідної, а потім задаючи малий приріст,
переходять до нової точки
![]()
Положення
нової точки визначають за нахилом
кривої, обчисленому з допомогою ДР.
Таким чином, графік чисельного розв’язку
являє собою послідовність коротких
прямолінійних відрізків, якими
апроксимується істинна крива
![]() .
Сам чисельний метод визначає порядок
дій при переході від даної точки кривої
до наступної.
.
Сам чисельний метод визначає порядок
дій при переході від даної точки кривої
до наступної.
Існують дві групи методів розв’язування задачі Коші.
-
Однокрокові методи. В них для знаходження наступної точки на кривій
 потрібна інформація лише про попередній
крок.
потрібна інформація лише про попередній
крок.
-
Багатокрокові. Для знаходження наступної точки кривої
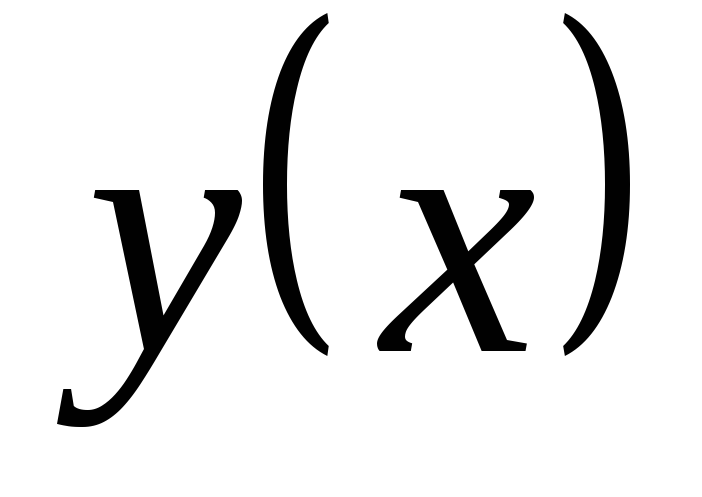 вимагається інформація більш ніж про
одну з попередніх точок.
вимагається інформація більш ніж про
одну з попередніх точок.
Всі ці методи розв’язування ДР дають розв’язок у вигляді таблиці значень.
