46. Метод моментов.
Пусть з-н распределения интервальной
совокупности Х известен с точностью до
параметров
.
Выберем m каких-либо
начальных и центральных моментов
,
найдем теоретически их зависимость от
и приравняем эти зависимости к
соответствующим выборочным моментам
Получим систему m уравнений, для нахождения оценок:
Пример. Пусть
(равномерное
распределение)
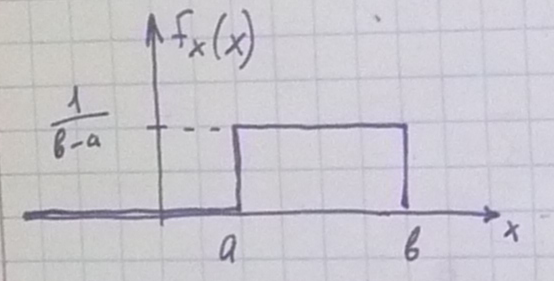
Найти ММ оценки параметров а и b :
Находим:
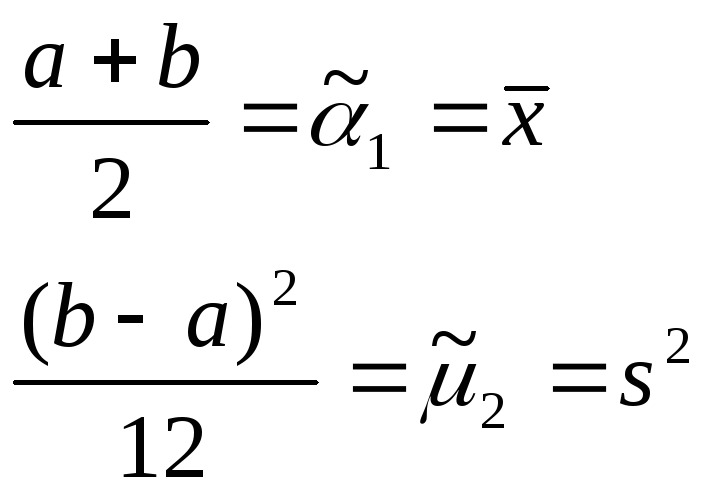
Общее: и для 47 и 48:
Пусть неизвестная функция генеральной
совокупности зависит от некоторого
параметра
.
Нужно по наблюдениям оценить параметр.
Для построения оценок используются
статистики – функции от выборочных
значений.
Примеры статистик.
.
Эта оценка
.
Будет рассматриваться, как приближенное
значение параметра
.Замечание.
Как правило, для оценки параметра
можно использовать несколько статистик,
получая при этом различные значения
параметра
.
Как измерить «близость» оценки
к истинному значению
?
Как определить качество оценки?
Комментарий: Качество оценки
определяется не по одной конкретной
выборке, а по всему мыслимому набору
конкретных выборок, т.е. по случайному
выборочному вектору
,
поэтому для установления качества
полученных оценок моментов
,
следует во всех этих формулах заменить
конкретные выборочные значения
на СВ Xi.
;
;
.
Качество оценки устанавливают, проверяя, выполняются ли следующие три свойства (требования).Требования, предъявляемые к точечным оценкам:
1. Несмещенность, т.е.
.
Это свойство желательно, но не обязательно. Часто полученная оценка бывает существенной, но ее можно поправить так, что она станет несмещенной.
Иногда оценка бывает смещенной, но
асимптотически несмещенной, т.е.
.
2. Состоятельность, т.е.
.
Это свойство является обязательным. Несостоятельные оценки не используются.
3. Эффективность.
а) Если оценки
и
– несмещенные, то
и
.
Если
,
то оценка
более эффективна, чем
.
б) Если оценки
и
– смещенные, тогда
и
.
Если
,
то оценка
более эффективная, чем
.
Где
– средний квадрат отклонения оценки.
Рассмотрим использование этих свойств на примерах выбора оценок МО и дисперсии:
47. Выборочная дисперсия Докажем,
что выборочная дисперсия является
смещенной оценкой для дисперсии
генеральной совокупности.
Выполним следующие преобразования
;
.
Найдем МО для дисперсии:
.
.
МО не совпадает с 2, а отличается на –2/n – смещение. Таким образом эта оценка занимает в среднем истинное значение дисперсии на величину 2/n, правда это смещение сходит на нет при n .
Чтобы устранить это смещение надо «исправить» дисперсию.
;
;
.
Можно доказать, что статистика S2 является и состоятельной оценкой для дисперсии генеральной совокупности.Замечание. К сожалению, на практике при оценке параметров не всегда оказывается возможным одновременное выполнение требований: несмещенности, эффективности и состоятельности.
48. Выборочное среднее:
является несмещенной и состоятельной
оценкой МО генеральной совокупности
(X1 ,…,
Xn
), причем каждое Xi
совпадает с m и
2.
а)
Несмещенность.
По определению выборочного вектора
,
причем Xi
– независимые в совокупности СВ,
тогда вычислим
M[Xсред]=M[(1/n)Xi]=(1/n)M[Xi]=
(1/n)M[Xi]=(1/n)nm
.
D[Xсред]=D[(1/n)Xi]=(1/n2)D[Xi]=
(1/n2)D[Xi]=(1/n)n2=2/n
б) Состоятельность Воспользуемся
неравенством Чебышева:
Применим это неравенство к
При n
,что
и доказывает состоятельность
.