5. Интервальные оценки

Теоретические основы.

Пусть – случайная выборка, распределение ко­то­рой F_(x) зависит от некоторого неизвестного параметра . Интервал с границами , зависящими от выбороч­ных данных, на­­зы­вается

(1-)-до­­ве­­­ри­тель­ным интервалом для параметра , если

.

(*)

Статистика называется

верхней (1-)-дове­рительной границей для па­ра­метра , если

.

Статистика называется

нижней (1-)-дове­рительной границей для па­ра­метра , если

.

Интерпретация.

Смысл этих определений легко понять, если вспомнить, что индекс , стоящий у знака вероятности , указывает на истинное значение неизвестного параметра. Поэтому формула (*), например, означает, что с большой вероятностью доверительный интервал накроет ис­тинное значение оце­ни­ва­е­мого па­ра­метра. На практике обычно де­лается несколько вольный вывод, что с большой долей вероятности следует ожидать зна­че­ние оце­ни­ва­е­мого параметра, принадлежащее интервалу . В таком утверждении “скрытно” присутствует предположение о случайности изменения параметра от эксперимента к эксперименту. В дей­ст­ви­тель­ности, оцениваемый параметр не случаен, а имеет некоторое фиксированное неизвестное значение.

Точность и надежность интервала.

Величина Q = (1-)·100% называется надежностью интервала и вы­би­ра­ет­ся обычно в пределах от 90% до 99% (стандартное значение – 95%). На первый взгляд кажется, что чем выше значение надежности, тем лучше будет построенный интервал. Однако здесь надо учитывать, что чем больше величина Q, тем шире получится доверительный интервал (в пределе при он будет совпадать с ), то есть уменьшится его точность. Задача построения доверительного интервала с заданной точностью и надежностью может быть решена только при достаточно большом объеме выборки.

Двухсторонний интервал через доверительные границы.

Для построения (1-)-дове­ри­те­ль­ного интервала можно построить отдельно верхнюю и нижнюю границы с надежностью (1-/2)·100%.

Связь с задачей проверки гипотез.

Пусть – некое (1-)-довери­тель­ное множество. Тогда критерий, отвергающий гипотезу, если полностью попадает в область альтернативы, будет иметь уровень . Так, при альтернативе ги­по­те­зу следует отвергать, если нижняя граница . Если же ошибочно принимать гипотезу, когда доверительное множество полностью по­па­да­ет в область гипотезы (нап­­ри­мер, верхняя граница ), то такой критерий будет иметь вовсе “неприемлемый” уровень 1-, вместо ожидаемого уровня .

Обратно, рассмотрим задачу проверки простой ги­по­те­зы о параметре рас­пре­­деления наблюдаемой случайной величины. Пусть – крити­чес­кая об­­ласть уровня  (область, где гипотеза отвергается). Тогда множество B(x⁽ⁿ⁾) тех значений параметра , при которых гипотеза принимается, –

,

образует (1-)-доверительное множество. Множество определяет

1. нижнюю грани­цу, если альтер­на­ти­ва имеет вид ;

2. верхнюю грани­цу, если альтер­на­ти­ва имеет вид ;

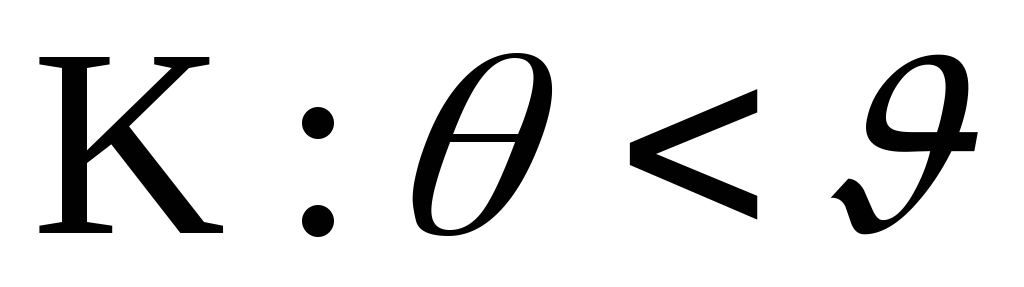3. двухсторонний интервал, для альтер­на­ти­вы вида .