Задание 6. Критерий знаков.

Постановка задачи.

Двухвыборочный вариант. Имеются две выборки одинакового объема. Известно, что каждое -ое наблюдение в 1-ой выборке зависит (в вероятностном смысле) от соответствующего -ого наблюдения во второй выборке. Распределение выборок неизвестно. Требуется проверить гипотезу однородности выборок.

Одновыборочный вариант. Имеется одна выборка. Требуется проверить гипотезу, что некоторое фиксированное событие происходит чаще, чем противоположное к этому событию утверждение (например, лечение чаще приводит к выздоровлению).

Теоретические основы.

Если исследователя интересует лишь факт наличия эффекта воздействия и нет оснований предполагать нормальность распределения выборок, то можно каждую пару исходных данных заменить величиной , принимающей всего два значения: , если эффект есть, и , если эффекта нет. Под эффектом может пониматься, например, уменьшение артериального давления после лечения или увеличение доли полезных веществ после стерилизации. Если предположить, что воздействие не обладает никаким эффектом, то величина будет иметь распределение Бернулли с вероятностью успеха p = 0,5 (– приблизительно в 50% случаев должен наблюдаться эффект). Исследователю было бы интересно проверить гипотезу

– эффект отсутствует или направлен противоположно, при альтернативе .

Для проверки гипотез подобного рода можно использовать критерий знаков, статистика которого M равна числу благоприятных исходов:

.

Из определения видно, что M имеет биномиальное распределение с параметрами (n, p). Нулевая гипотеза должна отвергаться, если выборочное значение m статистики M будет достаточно большим. Критический уровень значимости такого критерия равен (по формуле для биномиального распределения)

.

Нетрудно понять, что supremum в последнем выражении достигается на границе между гипотезами при p = 0,5 (чем больше , тем больше ожидаемое значение ). Таким образом, при выборочном значении

.

(*)

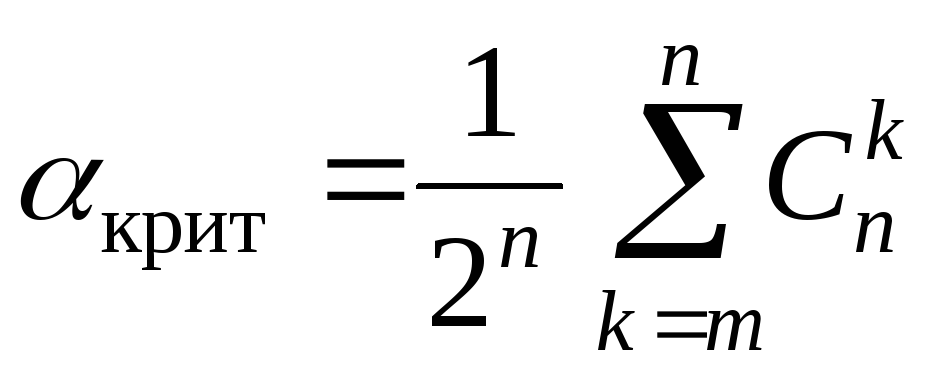Замечание. Описанную схему можно применять также для проверки гипотезы о вероятности “успеха” при биномиальных испытаниях – одновыборочный вариант критерия. В качестве примера рассмотрим ситуацию, когда при составлении договора купли-продажи заказчиком была оговорена нижняя граница в 92% для доли доброкачественной продукции. При поступлении товара заказчик проводит контрольные измерения n единиц продукции. По результатам испытаний, основываясь только на количестве кондиционной продукции, требуется проверить гипотезу (опять же гипотеза противоположна ожиданиям).

Другой пример. С целью прогнозирования результатов будущих выборов было опрошено 1000 респондентов. Среди них оказалось 35 сторонников партии «Будет ещё хуже!». Можно ли утверждать, что эта партия не попадет в думу?

Если считать 1000 респондентов каплей в море всех избирателей и отбор респондентов производился абсолютно случайно, то можно описать наши наблюдения как выборку из распределения Бернулли с вероятностью успеха , равной доле всех сторонников указанной партии. Если мы находимся на позициях противников партии «Будет ещё хуже!», мы хотели бы, что бы эта доля была меньше 0,05. Поэтому в качестве альтернативы мы должны выбрать утверждение .

Итак, , граничное значение . Критический уровень значимости равен .

Вывод. Скорее всего (с надежностью 98,6%), партия «Будет ещё хуже!» не пройдет в Думу.