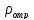- •1. Основные характеристики реактора и исходные данные для расчета.
- •2. Определение геометрических параметров ячейки.
- •Определение размеров расчетной модели элементарной ячейки.
- •Определение ядерных концентраций компонентов топлива в ячейке.
- •5.Определение числа ядер компонентов топлива:
- •6. Подготовка констант.
- •6.1. Макросечения первой энергетической группы:
- •6.2. Макросечения второй энергетической группы:
- •6.3. Макросечения третьей энергетической группы:
- •7. Расчет микросечений третьей группы
- •8. Гомогенизация ячейки.
- •9. Сечения рассеяния четвертой энергетической группы.
- •10. Нахождение средних потоков.
- •11. Средние по ячейке сечения.
- •12. Расчет коэффициента размножения в бесконечной среде:
- •13. Одногрупповые константы
- •13.1. Коэффициент диффузии в активной зоне.
- •13.2. Коэффициент диффузии в отражателе:
- •14. Определение эффективного коэффициента размножения.
12. Расчет коэффициента размножения в бесконечной среде:
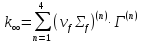
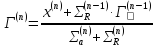
|
|
|
|
|
|
1 |
0,752 |
8,34 |
0,0043 |
|
2 |
0,248 |
10,4 |
0,0005 |
|
3 |
0 |
7,35 |
0,0119 |
|
4 |
0 |
17,3 |
0,0677 |
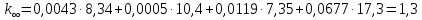
13. Одногрупповые константы
13.1. Коэффициент диффузии в активной зоне.
В уран – водных решетках возникают различия в свойствах среды в направлениях, параллельном и перпендикулярном топливным блокам.
Определяем коэффициенты диффузии в зонах ячейки:
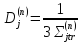
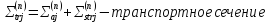
Рассчитываем
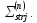
Первая энергетическая группа:
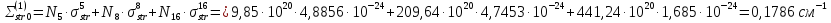
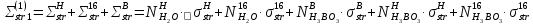 =
=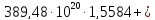 194,74
194,74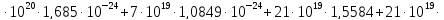 1,685
1,685 =0,0943
=0,0943
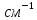
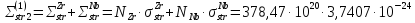 +
+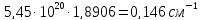
Вторая энергетическая группа:
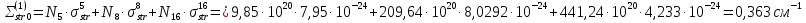
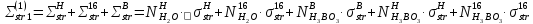 =
=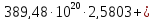 194,74
194,74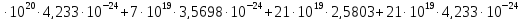 =
=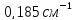
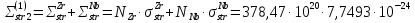 +
+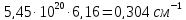
Третья энергетическая группа:
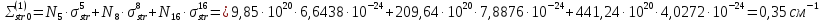
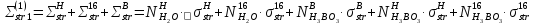 =
=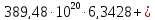 194,74
194,74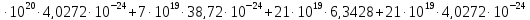 =
=
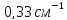
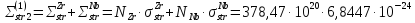 +
+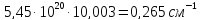
Четвертая энергетическая группа:
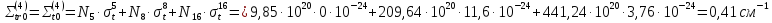
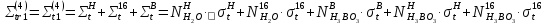 =
=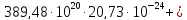 194,74
194,74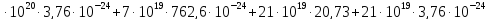 =
=
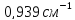
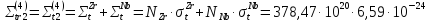 +
+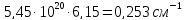
Находим
транспортное сечение
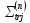 :
:
Первая энергетическая группа:
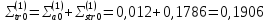
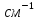
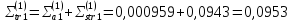
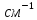
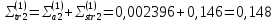
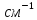
Вторая энергетическая группа:
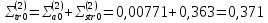
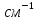
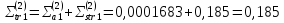
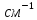
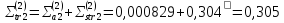
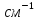
Третья энергетическая группа:
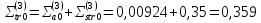
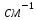
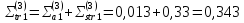
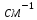
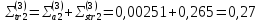
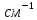
Определяем коэффициенты диффузии в зонах ячейки:
Первая группа:
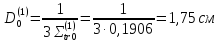
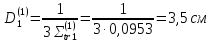
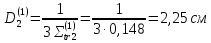
Вторая группа:
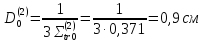
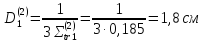
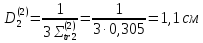
Третья группа:
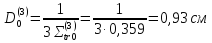
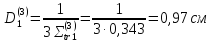
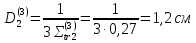
Четвертая группа:
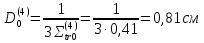
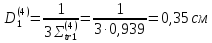
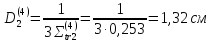
Коэффициенты диффузии вдоль ТВЭЛов (1,2,3 энергетическин группы) рассчитываются следующим образом:
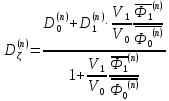
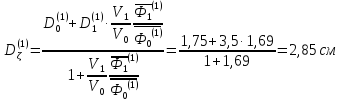
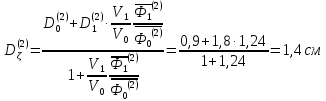
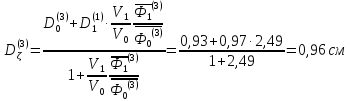
Для четвертой группы:
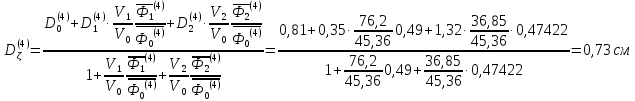
Коэффициенты диффузии в перпендикулярном направлении:
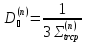
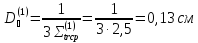
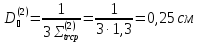
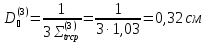
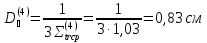
Полный коэффициент диффузии рассчитывается следующим образом:
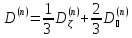
Первая группа:
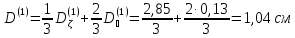
Вторая группа:
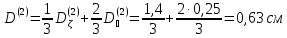
Третья группа:
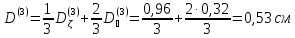
Четвертая группа:
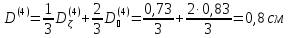
Коэффициент диффузии активной зоны находим следующим образом:
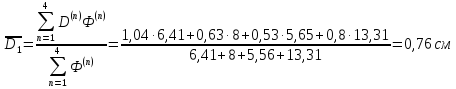
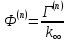
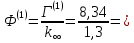 6,41
6,41
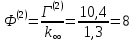
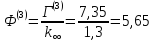
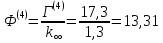
Площадь миграции активной зоны:

13.2. Коэффициент диффузии в отражателе:
Будем рассматривать отражатель как гомогенную смесь стали и воды,
поэтому все константы, ему соответствующие, рассчитываются с учетом весов объемов стали и воды.
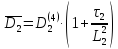
Т.к. я не поняла, как считается коэффициент диффузии в отражателе, то определение эффективного коэффициента размножения будет производиться, из условия критичности реактора.
14. Определение эффективного коэффициента размножения.
Условие критичности реактора:
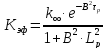
где
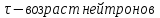 :
:
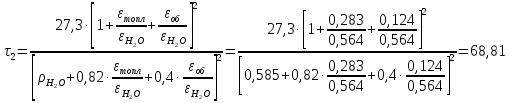
Квадрат
длины диффузии нейтронов в решетке –
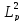 :
:
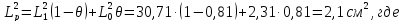
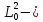 квадрат
длины диффузии в топливе:
квадрат
длины диффузии в топливе:
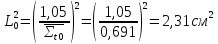
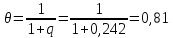
- коэффициент использования тепловых нейтронов.
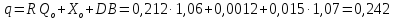
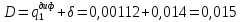
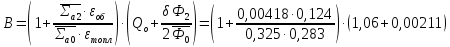
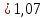
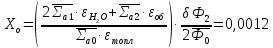
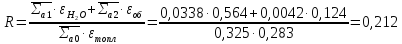
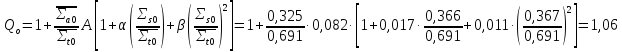
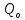 – коэффициент
внутренней экранировки, учитывающий
анизотропию после столкновений.
– коэффициент
внутренней экранировки, учитывающий
анизотропию после столкновений.
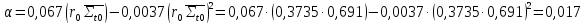
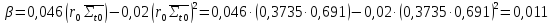
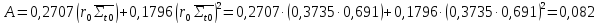
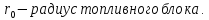
Площадь
миграции нейтронов –
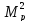 :
:
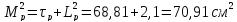
Геометрический
параметр реактора –
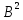 :
:
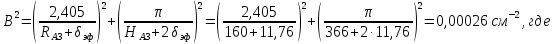
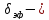 эффективная
добавка
эффективная
добавка
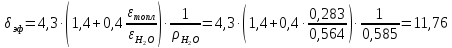
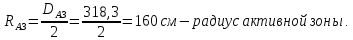
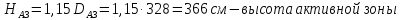
Эффективный
коэффициент размножения –
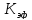 :
:
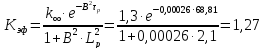
Итоговая таблица расчетов.
|
Параметр |
Шаг решетки Вр=12,75, мм |
|
|
Горячий реактор |
Холодный реактор |
|
|
DАЗ, мм |
3280 |
3280 |
|
nтвэл |
312 |
312 |
|
nк |
170 |
170 |
|
Sк, мм |
235,95 |
235,95 |
|
Vмк, мм3 |
253536,5 |
253536,5 |
|
Vкпр, мм3 |
25665,27 |
25665,27 |
|
VАЗпр, мм3 |
4616632,4 |
4616632,4 |
|
VH2OАЗ, мм3 |
4640248,3 |
4640248,3 |
|
VтоплАЗ, мм3 |
2346156,93 |
2346156,93 |
|
w |
1,97 |
1,97 |
|
Vяч, мм3 |
158,41 |
158,41 |
|
V0, мм3 |
45,36 |
45,36 |
|
V1, мм3 |
76,204 |
76,204 |
|
V2, мм3 |
36,846 |
36,846 |
|
d0, мм |
7,59 |
7,59 |
|
d1, мм |
14,2 |
14,2 |
|
d2, мм |
10,23 |
10,23 |
|
εтопл |
0,286 |
0,286 |
|
εH2O |
0,481 |
0,481 |
|
εоб |
0,232 |
0,232 |
|
δt |
0,01809 |
0,025417 |
|
C |
0,1221 |
0,16923 |
|
γp |
0,08487 |
0,11956 |
|
Q00 |
0,2335 |
0,177839 |
|
δ28 |
0,07494 |
0,05706 |
|
μ |
1,0341 |
1,0268 |
|
φ5 |
0,780149 |
0,844046 |
|
φZr |
0,979207 |
0,9857529 |
|
φNb |
0,9983679 |
0,998885 |
|
φSn |
0,99846487 |
0,998951 |
|
φFe |
0,999820665 |
0,99987752 |
|
|
22,48356 |
23,832 |
|
φ8 |
0,749002 |
0,811225 |
|
φ |
0,57027 |
0,6734139 |
|
|
0,2395877 |
0,2430257 |
|
|
0,4599657 |
0,67346379 |
|
Tn, K |
942,77904 |
830,7137 |
|
k,
|
0,49455 |
0,52868 |
|
|
0,91198 |
0,9203 |
|
|
0,96787 |
0,96879 |
|
|
0,32542285 |
0,34957262 |
|
|
0,0337672339 |
0,039739075 |
|
|
0,004178562 |
0,004451556 |
|
|
0,270360632 |
0,288297643 |
|
R |
0,18492846 |
0,201517 |
|
Q0 |
1,039725468 |
1,04288947 |
|
X0 |
0,00111946 |
0,001315168 |
|
|
0,0062289 |
0,006698 |
|
|
0,0005048 |
0,001089 |
|
ζ |
1,185748 |
1,1895 |
|
δ |
0,012463 |
0,014773 |
|
|
0,032564 |
0,070259 |
|
|
0,00319327 |
0,0034055 |
|
|
30,70858 |
14,23303 |
|
|
2,30818 |
2,15495 |
|
D |
0,0129679 |
0,016088 |
|
B |
1,053703 |
1,057046 |
|
q |
0,207058 |
0,22848 |
|
θ |
0,82846 |
0,814014 |
|
|
1,9199 |
1,89211 |
|
|
1,58568 |
1,58568 |
|
|
0,937979 |
1,06499 |
|
|
0,27 |
0,2059 |
|
|
1,2079 |
1,2709 |
|
|
7,17998 |
4,40147 |
|
|
63,547 |
41,699 |
|
δэф |
10,3447 |
7,0427 |
|
|
0,00025263 |
0,000262 |
|
|
70,727 |
46,10047 |
|
Kэф |
1,1865 |
1,25564 |
|
|
0,002939 |
0,005876 |
|
ρ |
0,157185 |
0,2036 |
|
|
-0,0464 |
|
|
|
-0,000683 |
|
|
θотр |
0,79577 |
0,78235 |
|
|
1,17096 |
1,229465 |
|
|
1,1499 |
1,21458 |
|
|
8,1084 |
4,40147 |
|
|
0,13036 |
0,1766 |
|
KB |
0,72176 |
0,56212 |

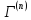
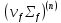
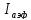 ∙10-24,
см2
∙10-24,
см2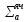 ,
см-1
,
см-1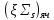 ,
см-1
,
см-1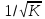
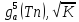
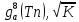
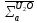 ,
см-1
,
см-1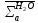 ,
см-1
,
см-1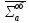 ,
см-1
,
см-1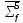 ,
см-1
,
см-1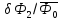
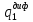
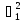 ,
см-2
,
см-2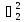 ,
см-2
,
см-2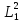 ,
см2
,
см2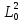 ,
см2
,
см2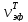
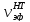
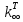
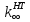
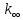
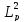 ,
см2
,
см2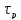 ,см2
,см2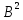 ,
см-2
,
см-2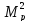 ,
см2
,
см2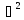 ,
см-2
,
см-2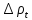
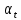
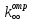
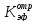
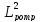 ,
см2
,
см2