
- •1.1.2. Условия лежандра
- •1.1.5. Функционалы со многими неизвестными
- •1.1.9. Задачи нл условный экстремум
- •1.1.10. О решении задач оптимального управления вариационными методами
- •1.2. Метод динамического программирования
- •1.2.1. Принцип оптимальности
- •1.2.2. Одномерная дискретная задача и вычислительные аспекты метода
- •1.2.3. Метод динамического программирования в непрерывной задаче. Уравнение беллмана
- •1.3. Принцип максимума понтрягина
- •1.3.1. Игольчатая вариация и условия оптимальности
- •1.3.2. Система сопряженных уравнений
- •1.3.3. Обобщения. Обсуждение результатов
- •Неавтономный объект с закрепленными концами траектории и фиксированным временем управления
- •Неавтономный объект с закрепленными концами траектории и нефиксированным временем управления
- •Неавтономный объект со свободным правым концом траектории и нефиксированным временем управления
- •Оптимальное управление автономными объектами
- •1.3.4. Вычислительные аспекты принципа максимума
Неавтономный объект с закрепленными концами траектории и нефиксированным временем управления
Чтобы
управление
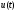 было оптимальным для
было оптимальным для
 ,
необходимо существование такой ненулевой
непрерывной вектор-функции
,
необходимо существование такой ненулевой
непрерывной вектор-функции
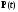 ,
соответствующей функциям
,
соответствующей функциям
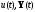 ,
и сопряженной системе (1.89), чтобы при
любом
,
и сопряженной системе (1.89), чтобы при
любом
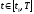 :
1) функция
:
1) функция
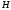 ,
определяемая соотношением (1.85), достигала
максимума по
,
определяемая соотношением (1.85), достигала
максимума по
 ;
2) выполнялось условие
;
2) выполнялось условие
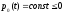 ,
а также в конечный момент времени было
справедливо
,
а также в конечный момент времени было
справедливо
 .
.
Последнее
условие, утверждающее, что максимальное
значение гамильтониана, соответствующее
оптимальным управлению и функциям
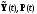 ,
в конечный момент времени должно
равняться нулю, является своеобразным
условием для отыскания неизвестного
момента
,
в конечный момент времени должно
равняться нулю, является своеобразным
условием для отыскания неизвестного
момента
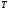 .
Текущее максимальное значение
гамильтониана на оптимальной траектории
изменяется по закону
.
Текущее максимальное значение
гамильтониана на оптимальной траектории
изменяется по закону
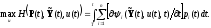
Неавтономный объект со свободным правым концом траектории и нефиксированным временем управления
Чтобы
управление
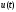 было оптимальным для
было оптимальным для
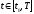 ,
необходимо существование такой ненулевой
непрерывной вектор-функции
,
необходимо существование такой ненулевой
непрерывной вектор-функции
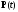 ,
соответствующей функциям
,
соответствующей функциям
 и сопряженной системе (1.89), чтобы 1) при
любом
и сопряженной системе (1.89), чтобы 1) при
любом
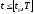 функция
функция
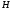 ,
определяемая соотношением (1.85), достигала
максимума по
,
определяемая соотношением (1.85), достигала
максимума по
 2) в конечный момент времени выполнялись
условия
2) в конечный момент времени выполнялись
условия
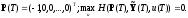
Последнее
условие служит для отыскания неизвестного
момента
 .
.
Оптимальное управление автономными объектами
Уравнения
объекта и критерии качества не содержат
в явном виде аргумент
 .
Формулировка необходимых условий
оптимальности полностью совпадает с
рассмотренными случаями управления
неавтономными объектами. Отличие
проявляется только в поведении
максимального значения гамильтониана
на оптимальной траектории при
нефиксированном времени управления. В
задачах управления автономными объектами
наибольшее значение гамильтониана в
любой момент времени постоянно и равно
нулю. Необходимость введения переменных
.
Формулировка необходимых условий
оптимальности полностью совпадает с
рассмотренными случаями управления
неавтономными объектами. Отличие
проявляется только в поведении
максимального значения гамильтониана
на оптимальной траектории при
нефиксированном времени управления. В
задачах управления автономными объектами
наибольшее значение гамильтониана в
любой момент времени постоянно и равно
нулю. Необходимость введения переменных
 в этих задачах отпадает, что приводит
к понижению порядков уравнений (1.75) и
(1.90).
в этих задачах отпадает, что приводит
к понижению порядков уравнений (1.75) и
(1.90).
Принцип максимума с использованием условий трансверсальности обобщается на случаи подвижных концов траектории. Результаты соответствующих обобщений систематизированы, например, в [3, 26, 48].
Остановимся
на отличиях формулировок принципа
максимума в зависимости от особенностей
задачи оптимального управления. Основное
содержание принципа максимума сводится
к условию (1.86), утверждающему, что
оптимальное управление в любой момент
времени должно доставлять наибольшее
значение гамильтониану
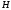 .
Из этого условия принципиально можно
найти оптимальное управление
.
Из этого условия принципиально можно
найти оптимальное управление
 как функцию пока неизвестных переменных
как функцию пока неизвестных переменных
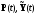 .
Если оптимальное управление подставить
в (1.75), (1.89) или (1.90), то певучим систему
из
.
Если оптимальное управление подставить
в (1.75), (1.89) или (1.90), то певучим систему
из
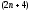 уравнений с таким же количеством
неизвестных
уравнений с таким же количеством
неизвестных
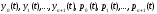 .
Для решения системы формально нужно
иметь
.
Для решения системы формально нужно
иметь
 условий. Имеем
условий. Имеем
 условий в начальной точке
условий в начальной точке
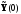 ,
а остальные
,
а остальные
 условий формируются различным образом
в зависимости от конкретных особенностей
задачи:
условий формируются различным образом
в зависимости от конкретных особенностей
задачи:
а) если
правый конец траектории свободен, то
получаем
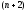 условий в виде величины
условий в виде величины
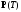 ;
если при этом
;
если при этом
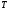 фиксировано, то всегда будем иметь
фиксировано, то всегда будем иметь
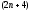 условий, необходимых для решения задачи;
если же
условий, необходимых для решения задачи;
если же
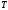 неизвестно, то используем дополнительное
ограничение на максимальное значение
гамильтониана, что снова устанавливает
соответствие между количеством
неизвестных и граничных условий;
неизвестно, то используем дополнительное
ограничение на максимальное значение
гамильтониана, что снова устанавливает
соответствие между количеством
неизвестных и граничных условий;
б) если
правый конец траектории закреплен, то
вместо
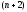 значений
значений
 используем
используем
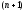 заданных условий в виде
заданных условий в виде
 .
Так как функция Гамильтона (1.85) зависит
от вектора
.
Так как функция Гамильтона (1.85) зависит
от вектора
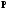 линейно, то этот вектор может быть
определен с точностью до постоянного
сомножителя, который не повлияет на
оптимальное управление
линейно, то этот вектор может быть
определен с точностью до постоянного
сомножителя, который не повлияет на
оптимальное управление
 .
Поэтому в соответствии с ограничением
можно принять
.
Поэтому в соответствии с ограничением
можно принять
 ,
что дает еще одно условие и делает равным
число неизвестных и имеющихся условий,
используемых при отыскании постоянных
интегрирования. Если же
,
что дает еще одно условие и делает равным
число неизвестных и имеющихся условий,
используемых при отыскании постоянных
интегрирования. Если же
 неизвестно, то дополнительно учитываем
ограничение на максимальное значение
гамильтониана в конечной точке.
неизвестно, то дополнительно учитываем
ограничение на максимальное значение
гамильтониана в конечной точке.
Таким образом, при использовании принципа максимума приходим к краевой задаче для систем дифференциальных уравнений. Универсального рецепта решения этой задачи в настоящее время нет. В каждой задаче проводится самостоятельное исследование. Полезно отметить, что существует связь принципа максимума с вариационными методами и методом динамического программирования, позволяющая при определенных условиях установить существо каждого из этих методов на основании другого метода.
Рассмотрим применимость принципа максимума на ряде задач, допускающих аналитическое решение.
Пример
1.12. С использованием принципа максимума
решим задачу 1.9, ранее исследованную в
терминах вариационного исчисления. В
соответствии с основными принципами
формализма метода вводим вектор
 ,
задаваемый уравнениями
,
задаваемый уравнениями
 .
Переменная (1.70) не используется, так как
время
.
Переменная (1.70) не используется, так как
время
 в явном виде не участвует в формировании
уравнений объекта и критерия качества.
Далее, на основании (1.85) составляем
гамильтониан
в явном виде не участвует в формировании
уравнений объекта и критерия качества.
Далее, на основании (1.85) составляем
гамильтониан
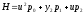 и в соответствии с принципом максимума
оптимальное управление ищем из условия
его максимума. Так как на
и в соответствии с принципом максимума
оптимальное управление ищем из условия
его максимума. Так как на
 ограничений
нет, то соответствующее условие принимает
вид
ограничений
нет, то соответствующее условие принимает
вид
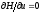 и приводит к результату
и приводит к результату
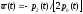 .
На основании (1.90) составляем систему
сопряженных уравнений:
.
На основании (1.90) составляем систему
сопряженных уравнений:
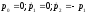 из которой следует
из которой следует
 .
Так как решается задача с фиксированным
временем управления и закрепленными
концами траектории, принимаем
.
Так как решается задача с фиксированным
временем управления и закрепленными
концами траектории, принимаем
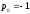 .
Коэффициенты
.
Коэффициенты
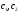 должны обеспечить прохождение траектории
через заданные граничные точки. С этой
целью оптимальное управление
должны обеспечить прохождение траектории
через заданные граничные точки. С этой
целью оптимальное управление
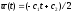 подставляем в уравнения объекта, которые
после интегрирования дают
подставляем в уравнения объекта, которые
после интегрирования дают
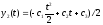 ;
;
 ,теперь
постоянные
,теперь
постоянные
 легко найти из четырех заданных
граничных условий. Решение задачи, таким
образом, полностью совпадает с результатами
примера 1.9.
легко найти из четырех заданных
граничных условий. Решение задачи, таким
образом, полностью совпадает с результатами
примера 1.9.
Пример
1.13. Рассмотрим
одномерный объект с уравнением
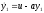 при заданном начальном состоянии
при заданном начальном состоянии
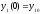 и при
отсутствии ограничений на
и при
отсутствии ограничений на
 .
Критерий качества
.
Критерий качества
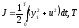 фиксировано, подлежит минимизации.
В данном
случае имеем задачу со свободным правым
концом траектории. Модифицированное
состояние описывается уравнениями
фиксировано, подлежит минимизации.
В данном
случае имеем задачу со свободным правым
концом траектории. Модифицированное
состояние описывается уравнениями
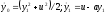 .
Из общего определения (1.85) следует
гамильтониан
.
Из общего определения (1.85) следует
гамильтониан
 .
Максимизирующее гамильтониан оптимальное
управление оказывается равным
.
Максимизирующее гамильтониан оптимальное
управление оказывается равным
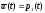 .
Система сопряженных уравнений (1.90)
принимает вид
.
Система сопряженных уравнений (1.90)
принимает вид
 .
Так как правый
конец траектории свободный, выполняется
условие
.
Так как правый
конец траектории свободный, выполняется
условие
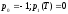 .
Для нахождения
.
Для нахождения
 следует
совместно решить сопряженное уравнение
и уравнение объекта, т. е. систему
следует
совместно решить сопряженное уравнение
и уравнение объекта, т. е. систему
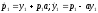 ,
при условиях
,
при условиях
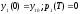 .
Разрешив первое
уравнение относительно
.
Разрешив первое
уравнение относительно
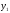 и подставив его во второе, приходим к
однородному уравнению
и подставив его во второе, приходим к
однородному уравнению
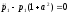 ,
которое имеет
решение
,
которое имеет
решение
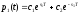 ,
где —
,
где —
 — корень
характеристического уравнения
— корень
характеристического уравнения
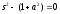 .
Для определения постоянных интегрирования
.
Для определения постоянных интегрирования
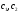 используем граничное условие
используем граничное условие
 и при
и при
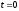 — сопряженное уравнение
— сопряженное уравнение
 .
.
В
результате получаем систему уравнений
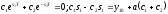 ,
из которой находим
,
из которой находим
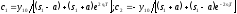 .
Оптимальное
управление принимает окончательный
вид
.
Оптимальное
управление принимает окончательный
вид
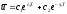 .
.
Пример
1.14. Рассмотрим
особенности применения принципа
максимума в задаче с ограничением на
управление. Пусть ОУ описывается
уравнением
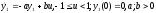 .
Требуется найти управление, при котором
величина
.
Требуется найти управление, при котором
величина
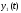 в известный
момент
в известный
момент
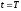 окажется
наибольшей. Очевидно, что таким управлением
должно быть
окажется
наибольшей. Очевидно, что таким управлением
должно быть
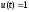 .
Докажем это предположение с помощью
принципа максимума. Прежде всего,
введем минимизируемый критерий качества
.
Докажем это предположение с помощью
принципа максимума. Прежде всего,
введем минимизируемый критерий качества
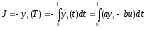 и составим
систему уравнений
и составим
систему уравнений
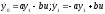 ,
в соответствии с которой формируем
,
в соответствии с которой формируем
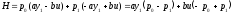 .
Находим управление, максимизирующее
.
Находим управление, максимизирующее
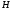 .
Так как
.
Так как
 в
в
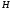 входит линейно, то
входит линейно, то
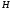 при ограничении
при ограничении
 достигает наибольшего значения, если
достигает наибольшего значения, если
 максимально по модулю, а знак таков, что
второе слагаемое в составе
максимально по модулю, а знак таков, что
второе слагаемое в составе
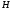 максимально. Это условие обеспечивается,
если
максимально. Это условие обеспечивается,
если
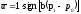 ,
где
,
где
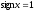 при
при
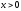 и
и
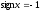 при
при
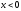 .
В соответствии с (1.90) составляем систему
сопряженных уравнений
.
В соответствии с (1.90) составляем систему
сопряженных уравнений
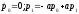 .
Из первого уравнения следует
.
Из первого уравнения следует
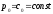 .
.
Задавшись
произвольным начальным условием
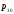 решаем второе
уравнение:
решаем второе
уравнение:
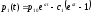 .
Так как рассматриваемая задача
характеризуется свободным правым концом
и фиксированным
.
Так как рассматриваемая задача
характеризуется свободным правым концом
и фиксированным
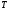 ,
то выполняется граничное условие
,
то выполняется граничное условие
 .
Следовательно,
.
Следовательно,
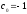 ,
а начальная величина
,
а начальная величина
 находится из условия
находится из условия
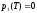 .
Поэтому
.
Поэтому
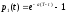 ,
и оптимальное управление принимает
окончательный, вид
,
и оптимальное управление принимает
окончательный, вид
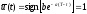 ,
что совпадает с нашим начальным
предположением.
,
что совпадает с нашим начальным
предположением.
Если
предположить, что величина
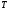 не задана, необходимо использовать
дополнительное условие
не задана, необходимо использовать
дополнительное условие
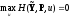 ,
в соответствии
с которым
вычисляют гамильтониан на оптимальной
траектории в какой-либо момент времени.
Проще всего это сделать для
,
в соответствии
с которым
вычисляют гамильтониан на оптимальной
траектории в какой-либо момент времени.
Проще всего это сделать для
 .
Имеем
.
Имеем
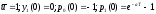 .
Подставив эти значения в
.
Подставив эти значения в
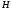 ,
находим
,
находим
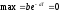 ,
откуда
,
откуда
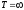 .
Следовательно, если
.
Следовательно, если
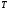 не задано, величина
не задано, величина
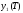 достигает
наибольшего значения при
достигает
наибольшего значения при
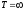 .
Этот результат очевиден: если на
рассматриваемый объект подать единичное
управление, то выходной процесс начинает
возрастать по экспоненциальному закону.
Максимальное значение достигается на
бесконечности.
.
Этот результат очевиден: если на
рассматриваемый объект подать единичное
управление, то выходной процесс начинает
возрастать по экспоненциальному закону.
Максимальное значение достигается на
бесконечности.
