
- •1.1.2. Условия лежандра
- •1.1.5. Функционалы со многими неизвестными
- •1.1.9. Задачи нл условный экстремум
- •1.1.10. О решении задач оптимального управления вариационными методами
- •1.2. Метод динамического программирования
- •1.2.1. Принцип оптимальности
- •1.2.2. Одномерная дискретная задача и вычислительные аспекты метода
- •1.2.3. Метод динамического программирования в непрерывной задаче. Уравнение беллмана
- •1.3. Принцип максимума понтрягина
- •1.3.1. Игольчатая вариация и условия оптимальности
- •1.3.2. Система сопряженных уравнений
- •1.3.3. Обобщения. Обсуждение результатов
- •Неавтономный объект с закрепленными концами траектории и фиксированным временем управления
- •Неавтономный объект с закрепленными концами траектории и нефиксированным временем управления
- •Неавтономный объект со свободным правым концом траектории и нефиксированным временем управления
- •Оптимальное управление автономными объектами
- •1.3.4. Вычислительные аспекты принципа максимума
1.1.10. О решении задач оптимального управления вариационными методами
Сформулированная во введении задача оптимального управления существенно напоминает общую задачу Лагранжа классического вариационного исчисления. Действительно, при оптимальном управлении мы имеем объект управления, описываемый системой дифференциальных уравнений
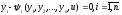 (1.38)
(1.38)
Заданы
начальное и конечное состояния объекта
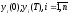 ,
и критерий оптимальности
,
и критерий оптимальности
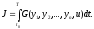 (1.39)
(1.39)
В области
допустимых управлений
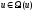 необходимо найти такое управление
необходимо найти такое управление
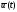 ,
на котором критерий оптимальности
достигнет наименьшего значения, а объект
переводится из заданного начального
состояния в заданное конечное по
траектории, принадлежащей области
допустимых значений.
,
на котором критерий оптимальности
достигнет наименьшего значения, а объект
переводится из заданного начального
состояния в заданное конечное по
траектории, принадлежащей области
допустимых значений.
Уравнения
объекта можно рассматривать как аналоги
дифференциальных уравнений связей в
вариационном исчислении. Критерий
оптимальности представляет по существу
минимизируемый функционал. Совокупность
функций
 расценивается как система неизвестных
и подлежащих определению функций. Если
предположить, что на управления и
состояния никаких ограничений не
наложено, и они могут быть гладкими
функциями, то решение задачи можно
искать в соответствии с используемой
в вариационном исчислении схемой.
расценивается как система неизвестных
и подлежащих определению функций. Если
предположить, что на управления и
состояния никаких ограничений не
наложено, и они могут быть гладкими
функциями, то решение задачи можно
искать в соответствии с используемой
в вариационном исчислении схемой.
С этой целью составляется вспомогательный функционал
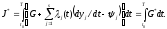 (1.40)
(1.40)
Здесь
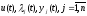 — независимые переменные.
— независимые переменные.
Относительно
функций
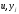 составляют уравнения Эйлера, к ним
добавляют уравнения объекта управления
и получают систему из
составляют уравнения Эйлера, к ним
добавляют уравнения объекта управления
и получают систему из
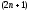 уравнений
уравнений
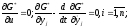

с таким же числом неизвестных
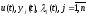 .
Заметим, что замыкающие систему уравнения
объекта можно трактовать как уравнения
Эйлера относительно неопределенных
множителей Лагранжа:
.
Заметим, что замыкающие систему уравнения
объекта можно трактовать как уравнения
Эйлера относительно неопределенных
множителей Лагранжа:
 .
Последнюю систему можно переписать
в виде
.
Последнюю систему можно переписать
в виде
 (1.41)
(1.41)
 (1.42)
(1.42)
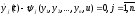 (1.43)
(1.43)
Уравнение
(1.41) является алгебраическим. Оставшиеся
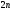 уравнений представляют систему
дифференциальных уравнений первого
порядка. При их решении необходимо
определить
уравнений представляют систему
дифференциальных уравнений первого
порядка. При их решении необходимо
определить
 постоянных интегрирования, которые
вычисляются на основании такого же
количества заданных граничных условий.
Этот процесс вычисления, связанный с
решением двухточечной краевой задачи
(траектория должна пройти через заданные
начальную и конечную точки), может
оказаться весьма трудоемким. Однако
принципиально система (1.41) — (1.43),
состоящая из
постоянных интегрирования, которые
вычисляются на основании такого же
количества заданных граничных условий.
Этот процесс вычисления, связанный с
решением двухточечной краевой задачи
(траектория должна пройти через заданные
начальную и конечную точки), может
оказаться весьма трудоемким. Однако
принципиально система (1.41) — (1.43),
состоящая из
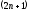 уравнений и содержащая такое же количество
неизвестных, позволяет отыскать все
неизвестные, включая оптимальное
управление
уравнений и содержащая такое же количество
неизвестных, позволяет отыскать все
неизвестные, включая оптимальное
управление
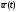 .
.
Пример
1.9. Пусть
имеется одномерный ОУ, описываемый
уравнением
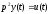 ,
и заданы
граничные условия
,
и заданы
граничные условия
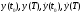 .
.
Качество
системы описывается функционалом
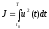 .
Необходимо отыскать управление
.
Необходимо отыскать управление
 ,
минимизирующее
,
минимизирующее
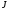 и переводящее
объект из начального состояния в
конечное. Это и есть задача о минимальных
энергетических затратах, уже обсуждавшаяся
во введении. Для решения задачи представим
уравнение ОУ в форме Коши, положив
и переводящее
объект из начального состояния в
конечное. Это и есть задача о минимальных
энергетических затратах, уже обсуждавшаяся
во введении. Для решения задачи представим
уравнение ОУ в форме Коши, положив
 ,
тогда
,
тогда
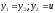 и
и
 .
Составим
вспомогательный функционал
.
Составим
вспомогательный функционал

и по
переменным
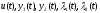 запишем систему уравнений Эйлера
запишем систему уравнений Эйлера
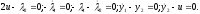
Из
второго уравнения следует
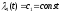 ,
из третьего
,
из третьего
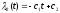 ,
из первого
,
из первого
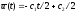 из пятого
из пятого
 и, наконец, из
четвертого
и, наконец, из
четвертого
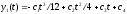 .
Для
вычисления постоянных интегрирования
составим систему уравнений в соответствии
с граничными условиями (при
.
Для
вычисления постоянных интегрирования
составим систему уравнений в соответствии
с граничными условиями (при
 ):
):
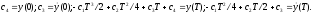
Отсюда
легко находим постоянные
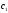 и
и
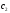 и этим завершаем
поиск оптимального управления
и этим завершаем
поиск оптимального управления
 .
.
Задачу можно решать и без перехода к уравнениям в форме Коши, составив вспомогательный функционал с учетом исходного уравнения ОУ. В этом случае
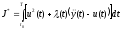
и минимизация
осуществляется по трем переменным
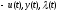 .
Однако по
переменной
.
Однако по
переменной
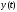 нужно
пользоваться не уравнением Эйлера, а
уравнением Эйлера — Пуассона (1.17).
Соответствующая система уравнений
принимает вид
нужно
пользоваться не уравнением Эйлера, а
уравнением Эйлера — Пуассона (1.17).
Соответствующая система уравнений
принимает вид

Из
второго уравнения следует
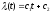 ,
из первого
,
из первого
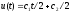 ,
из третьего
,
из третьего
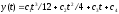 .
Постоянные
интегрирования по-прежнему находим из
граничных условий, и решение
тождественно совпадает с предыдущим.
.
Постоянные
интегрирования по-прежнему находим из
граничных условий, и решение
тождественно совпадает с предыдущим.
Поиск
оптимального управления средствами
вариационного исчисления значительно
усложняется, если учитывать ограничения
на области допустимых управлений и
состояний, имеющихся в любой технической
задаче. Наличие ограничений приводит
к тому, что в пространстве управлений
оптимальные управлении не могут
выходить за пределы некоторой допустимой
области, но могут оказаться на ее границе,
и тогда управление нельзя найти из
обычного уравнения Эйлера. Это обусловлено
тем, что при выводе уравнения Эйлера мы
придавали функции
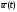 вариацию
вариацию
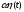 ,
где
,
где
 — малая величина, произвольная по знаку.
Поэтому вариацию
— малая величина, произвольная по знаку.
Поэтому вариацию
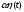 называют двусторонней. Если
управление находится на границе
допустимой области, то двустороннюю
вариацию применять нельзя, так как при
определенном знаке
называют двусторонней. Если
управление находится на границе
допустимой области, то двустороннюю
вариацию применять нельзя, так как при
определенном знаке
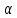 функция
функция
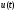 выйдет из допустимой области. Вариация
должна быть односторонней, но тогда
мы не придем к уравнению Эйлера. Возникшую
трудность в вариационном исчислении
преодолевают переходом к новой переменной,
построенной таким образом, что ограничения
на
выйдет из допустимой области. Вариация
должна быть односторонней, но тогда
мы не придем к уравнению Эйлера. Возникшую
трудность в вариационном исчислении
преодолевают переходом к новой переменной,
построенной таким образом, что ограничения
на
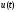 не приводят к ограничениям на эту
новую переменную. Относительно новой
переменной можно пользоваться обычным
уравнением Эйлера, найти экстремали и
точки, в которых экстремали сочленяются
с границей допустимой области. В
результате функция
не приводят к ограничениям на эту
новую переменную. Относительно новой
переменной можно пользоваться обычным
уравнением Эйлера, найти экстремали и
точки, в которых экстремали сочленяются
с границей допустимой области. В
результате функция
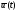 будет состоять из экстремалей
(лежащих в допустимой области решений
уравнений Эйлера) и отдельных участков
границы допустимой области.
будет состоять из экстремалей
(лежащих в допустимой области решений
уравнений Эйлера) и отдельных участков
границы допустимой области.
Изложенный
подход вариационного исчисления к
решению задач с ограничениями применяется
тогда, когда минимизируемый функционал
зависит от производных функции
 и не является вырожденным. В задачах
оптимального управления критерии
оптимальности, как правило, этих
производных не содержат, и использование
уравнения Эйлера может привести к
утверждению, что экстремалей нет вообще.
Последнее может означать, что оптимальная
функция
и не является вырожденным. В задачах
оптимального управления критерии
оптимальности, как правило, этих
производных не содержат, и использование
уравнения Эйлера может привести к
утверждению, что экстремалей нет вообще.
Последнее может означать, что оптимальная
функция
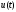 находится только на границах допустимой
области. Однако поведение этой функции
на границах (например, точки перехода
с одной границы на другую, число этих
переходов и т. п.) установить вариационными
методами в практически приемлемой форме
не удается.
находится только на границах допустимой
области. Однако поведение этой функции
на границах (например, точки перехода
с одной границы на другую, число этих
переходов и т. п.) установить вариационными
методами в практически приемлемой форме
не удается.
Пример
1.10. Состояние
объекта управления описывается
уравнениями
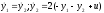 при граничных
условиях
при граничных
условиях
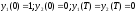 .
На управление
задано ограничение
.
На управление
задано ограничение
 .
.
Необходимо
минимизировать критерий качества
 и перевести ОУ из начального в конечное
состояние.
и перевести ОУ из начального в конечное
состояние.
Введем
новую переменную,
 связанную с
связанную с
 соотношением
соотношением
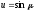 .
Переменная
.
Переменная
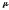 может принимать любые значения, и при
этом всегда будет выполнено исходное
ограничение
может принимать любые значения, и при
этом всегда будет выполнено исходное
ограничение
 .
Следовательно, на
.
Следовательно, на
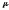 ограничения
не налагаются. Относительно переменной
ограничения
не налагаются. Относительно переменной
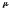 теперь можем решать задачу на условный
экстремум, используя метод множителей
Лагранжа. Составляем функцию
теперь можем решать задачу на условный
экстремум, используя метод множителей
Лагранжа. Составляем функцию
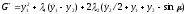
и по переменным
 записываем уравнения Эйлера:
записываем уравнения Эйлера:
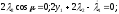

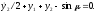
Первое
уравнение выполняется, если
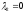 или
или
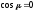 .
Но если на некотором отрезке
.
Но если на некотором отрезке
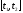 из
из
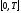 имеем
имеем
 ,
то из третьего уравнения следует
,
то из третьего уравнения следует
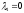 и из остальных
уравнений получаем
и из остальных
уравнений получаем
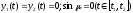 ,
т.е. оптимальное
управление оказывается нулевым на
отрезке
,
т.е. оптимальное
управление оказывается нулевым на
отрезке
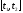 .
Так как при этом выполняются условия
.
Так как при этом выполняются условия
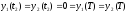 ,
то управление
следует положить равным нулю и па отрезке
,
то управление
следует положить равным нулю и па отрезке
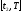 ,
иначе величина
функционала
,
иначе величина
функционала
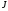 лишь возрастет. На полуинтервале
лишь возрастет. На полуинтервале
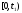 имеем
имеем
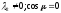 .
Но это значит, что
.
Но это значит, что
 и
и
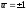 ,
т. е. оптимальное управление находится
на границе области допустимых управлений
и может переходить с одной границы
на другую. Если управление искать только
в классе непрерывных функций, то следует
принять, что
,
т. е. оптимальное управление находится
на границе области допустимых управлений
и может переходить с одной границы
на другую. Если управление искать только
в классе непрерывных функций, то следует
принять, что
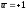 или
или
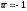 .
Однако нетрудно убедиться, что ни одно
из этих управлений не позволит
удовлетворять конечные условия
.
Однако нетрудно убедиться, что ни одно
из этих управлений не позволит
удовлетворять конечные условия
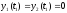 при начальных
при начальных
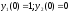 .
Поэтому оптимальное управление может
быть только разрывным и переходить в
точках разрыва с одной границы на другую.
Однако число переходов и моменты перехода
установить не удается.
.
Поэтому оптимальное управление может
быть только разрывным и переходить в
точках разрыва с одной границы на другую.
Однако число переходов и моменты перехода
установить не удается.
Таким образом, можем сделать ряд выводов о применимости методов классического вариационного исчисления к решению задач оптимального управления. Задачи оптимального управления обладают рядом особенностей по сравнению с задачами вариационного исчисления.
1. Искомые управления принадлежат замкнутым областям допустимых управлений, поэтому могут совпадать с границами этих областей. Однако дать количественную оценку поведения управления на границе допустимой области вариационными средствами очень трудно. Это же относится и к переменным состояния.
2.
Критерий оптимальности не зависит от
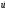 ,
поэтому уравнения Эйлера по управлению
не являются дифференциальными.
,
поэтому уравнения Эйлера по управлению
не являются дифференциальными.
3. В задаче оптимального управления оптимальные управления ищутся в классе кусочно-непрерывных функций. Часто критерии оптимальности достигают минимума на управлениях, имеющих разрывы первого рода. Число и положение точек разрыва заранее неизвестны.
Все эти
особенности задач оптимального управления
приводят к тому, что применение ко многим
из них методов классического вариационного
исчисления, ориентированных на гладкие
дифференцируемые функции, даже после
надлежащей модернизации остается
проблематичным. Поэтому для решения
задач оптимального управления разработаны
специальные методы, наиболее полно и
рационально учитывающие специфику этих
задач. Если же задача оптимального
управления сформулирована так, что
функция
 в составе критерия качества является
дважды дифференцируемой, а управления
и переменные состояния не достигают
ограничений, задачу можно решать
вариационными методами.
в составе критерия качества является
дважды дифференцируемой, а управления
и переменные состояния не достигают
ограничений, задачу можно решать
вариационными методами.
