
- •1.1.2. Условия лежандра
- •1.1.5. Функционалы со многими неизвестными
- •1.1.9. Задачи нл условный экстремум
- •1.1.10. О решении задач оптимального управления вариационными методами
- •1.2. Метод динамического программирования
- •1.2.1. Принцип оптимальности
- •1.2.2. Одномерная дискретная задача и вычислительные аспекты метода
- •1.2.3. Метод динамического программирования в непрерывной задаче. Уравнение беллмана
- •1.3. Принцип максимума понтрягина
- •1.3.1. Игольчатая вариация и условия оптимальности
- •1.3.2. Система сопряженных уравнений
- •1.3.3. Обобщения. Обсуждение результатов
- •Неавтономный объект с закрепленными концами траектории и фиксированным временем управления
- •Неавтономный объект с закрепленными концами траектории и нефиксированным временем управления
- •Неавтономный объект со свободным правым концом траектории и нефиксированным временем управления
- •Оптимальное управление автономными объектами
- •1.3.4. Вычислительные аспекты принципа максимума
1.3.2. Система сопряженных уравнений
Чтобы
воспользоваться принципом максимума
(1.86), необходимо определить вектор
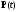 ;
он до сих пор не известен, хотя все
предыдущие выводы основывались на его
существовании. Продифференцировав
(1.83) по времени
;
он до сих пор не известен, хотя все
предыдущие выводы основывались на его
существовании. Продифференцировав
(1.83) по времени
 ,
запишем
,
запишем
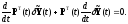 (1.87)
(1.87)
Компоненты
вектора
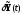 являются бесконечно малыми, так как
порождены игольчатой вариацией,
существующей на бесконечно малом
интервале времени. Найдем уравнение,
которое их описывает. За основу принимаем
уравнение объекта (1.75) и предполагаем,
что переменные
являются бесконечно малыми, так как
порождены игольчатой вариацией,
существующей на бесконечно малом
интервале времени. Найдем уравнение,
которое их описывает. За основу принимаем
уравнение объекта (1.75) и предполагаем,
что переменные
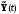 при всех
при всех
 изменились на бесконечно малые величины
изменились на бесконечно малые величины
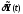 .
Допуская дифференцируемость функции
.
Допуская дифференцируемость функции
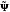 по аргументу
по аргументу
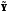 ,
из (1.75) в результате стандартной процедуры
линеаризации, основанной на разложении
нелинейных функций в ограниченный
линейными членами ряд Тейлора, получаем
уравнения в вариациях
,
из (1.75) в результате стандартной процедуры
линеаризации, основанной на разложении
нелинейных функций в ограниченный
линейными членами ряд Тейлора, получаем
уравнения в вариациях
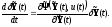 (1.88)
(1.88)
где производная от вектора по вектору понимается как матрица вида
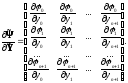
Учтем (1.88) в составе (1.87), тогда
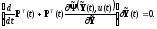
Произведение
сомножителей в левой части этого
соотношения должно равняться нулю при
любых функциях
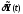 и
всех
и
всех
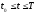 .
Это возможно, если первый сомножитель
равен нулю, т.е.
.
Это возможно, если первый сомножитель
равен нулю, т.е.
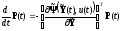 (1.89)
(1.89)
или в скалярной форме
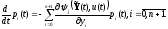 (1.90)
(1.90)
Уравнения
(1.89) или (1.90) образуют линейную систему,
позволяющую при граничных условиях
(1.81) совместно с уравнениями (1.75) и (1.86)
отыскать функции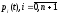
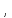 участвующие в формировании функции
Гамильтона. Система (1.89) или (1.90) называется
сопряженной по отношению к системе
уравнений объекта (1.75). Обе системы часто
объединяют общей формой записи, основанной
на введенной функции Гамильтона (1.85).
Из сопоставления соотношений (1.75),
(1.85) и (1.89) нетрудно установить
участвующие в формировании функции
Гамильтона. Система (1.89) или (1.90) называется
сопряженной по отношению к системе
уравнений объекта (1.75). Обе системы часто
объединяют общей формой записи, основанной
на введенной функции Гамильтона (1.85).
Из сопоставления соотношений (1.75),
(1.85) и (1.89) нетрудно установить
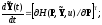
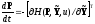
или в скалярной форме
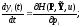
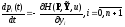
Эти соотношения называют каноническими уравнениями Гамильтона.
Оптимальное
управление ищут при совместном решении
уравнений (1.75), (1.86) и (1.90), содержащих
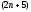 неизвестных
неизвестных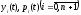 и
и
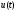 .
Соотношения (1.75) и (1.90) образуют систему
из
.
Соотношения (1.75) и (1.90) образуют систему
из
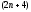 дифференциальных уравнений, решения
которых зависят от такого же числа
постоянных интегрирования. Для их
определения мы располагаем
дифференциальных уравнений, решения
которых зависят от такого же числа
постоянных интегрирования. Для их
определения мы располагаем
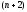 начальными условиями (1.76) и
начальными условиями (1.76) и
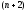 конечными условиями (1.81). Условие (1.86)
не приводит к дифференциальным уравнениям,
поэтому располагаем всеми данными,
достаточными для определения оптимального
управления из условия совместного
выполнения соотношений (1.75), (1.86) и (1.90).
конечными условиями (1.81). Условие (1.86)
не приводит к дифференциальным уравнениям,
поэтому располагаем всеми данными,
достаточными для определения оптимального
управления из условия совместного
выполнения соотношений (1.75), (1.86) и (1.90).
1.3.3. Обобщения. Обсуждение результатов
Принцип максимума обобщается на другие варианты задачи оптимального управления. Приведем некоторые из этих обобщений.
Неавтономный объект с закрепленными концами траектории и фиксированным временем управления
Чтобы
управление
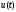 было оптимальным для
было оптимальным для
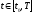 ,
необходимо существование такой ненулевой
непрерывной вектор функции
,
необходимо существование такой ненулевой
непрерывной вектор функции
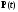 ,
соответствующей функциям
,
соответствующей функциям
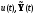 и сопряженной системе (1.89), чтобы при
любом
и сопряженной системе (1.89), чтобы при
любом
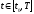 :
1) функция
:
1) функция
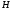 ,
определяемая соотношением (1.85), достигала
максимума по управлению
,
определяемая соотношением (1.85), достигала
максимума по управлению
 ;
2)
;
2)
 .
.
Система
(1.90) должна решаться при таких начальных
условиях
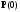 ,
при которых траектория объекта
,
при которых траектория объекта
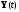 ,
найденная из решения системы (1.75) при
начальных условиях
,
найденная из решения системы (1.75) при
начальных условиях
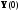 и соответствующем условию (1.86) оптимальном
управлении, пройдет через граничную
точку
и соответствующем условию (1.86) оптимальном
управлении, пройдет через граничную
точку
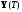 .
Эти начальные условия находят путем
последовательных приближений в
соответствии со специально разрабатываемыми
вычислительными схемами. Смысл
соответствующих операций сводится к
следующему. Для решения системы (1.75) и
(1.90), состоящей из
.
Эти начальные условия находят путем
последовательных приближений в
соответствии со специально разрабатываемыми
вычислительными схемами. Смысл
соответствующих операций сводится к
следующему. Для решения системы (1.75) и
(1.90), состоящей из
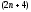 дифференциальных уравнений, необходимо
иметь
дифференциальных уравнений, необходимо
иметь
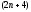 начальных
условий. Одна половина условий определена
заданным начальным состоянием объекта
начальных
условий. Одна половина условий определена
заданным начальным состоянием объекта
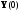 ,
другая половина зависит от начального
значения вектора
,
другая половина зависит от начального
значения вектора
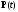 .
Если этим значением задаться произвольно
и решить совместно (1.75), (1.90) и (1.86), то
траектория
.
Если этим значением задаться произвольно
и решить совместно (1.75), (1.90) и (1.86), то
траектория
 не пройдет через точку
не пройдет через точку
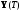 .
Начальные условия
.
Начальные условия
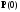 нужно изменить так, чтобы после повторения
всех вычислений траектория
нужно изменить так, чтобы после повторения
всех вычислений траектория
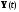 прошла через заданную граничную точку.
прошла через заданную граничную точку.
