1.3.4. Вычислительные аспекты принципа максимума

Рассмотренные примеры относятся к весьма узкому классу задач оптимизации, которые позволяют в аналитической форме получить решение. Подобные задачи являются скорее исключением, нежели правилом — большинство из них решается только численно на ЭВМ. Для повышения эффективности численных процедур поиска оптимальных решений разработаны определенные рекомендации, помогающие организовать рациональный процесс последовательного приближения к оптимальному решению. Рассмотрим одно из распространенных правил последовательного поиска оптимального управления (схема И. А. Крылова и Ф. JI. Черноусько). Для определенности будем ориентироваться на одномерную задачу с фиксированным временем управления и свободным правым концом траектории. Логика метода последовательных приближений основана на том, что выбирается некоторое допустимое управление и последовательно улучшается до тех пор, пока не окажет­ся подходящих допустимых вариаций управления, уменьшающих критерий качества. Существо метода изложим в форме следующей по­следовательности операций:

1. В области допустимых управлений 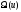задаются некоторым допустимым управлением 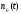— диспетчерским. Для простоты можно положить 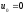если 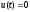— допустимое управление.

2. Управление 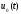подставляют в уравнение объекта управления (1.75) и интегрируют последнее при начальных условиях (1.76). Соответствующее решение обозначим .

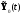3. На процессах 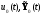вычисляют критерий качества .

4. Составляют систему сопряженных уравнений (1.90). Входящие в эти уравнения функции заменяют на 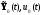, затем сопряженную систему интегрируют справа налево от 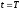до 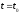при краевых условиях (1.81) (техника этой операции частично отражена в примере 1.11). Соответствующее решение обозначим символом .

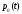5. В соответствии с (1.85) составляют выражение гамильтониана, в котором функции 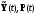заменяют на 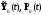результате получаем . Заметим, что управление 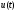не заменяется диспетчерским управлением .

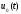6. Так как в составе гамильтониана неизвестным является только управление 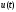, решается задача поиска такого допустимого управления, на котором функция 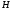достигает наибольшего значения. При использовании ЭВМ все процессы можно проквантовать по времени и для каждого дискретного момента вычислить максимизирующее управление в соответствии с каким-либо алгоритмом поиска экстремума функции. Соответствующие алгоритмы излагаются в гл. 6. Обозначим полученное в результате управление символом .

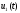7. Управление 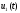принимается за первое приближение к оптимальному управлению, и относительно него проводятся операции 2, 3. Результат операции 2 обозначим символом .

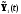8. Если окажется 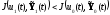, то проводятся операции 4—6, вследствие чего появляется второе приближение оптимального управления

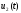
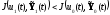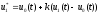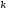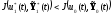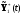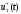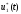9. Если окажется то первое приближение корректируется путем перехода к функции , где — эмпирически подбираемый коэффициент, обеспечивающий неравенство в составе которого является результатом операции 2 при управлении . Относительно проводятся последующие операции 4—6, вследствие чего появляется второе приближение .

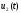10. С управлением 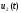проводятся все операции по схеме 2—9, что приводит к третьему приближению _.

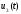11. Вычисления продолжают до тех пор, пока не будет достигну­то условие 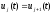, при котором управления на двух соседних циклах обращения к операциям 2-10 совпадают и характеризуются одним и тем же значением критерия качества. Это управление принимается за окончательное решение задачи .
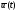