
- •1.Системний підхід до проектування інформаційних систем 5
- •2.Проектування елементів ісм 16
- •Анотація
- •Системний підхід до проектування інформаційних систем
- •Суть та характеристика системного підходу
- •Процес створення іс на основі системного підходу
- •Особливості проектування іс на сучасному етапі
- •Проектування елементів ісм
- •Загальна характеристика
- •Функціональна підсистема
- •Система опрацювання даних
- •Інформаційне забезпечення
- •Програмне забезпечення
- •Технічне забезпечення
- •Організаційна підсистема
- •Опис процесу реалізації задачі
- •Розрахунок економічної ефективності комп’ютеризації
- •Висновки до розділу 2
- •Висновки
- •Список використаної літератури
-
Опис процесу реалізації задачі
За допомогою точкового графіка малюємо кореляційні поля для різних типів зв’язку:



Далі проводимо розрахунок параметрів рівняння лінійної регресії. Таке рівняння має вигляд Y = a*X + b. Виділяємо область клітинок розміром 5 рядків на 2 стовбці, тоді вводимо функцію “ЛИНЕЙН”. У полях “Известные_значения_у” і “Известные_значения_х” даємо посилання відповідно D7:D28і С7:С28, наступні два поля приймають значення по одиниці.

Для того щоб поширити дану функцію на весь масив після введення всіх значень потрібно натиснути Ctrl+Shift+Enter.
В результаті ми отримали таблицю з параметрами регресії. Пояснення до даної таблиці знаходиться в таюлиці
Табл. Параметри регресії
|
Коефцієнт a |
Коефіцієнт b |
|
Стандартна помилка m0 |
Стандартна помилка mh |
|
Коефіцієнт детермінації Rxy |
Середньоквадратичне відхилення y |
|
F-статистика |
Ступені свободи n-2 |
|
Регресійна сума квадратів Sn2 |
Залишкова сума квадратів Sn2 |
Отже, коефіцієнт регресії знаходиться в клітинці L8 і становить 0,974. Параметри для даного рівняння приймуть такі значення: a = 12,743, b = 0,075.

Проводимо розрахунок параметрів рівняння степеневої регресії. Таке рівняння матиме вигляд Y = a * X^b. Для того щоб знову використати функцію “ЛИНЕЙН” замість X і Y потрібно взяти натуральні логарифми цих значень. Знову виділяємо область клітинок розміром 5 рядків на 2 стовбці, тоді вводимо функцію “ЛИНЕЙН”. У полях “Известные_значения_у” і “Известные_значения_х” тепер даємо посилання відповідно LN(D7:D28) і LN(C7:C28), наступні два поля так само приймають значення по одиниці.

Знову поширюємо функцію на весь масив.
Результатом є таблиця з параметрами регресії. Коефіцієнт регресії знаходиться в клітинці L23 і становить 0,946. Параметр b для даного рівняння становитиме 0,822, а параметр a знаходиться за формулою =EXP(M6) і становить 0,211.

Далі проводимо розрахунок параметрів рівняння експоненційної регресії – Y=a*e^(b*X). Для розрахунку показників експоненційної регресії можна знову застосувати функцію “ЛИНЕЙН”. Проте замість значень Х потрібно підсавляти натуральний логарифм цих значень. Виділяємо область клітинок розміром 5 рядків на 2 стовбці та вводимо функцію “ЛИНЕЙН”. У полях “Известные_значения_у” і “Известные_значения_х” даємо посилання LN(D7:D28) і C7:C28 відповідно, наступні два поля знову приймають значення по одиниці.

Поширюємо дану функцію на весь масив і отримуєм таблицю параметрів регресії.
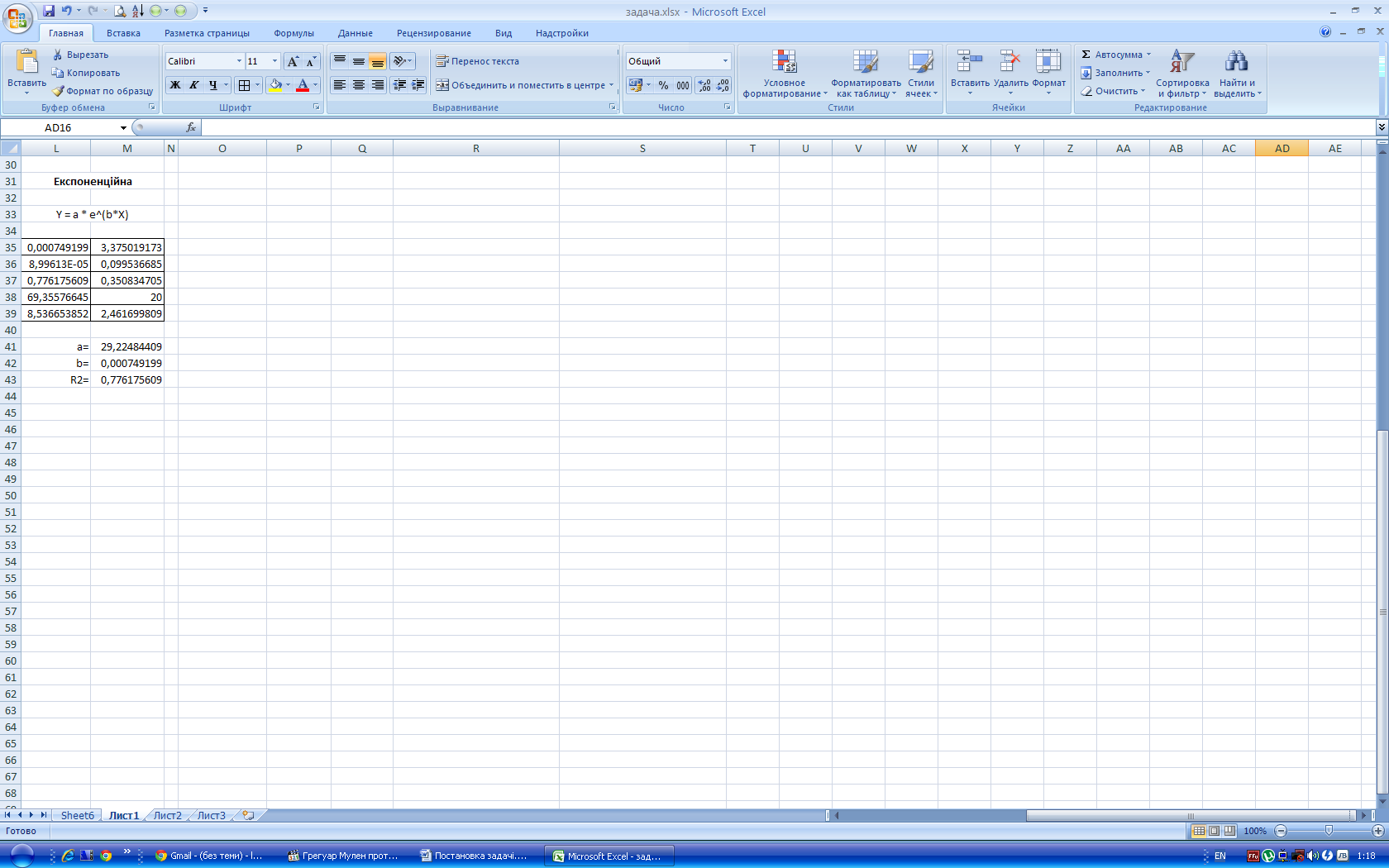
В даному випадку коефіцієнт регресії знаходиться в клітинці L37 і становить 0,776. І це значення є найнижчим. Параметр b для даного рівняння становитиме 0,0007, а параметр a знаходиться так само як і при попередній залежності – за формулою =EXP(M25) і становить 29,224.
Порівнявши коефіцієнти детермінації ми визначили, що найбільшого значення цей показник досяг при лінійній залежності. Отже, найкращою формою регресійної залежності між показниками можна вважати лінійну залежність.
