
- •1. Перенос энергии электромагнитной волной, вектор Пойтинга, интенсивность. Шкала электромагнитных волн.
- •2. Основные законы геометрической оптики. Принцип Ферма. Оптический путь. Принцип Гюйгенса.
- •3. Интерференция и когерентность. Интерференция от двух точечных излучателей на примере опыта Юнга.
- •4.Интерференция по методу деления волнового фронта: бипризма Френеля, зеркало Ллойда.
- •5.Интерференция света в плоскопараллельных пластинах. Линии равного наклона и равной толщины.
- •6. Принцип Гюйгенса-Френеля. Зоны Френеля. Метод векторных диаграмм.
- •7.Дифракция Френеля от простейших преград. Зонная пластинка.
- •Дифракция от диска
- •8. Дифракция Фраунгофера от щели (случай нормального падения света). Расчет интенсивности методом векторных диаграмм.
- •9. Количественный критерий вида дифракции.
- •10. Дифракция Фраунгофера на решетке (случай нормального падения света).
- •11.Дифракционная решетка как спектральный прибор: угловая дисперсия, разрешающая сила, критерий Рэлея.
- •12.Поляризация света. Виды поляризации. Закон Малюса.
- •Вопрос 13. Поляризация света при отражении и преломлении. Закон Брюстера.
- •14. Дисперсия света. Фазовая и групповая скорости.
- •15. Абсолютно черное тело. Законы излучения.
- •Закон Кирхгофа.
- •Закон Стефана-Больцмана.
- •Закон смещения Вина.
- •16. Тепловое излучение. Закон Кирхгофа.
- •19. Тормозное рентгеновское излучение.
- •20. Фотоэлектрический эффект.
- •21. Рассеяние рентгеновских лучей. Эффект Комптона.
- •22. Модель атома Резерфорда. Опыты по рассеиванию α-частиц.
- •23. Закономерности в атомных спектрах. Формула Бальмера.
- •24. Постулаты Бора. Правило квантования орбит.
- •25. Элементарная боровская теория водородного атома.
- •26.Волновые свойства микрочастиц. Гипотеза Луи де Бройля.
- •27.Соотношение неопределенностей Гейзенберга.
- •28. Свойства волновой функции. Принцип суперпозиции.
- •29. Уравнение Шредингера. Квантование энергии частиц.
- •Вопрос 30. Частица в потенциальной яме.
- •31.Атома водорода. Квантовые числа.
- •33. Металлы, диэлектрики и полупроводники с точки зрения зонной теории.
9. Количественный критерий вида дифракции.

Дифракция Френеля – дифракционная картина, которая наблюдается на небольшом расстоянии от препятствия, по условиям, когда основной вклад в интерференционную картину дают границы экрана.
Дифракция Фраунгофера – случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды.
10. Дифракция Фраунгофера на решетке (случай нормального падения света).
Дифракционной
решеткой называется совокупность
равноотстоящих щелей.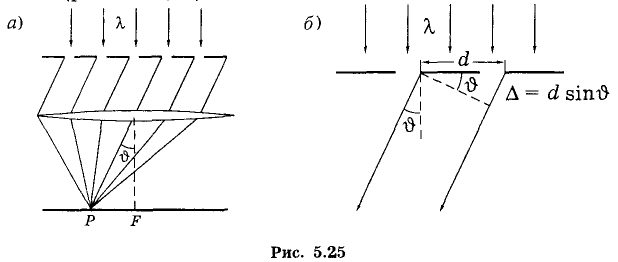
d – период решетки.
N – число щелей.
Ширина каждой щели – b.
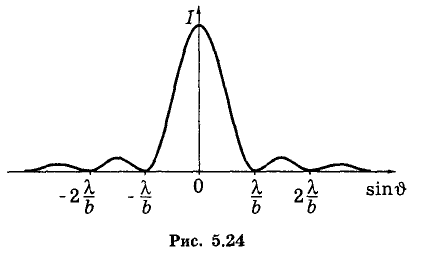
Пусть плоская монохроматическая световая волна падает на решетку нормально. Каждая из щелей в отдельности давала бы в фокальной плоскости объектива дифракционную картину, показанную на рис. 5.24. И такие картины от всех щелей в отсутствие когерентности точно накладывались бы друг на друга, независимо от их положения. Интенсивности при этом складывались бы, и мы получили бы при наличии N щелей дифракционную картину как от одной щели, но усиленную в N раз.
При освещении же решетки когерентным светом, световые волны от всех щелей интерферируют друг с другом, и дифракционная картина резко меняется. Мы будем наблюдать систему достаточно узких максимумов.
Главные максимумы. В середину дифракционно-интерференционной картины когерентные колебания от всех щелей приходят в фазе. Это значит, что если амплитуда от одной щели равна А1, а число щелей в решетке N, то результирующая амплитуда А и соответствующая ей интенсивность I будут определяться формулами
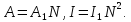
Такой
же результат получается и при углах
дифракции ϑ,
для которых оптическая разность хода
 колебаний от соседних щелей (см. рис.
5.25, б) равна целому числу длин волн:
колебаний от соседних щелей (см. рис.
5.25, б) равна целому числу длин волн:
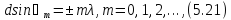
где знаки «±» следуют из симметрии дифракционной картины относительно нормали к решетке (ϑ0 = 0): при знаке «+» угол ϑт>0, а при знаке «-» угол ϑт<0.
В направлениях ϑт , определяемых этим уравнением, возникают максимумы, интенсивность которых в N2 раз превосходят интенсивность от каждой щели в том же направлении. Их называют главными максимумами m-го порядка, а уравнение (5.21) — условием главных максимумов. Именно главные максимумы и представляют особый практический интерес. Как мы увидим далее, они получаются тем более узкими и резкими, чем большее число N штрихов содержит решетка.
Интерференционные
минимумы.
Для выяснения дальнейших деталей
фраунгоферовой дифракционной картины
воспользуемся векторной диаграммой,
которая позволит легко найти и
результирующую амплитуду А
колебаний,
приходящих в произвольную точку Р
фокальной
плоскости объектива (см. рис. 5.25).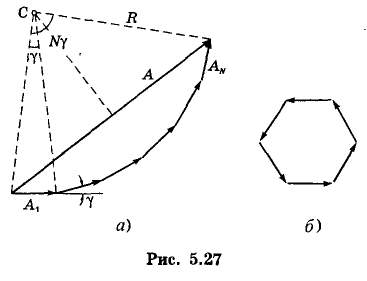
Векторная
диаграмма в нашем случае представляет
собой цепочку векторов-амплитуд
когерентных колебаний, приходящих
в точку Р от каждой из N
щелей: A1
А2,...,
AN
(рис.
5.27). По модулю эти векторы одинаковы, и
каждый следующий отстает от предыдущего
(или опережает, это не существенно) по
фазе на один и тот же угол γ.
Этот угол связан с оптической разностью
хода
 соответствующих лучей от соседних щелей
известным соотношением
соответствующих лучей от соседних щелей
известным соотношением
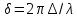 ,
т. е. в нашем случае — при нормальном
падении света на решетку
,
т. е. в нашем случае — при нормальном
падении света на решетку
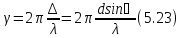
где d – период решетки (см.рис.5.25.б).
Теперь проследим, как будет вести себя эта цепочка векторов (а значит и ее замыкающая А) при удалении точки Р от фокуса F (см. рис. 5.25, а), т. е. с ростом угла дифракции ϑ.
Ясно, что при этом будет увеличиваться разность фаз γ между колебаниями от соседних щелей, и цепочка векторов будет постепенно закручиваться. Первый раз она замкнется и вектор А обратится в нуль, когда угол Nγ станет равным 2π — это непосредственно видно из рис. 5.27, б.
При
дальнейшем росте угла ϑ, а значит,
разности фаз γ
и
Nγ,
цепочка
будет периодически то распрямляться
(главные максимумы, А=макс), то замыкаться
(интерференционные минимумы, А
=
0). Последнее будет происходить при
значениях угла Nγ
кратных
2π:
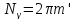 (5,24),
где
m’
принимает
целочисленные значения, кроме 0, N,
2N…,
при
которых цепочка распрямляется, и мы
получаем главные максимумы.
(5,24),
где
m’
принимает
целочисленные значения, кроме 0, N,
2N…,
при
которых цепочка распрямляется, и мы
получаем главные максимумы.
Подставив в (5.24) значение γ из формулы (5,23) получим:
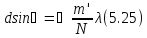
Это выражение представляет собой условие для интерференционных минимумов (при целочисленных значениях т , кроме 0, N, 2N,..). Оно же содержит и условие для главных максимумов (при т' = 0, N, 2N, ...). Между двумя соседними главными максимумами расположены N-1 интерференционных минимумов. А между последними, в свою очередь, — добавочные максимумы, интенсивность которых при достаточно большом числе N штрихов решетки пренебрежимо мала (как мы увидим далее, она составляет не более 5% от интенсивности главных максимумов).
Лекции:
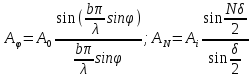
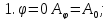
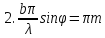
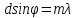 – условие
главных максимумов
– условие
главных максимумов
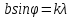 – условие
минимума одной щели
– условие
минимума одной щели
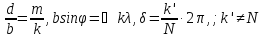
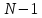 – добавочных
минимумов,
– добавочных
минимумов,
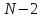 – добавочных максимумов
– добавочных максимумов
