
- •1. Перенос энергии электромагнитной волной, вектор Пойтинга, интенсивность. Шкала электромагнитных волн.
- •2. Основные законы геометрической оптики. Принцип Ферма. Оптический путь. Принцип Гюйгенса.
- •3. Интерференция и когерентность. Интерференция от двух точечных излучателей на примере опыта Юнга.
- •4.Интерференция по методу деления волнового фронта: бипризма Френеля, зеркало Ллойда.
- •5.Интерференция света в плоскопараллельных пластинах. Линии равного наклона и равной толщины.
- •6. Принцип Гюйгенса-Френеля. Зоны Френеля. Метод векторных диаграмм.
- •7.Дифракция Френеля от простейших преград. Зонная пластинка.
- •Дифракция от диска
- •8. Дифракция Фраунгофера от щели (случай нормального падения света). Расчет интенсивности методом векторных диаграмм.
- •9. Количественный критерий вида дифракции.
- •10. Дифракция Фраунгофера на решетке (случай нормального падения света).
- •11.Дифракционная решетка как спектральный прибор: угловая дисперсия, разрешающая сила, критерий Рэлея.
- •12.Поляризация света. Виды поляризации. Закон Малюса.
- •Вопрос 13. Поляризация света при отражении и преломлении. Закон Брюстера.
- •14. Дисперсия света. Фазовая и групповая скорости.
- •15. Абсолютно черное тело. Законы излучения.
- •Закон Кирхгофа.
- •Закон Стефана-Больцмана.
- •Закон смещения Вина.
- •16. Тепловое излучение. Закон Кирхгофа.
- •19. Тормозное рентгеновское излучение.
- •20. Фотоэлектрический эффект.
- •21. Рассеяние рентгеновских лучей. Эффект Комптона.
- •22. Модель атома Резерфорда. Опыты по рассеиванию α-частиц.
- •23. Закономерности в атомных спектрах. Формула Бальмера.
- •24. Постулаты Бора. Правило квантования орбит.
- •25. Элементарная боровская теория водородного атома.
- •26.Волновые свойства микрочастиц. Гипотеза Луи де Бройля.
- •27.Соотношение неопределенностей Гейзенберга.
- •28. Свойства волновой функции. Принцип суперпозиции.
- •29. Уравнение Шредингера. Квантование энергии частиц.
- •Вопрос 30. Частица в потенциальной яме.
- •31.Атома водорода. Квантовые числа.
- •33. Металлы, диэлектрики и полупроводники с точки зрения зонной теории.
5.Интерференция света в плоскопараллельных пластинах. Линии равного наклона и равной толщины.
Пусть на прозрачную плоскопараллельную пластинку падает плоская монохроматическая световая волна, направление распространения которой показано падающим лучом на рис. В результате отражений от обеих поверхностей пластинки исходная волна расщепится на две, что и показано лучами 1 и 2. Амплитуды этих волн мало отличаются друг от друга.
Оптическую
разность хода волн 1
и 2 определим,
согласно рис, как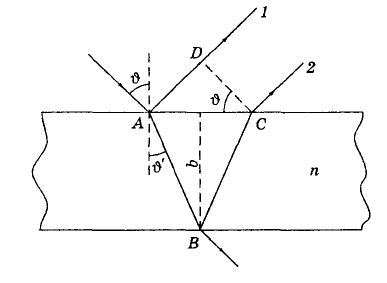
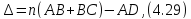
где
п
—
показатель преломления вещества
пластинки.
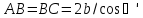 и
и
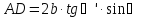 ,
b
– толщина
пластинки. Подставим в (4.29):
,
b
– толщина
пластинки. Подставим в (4.29):
 При отражении от верхней поверхности
пластинки происходит скачок фазы на π
у отраженной волны, т. е., потеря» полуволны
(±λ/2)
При отражении от верхней поверхности
пластинки происходит скачок фазы на π
у отраженной волны, т. е., потеря» полуволны
(±λ/2)
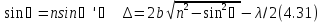
(здесь можно было написать и +λ/2, но это не существенно).
Если отраженные волны 1 и 2 когерентны, то максимумы отражения будут наблюдаться при условии

где т – целое число (порядок интерференции).
При
падении плоской световой волны на
плоскопараллельную тонкую пластинку
интенсивность отраженного света зависит
от угла падения. Изменяя этот угол, мы
будем наблюдать чередование максимумов
и минимумов отраженного света. Это можно
использовать для получения интерференционной
картины в виде привычной системы полос.
Достаточно использовать в качестве
падающего рассеянный монохроматический
свет (он содержит волны, падающие на
пластинку одновременно под разными
углами), а на пути отраженного света
поставить линзу и в ее фокальной плоскости
экран. См. рис.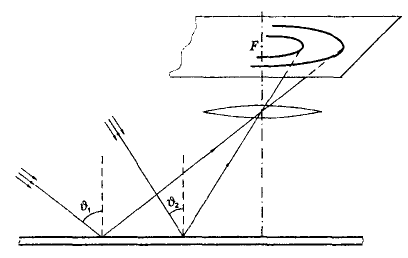
Максимумы на экране будут располагаться в местах, соответствующих условию (4.32). Полоса данного порядка интерференции обусловлена светом, падающим на пластинку под одним и тем же углом ϑ, но с разных направлений. Поэтому такие полосы называют полосами равного наклона. При расположении линзы как показано на рисунке, эти полосы имеют вид концентрических колец с центром в ее фокусе F. Порядок интерференции т растет с уменьшением угла падения ϑ, и в центре картины он максимален.
Клиновидные пластинки. Пусть стеклянная пластинка имеет форму клина с углом раствора α«1, и на нее падает плоская монохроматическая световая волна. Теперь отраженные от поверхностей клина световые волны будут распространяться не в одном направлении, а под некоторым углом.
Выясним
прежде всего, где будет локализована
интерференционная картина. Это проще
всего сделать с помощью рис, на котором
показано, что происходит с областью
когерентности после расщепления волны
при отражении от поверхностей клина.
Ясно, что при небольших значения lког
и hког,
область перекрытия когерентных частей
отраженных волн локализована в
основном вблизи поверхности клина и
становится все более узкой по мере
перемещения в сторону утолщения клина,
постепенно исчезая совсем (рис. 4.19). На
рисунке область локализации несколько
затемнена.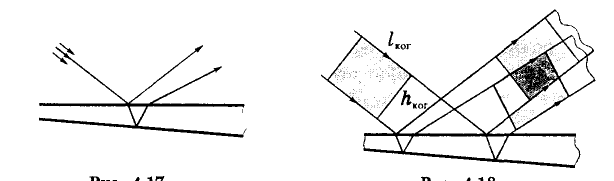
Так как разность хода лучей, отразившихся от различных участков клина, неодинакова, в области локализации интерференции появятся светлые и темные полосы, параллельные ребру клина. Каждая из таких полос возникает в результате отражений от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины.
