
- •1. Перенос энергии электромагнитной волной, вектор Пойтинга, интенсивность. Шкала электромагнитных волн.
- •2. Основные законы геометрической оптики. Принцип Ферма. Оптический путь. Принцип Гюйгенса.
- •3. Интерференция и когерентность. Интерференция от двух точечных излучателей на примере опыта Юнга.
- •4.Интерференция по методу деления волнового фронта: бипризма Френеля, зеркало Ллойда.
- •5.Интерференция света в плоскопараллельных пластинах. Линии равного наклона и равной толщины.
- •6. Принцип Гюйгенса-Френеля. Зоны Френеля. Метод векторных диаграмм.
- •7.Дифракция Френеля от простейших преград. Зонная пластинка.
- •Дифракция от диска
- •8. Дифракция Фраунгофера от щели (случай нормального падения света). Расчет интенсивности методом векторных диаграмм.
- •9. Количественный критерий вида дифракции.
- •10. Дифракция Фраунгофера на решетке (случай нормального падения света).
- •11.Дифракционная решетка как спектральный прибор: угловая дисперсия, разрешающая сила, критерий Рэлея.
- •12.Поляризация света. Виды поляризации. Закон Малюса.
- •Вопрос 13. Поляризация света при отражении и преломлении. Закон Брюстера.
- •14. Дисперсия света. Фазовая и групповая скорости.
- •15. Абсолютно черное тело. Законы излучения.
- •Закон Кирхгофа.
- •Закон Стефана-Больцмана.
- •Закон смещения Вина.
- •16. Тепловое излучение. Закон Кирхгофа.
- •19. Тормозное рентгеновское излучение.
- •20. Фотоэлектрический эффект.
- •21. Рассеяние рентгеновских лучей. Эффект Комптона.
- •22. Модель атома Резерфорда. Опыты по рассеиванию α-частиц.
- •23. Закономерности в атомных спектрах. Формула Бальмера.
- •24. Постулаты Бора. Правило квантования орбит.
- •25. Элементарная боровская теория водородного атома.
- •26.Волновые свойства микрочастиц. Гипотеза Луи де Бройля.
- •27.Соотношение неопределенностей Гейзенберга.
- •28. Свойства волновой функции. Принцип суперпозиции.
- •29. Уравнение Шредингера. Квантование энергии частиц.
- •Вопрос 30. Частица в потенциальной яме.
- •31.Атома водорода. Квантовые числа.
- •33. Металлы, диэлектрики и полупроводники с точки зрения зонной теории.
29. Уравнение Шредингера. Квантование энергии частиц.
Ψ – функция характеризующая состояние микрочастицы.
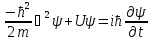 m
– масса частицы, i – мнимая
единица,
m
– масса частицы, i – мнимая
единица,
 – оператор Лапласа
– оператор Лапласа
 U
– функция координат и времени, градиент
которой, взятый с обратным знаком,
определяет силу, действующую на частицу.
U
– функция координат и времени, градиент
которой, взятый с обратным знаком,
определяет силу, действующую на частицу.
Если
силовое поле стационарно, то U
не зависит явно от времени ψ(x,y,z,t)
= ψ(x,y,z)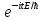 ,
E - полная энергия частицы
,
E - полная энергия частицы
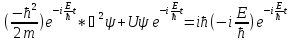

 – уравнение Шредингера для
стационарных состояний.
– уравнение Шредингера для
стационарных состояний.
Квантование энергии частиц
Квадрат
модуля ψ-функции определяет вероятность
dP того, что частица будет
обнаружена в пределах объёма dV:
dP=|ψ|2dV,
P=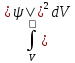 ;
;
 – условие нормировки.
– условие нормировки.
ψ-функция должна быть однозначной, гладкой, непрерывной и конечной.
Потенциальная Яма
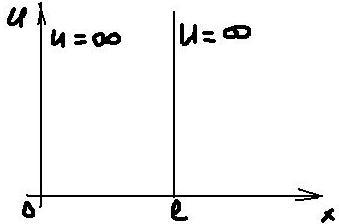
Частица движется вдоль оси X и движение ограничено x=0 и x=l
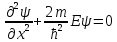 .
Решения, соответствующие собственным
значениям E, называются
собственными функциями. В этой области
U=0. Обозначим
.
Решения, соответствующие собственным
значениям E, называются
собственными функциями. В этой области
U=0. Обозначим
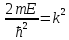 .
Получим,
.
Получим,
 .
Решение уравнения имеет вид
.
Решение уравнения имеет вид
 ;
;
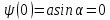

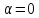 ;
;
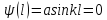 ,
kl= ± πn,
n=1,2,3,…
,
kl= ± πn,
n=1,2,3,…
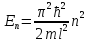 ,
n=1,2,3,…
,
n=1,2,3,… Спектр энергии дискретен
Спектр энергии дискретен
Вопрос 30. Частица в потенциальной яме.
Одномерная потенциальная яма. Рассмотрим
частицу, находящуюся в одномерной
прямоугольной потенциальной яме с
бесконечно высокими стенками. В этом
случае потенциальная энергия
частицы 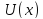 имеет
вид
имеет
вид
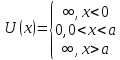 ,
,
т.е.
внутри ямы (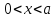 )
потенциальная энергия
)
потенциальная энергия 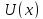 постоянна
и равна нулю, а вне ямы обращается в
бесконечность
постоянна
и равна нулю, а вне ямы обращается в
бесконечность
Запишем уравнение Шредингера для одномерного движения частицы вдоль оси x
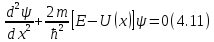
В силу непрерывности волновая функция
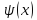 должна
обращаться в нуль и на границах ямы: при
x=0 и при x=a.
Таким образом, задача о движении частицы
в яме сводится к решению уравнения
должна
обращаться в нуль и на границах ямы: при
x=0 и при x=a.
Таким образом, задача о движении частицы
в яме сводится к решению уравнения

с граничными условиями

Введем
обозначение
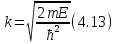
При этом уравнение (4.12)
принимает вид хорошо известного из
теории колебаний уравнения
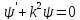 решение которого есть
решение которого есть
 (4.14)
(4.14)
Используя граничное условие
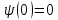 ,
получаем
,
получаем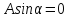 откуда
следует, что
откуда
следует, что
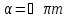 ,
где m=0,1,2,.... без
потери общности можно считать, что
,
где m=0,1,2,.... без
потери общности можно считать, что
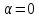 .
.
Второе граничное условие  приводит
к соотношению
приводит
к соотношению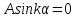 которое
для
которое
для
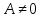 выполняется
при
выполняется
при
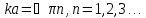 (4.15)
(4.15)
Подставляя (4.13) в (4.15) , приходим к выражению для полной энергии частицы, движущейся в потенциальной яме с непроницаемыми стенками

31.Атома водорода. Квантовые числа.
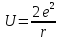 -
потенциальная энергия электрона, r
– расстояние от электрона до ядра.
-
потенциальная энергия электрона, r
– расстояние от электрона до ядра.
Энергия
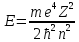 ,
n=1,2,3,…
,
n=1,2,3,…
n – главное квантовое число, совпадает в номером уровня энергии, n=1,2,3,…
l – азимутное квантовое число, l=0,1,2,3,…,n-1
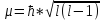 – момент импульса
– момент импульса
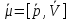
m
– магнитное квантовое число,
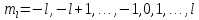
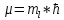 – проекция момента импульса на выбранное
направление
– проекция момента импульса на выбранное
направление
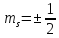 ,
,
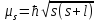 – спиновой момент
– спиновой момент
Принцип Паули
В одном атоме не может быть двух электронов с одинаковой совокупностью квантовых чисел
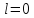 s
- состояние
s
- состояние
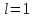 p
- состояние
p
- состояние
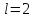 d
- состояние
d
- состояние
 f
– состояние, затем идут g,h
и так далее уже по алфавиту
f
– состояние, затем идут g,h
и так далее уже по алфавиту
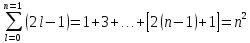 – число различных состояний
– число различных состояний
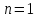 – 2 электрона – k - оболочка
– 2 электрона – k - оболочка
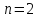 – 8 электронов – L - оболочка
– 8 электронов – L - оболочка
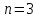 – 18 электронов – M -
оболочка
– 18 электронов – M -
оболочка
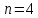 – 32 электрона – N - оболочка
– 32 электрона – N - оболочка
 – 50 электронов – Q –
оболочка
– 50 электронов – Q –
оболочка
Для полностью заполненной электронной оболочки суммарный орбитальный и спиновый момент равен нулю. Свойства элемента зависят от количества электронов и их расположения.
|
слой |
n |
l |
ml |
ms |
Оболочка |
|
K |
1 |
0 |
0 |
↑↓ |
K(1s) |
|
L |
2 |
0 |
0 |
↑↓ |
L1(2s) |
|
-1 |
↑↓ |
||||
|
1 |
0 |
↑↓ |
L2(2p) |
||
|
1 |
↑↓ |
||||
|
M |
3 |
0 |
0 |
↑↓ |
M1(3s) |
|
1 |
-1 |
↑↓ |
M2(3p) |
||
|
0 |
|||||
|
1 |
|||||
|
2 |
-2 |
↑↓ |
M3(3d) |
||
|
-1 |
|||||
|
0 |
|||||
|
1 |
|||||
|
2 |
