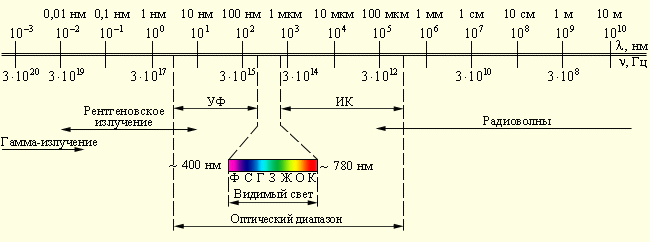
1. Перенос энергии электромагнитной волной, вектор Пойтинга, интенсивность. Шкала электромагнитных волн.

Электромагнитная волна - процесс распространения электромагнитного поля в пространстве.

Электромагнитная волна представляет собой процесс последовательного, взаимосвязанного изменения векторов напряжённости электрического и магнитного полей, направленных перпендикулярно лучу распространения волны, при котором изменение электрического поля вызывает изменения магнитного поля, которые, в свою очередь, вызывают изменения электрического поля.

Электромагнитные волны переносят энергию. Согласно формуле j=ωv плотность потока энергии можно получить, умножив плотность энергии на скорость волны.

В обычной изотропной среде с проницаемостями ε и μ плотность энергии электромагнитного поля равна сумме плотностей энергии электрического и магнитного полей:

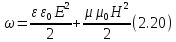
В данной среде справедливо соотношение 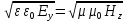, а это означает, что плотность электрической энергии в бегущей волне равна плотности магнитной энергии. Поэтому (2.20) можно записать так: (2.21), где v – скорость волны, .

Умножив ω на v, получим плотность потока энергии S=ωv=EH (2.22).

Векторы E и H взаимно ортогональны и образуют с направлением распространения волны правовинтовую систему. Значит, направления [EH] совпадают с направлением переноса энергии, а модуль этого вектора равен EH. Поэтому вектор плотности потока электромагнитной энергии S можно представить как S=[EH]. Вектор S называют вектором Пойтинга. В случае бегущей гармонической электромагнитной волны плотность энергии согласно (2.21) равна . Плотность же потока энергии, как следует из 2.22, где учтено, что скорость v определяется формулой .

Интенсивность I такой волны равна, по определению, среднему значению плотности энергии: I=<S>. Принимая во внимание, что при усреднении среднее значение квадрата косинуса равно 1/2, получим 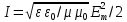. Обратим внимание, что I пропорционально квадрату амплитуды, I~.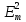

В стоячей электромагнитной волне энергия переходит из чис­то электрической, имеющей максимумы в пучностях Е, в маг­нитную с максимумами в пучностях вектора Н, т. е. смещенным в пространстве на λ/4. Это аналогично поведению гармоническо­го осциллятора, например математического маятника, где энер­гия переходит из чисто потенциальной (в крайнем положении) в кинетическую (в положении равновесия), и наоборот.

Отметим, что если волна представляет собой наложение двух бегущих волн со взаимно перпендикулярными плоскостями по­ляризации (направлением колебаний вектора Е), то ее интенсив­ность независимо от особенностей этих волн будет равна сумме интенсивностей складываемых волн. Действительно, Е = E₁+E₂, а интенсивность 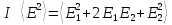. Поскольку Е₁ | Е₂, скалярное произведение E₁E₂ = 0, и мы имеем I = I₁ +I₂.

Волны	Длина волны λ
Электромагнитные	1015–106,5
Инфракрасные	107,5–104
Видимый спектр	104–103
Ультрафиолет	103–101,5
Рентген	102–10-1,5
γ-лучи	10-0,5-…