информ.лаба №11. 1 курс .игхту

ЛАБОРАТОРНАЯ РАБОТА №11

Многомерный поиск. Линейное программирование

1 ЧАСТЬ.

	x1	x2
искомые значения х	5	7
	кф. При х1	кф. При х2	своб-й член	формула
R	2,8	3,6	0,8	40
ограничение 1	1	0,5	5	8,5
ограничение 2	1	0	1	5
ограничение 3	0	1	7	7
ограничение 4	1	1	12	12
ограничение 5	-2	4	-9	18

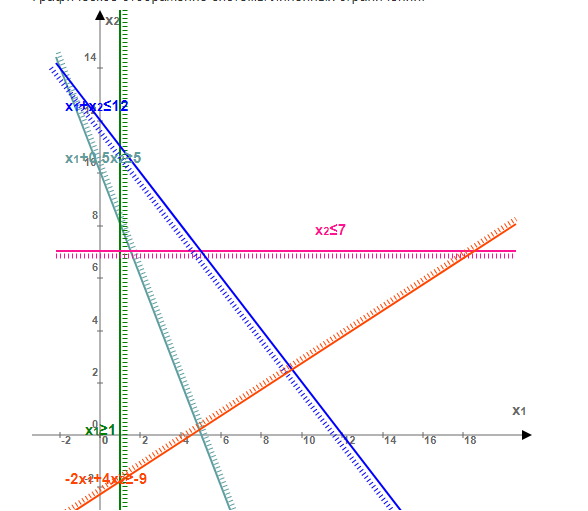
Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (2.8;3.6). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.

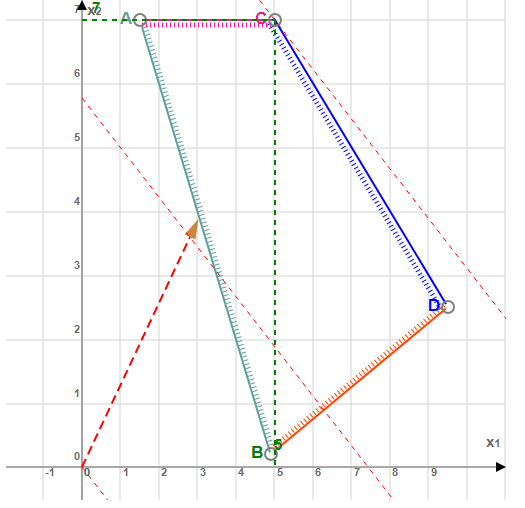
Прямая F(x) = const пересекает область в точке C. Так как точка C получена в результате пересечения прямых  x₂=7 и x₁+x₂=12 , то ее координаты удовлетворяют уравнениям этих прямых. Решив систему уравнений, получим: x₁ = 5, x₂ = 7 Откуда найдем максимальное значение целевой функции: F(X) = 2.8*5 + 3.6*7 + 0.8 = 40

Вывод: данные расчитанные с помощью EXCEL совпадают с данными расчитанными графическим методом

Часть 2

	x1	x2
искомые значения х	23,75	9,7917
	кф. При х1	кф. При х2	своб-й член	формулы
R	25	40	0	985,4167
ограничение 1	3	6	130	130
ограничение 2	14	12	450	450

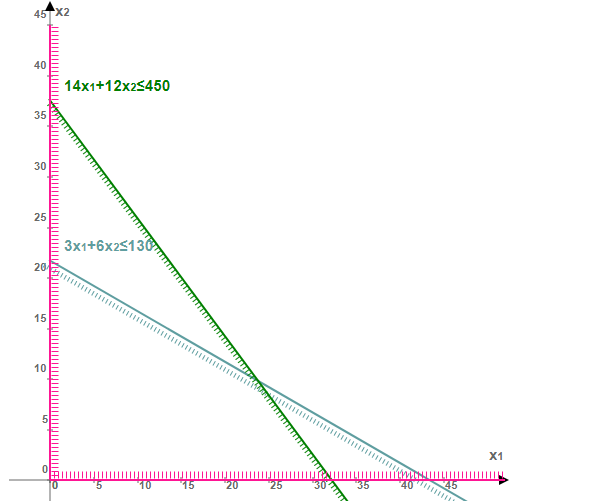
Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (25;40). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.

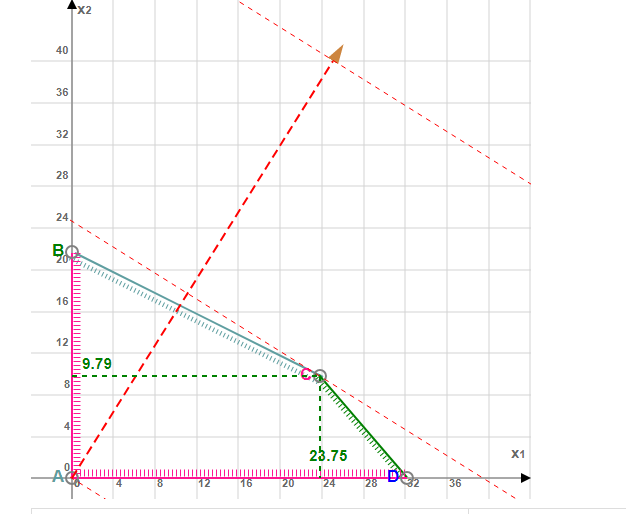
Прямая F(x) = const пересекает область в точке C. Так как точка C получена в результате пересечения прямых   3x₁+6x₂=130 и 14x₁+12x₂=450, то ее координаты удовлетворяют уравнениям этих прямых. Решив систему уравнений, получим: x₁ = 23.75, x₂ = 9.7917 Откуда найдем максимальное значение целевой функции: F(X) = 25*23.75 + 40*9.7917 = 985.4167

Ответы на вопросы:

1. продукта 1 следует производить – 25

2. продукта 2 следует производить – 40

3. максимальная прибыль= 985.4167

	x1	x2
искомые значения х	23,875	9,7292
	кф. При х1	кф. При х2	своб-й член	формулы
R	25	40	0	986,0417
ограничение 1	3	6	130	130
ограничение 2	14	12	451	451

986.0417-985.4167=0.625

Если резерв рабочего дня увеличить на 1 чел/час, то прибыль увеличиться на 0.625