информ.лаба №8. 1 курс .игхту

ЛАБОРАТОРНАЯ РАБОТА №8.

вариант № 4

«АНАЛИЗ МОДЕЛЕЙ В ВИДЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ»

Задание: Локализовать наименьший положительный корень уравнения 4x  5ln x  5  0 и уточнить его значение с точностью до ε=0,0001 двумя методами.

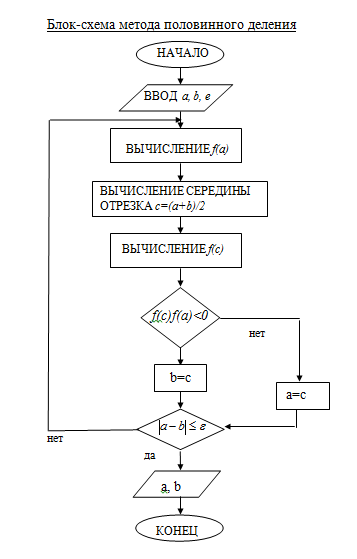
1. методом половинного деления

2. методом комбинированным: хорд и касательных.

Теоретическое введение

1. Уточнение корней методом половинного деления

Пусть корень уравнения 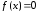отделен на отрезке [a, b], т.е. f(a)f(b)<0 и f ’(x) сохраняет знак (рис. 2.6.).

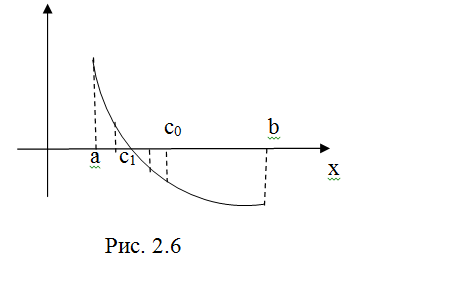
В качестве начального приближения корня возьмем точку c₀ – середину отрезка: 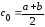. Если f(с₀)=0, то c₀ – искомый корень уравнения, если 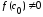, то из двух отрезков [a, c₀] и [c₀, b] выбираем тот, на концах которого функция принимает значение разных знаков.

Новый отрезок опять делим пополам и далее поступаем аналогично вышеизложенному. Длина каждого нового отрезка вдвое меньше длины предыдущего отрезка, т.е. за n шагов сократится в 2ⁿ раз.

Вычисления прекращаем, если длина отрезка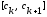 станет меньше заданной погрешности , т.е. .

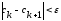2. Комбинированный метод хорд и касательных

Методы хорд и касательных дают приближения корня с разных сторон. Поэтому их часто применяют в сочетании друг с другом, тогда уточнение корня происходит быстрее.

Пусть дано уравнение f(x)=0, корень отделен на отрезке [a, b].

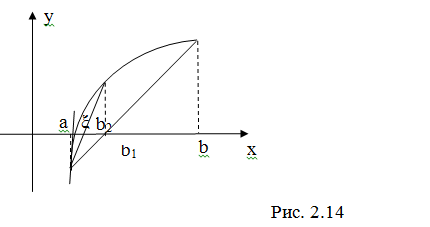
Рассмотрим случай, когда f ‘(x) f ’’(x)>0 (рис. 2.13)

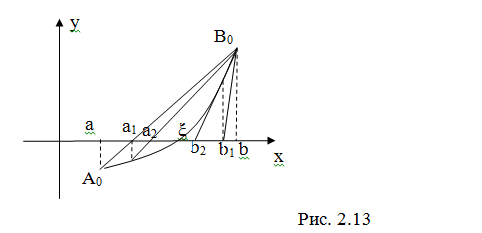
В этом случае метод хорд дает приближенное значение корня с недостатком (конец b неподвижен), а метод касательных – с избытком (за начальное приближение берем точку b).

Тогда вычисления следует проводить по формулам:

; .

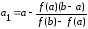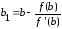Теперь корень ξ заключен в интервале [a₁, b₁].

Применяя к этому отрезку комбинированный метод, получим:

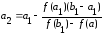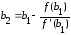; и т.д.

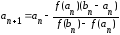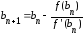; (2.6)

Если же f ‘(x) f ’’(x)<0 (рис. 2.14), то рассуждая аналогично, получим следующие формулы для уточнения корня уравнения:

; .

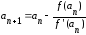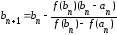Вычислительный процесс прекращается, как только .

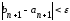Выполнение работы

1. Локализация корня

Определим графически корень уравнения, для этого построим график функции y=4x  5ln x  5

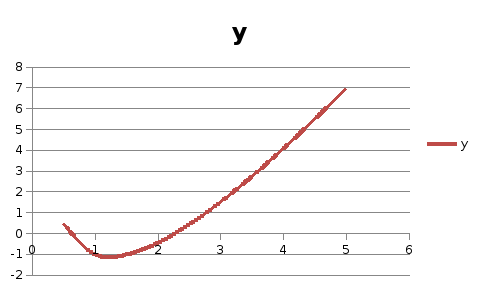
Из графика следует , что корень находится на отрезке [0,5;1]

2. Метод половинного деления

1-ая итерация

А= 0,5

Б=1

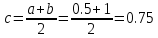
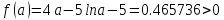
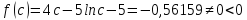
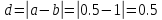>0.0001 cледовотельно точность не достигнута, и необходимо продолжить расчеты

так как f(a)*F(c)<0 то следующий интервал для расчетов (0,5;0,75)

2-я итерация

А= 0,5

Б=0,75

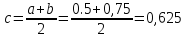
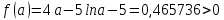
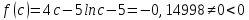
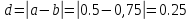>0.0001 cледовотельно точность не достигнута, и необходимо продолжить расчеты

так как f(a)*F(c)<0 то следующий интервал для расчетов (0,5;0,625)

3-я итерация

А= 0,5

Б=0,625

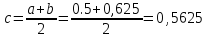
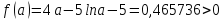
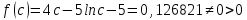
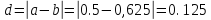>0.0001 =>точность не достигнута, и необходимо продолжить расчеты

так как f(a)*F(c)<0 то следующий интервал для расчетов (0,5;0,5625)

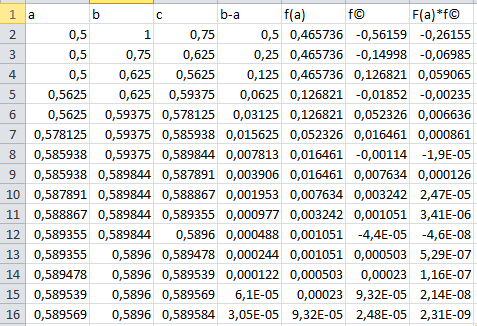
Ответ: х=0,5896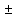0,0001

2. Метод комбинированный: хорд и касательных.

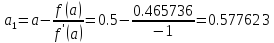(метод касательных)

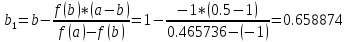(метод хорд)

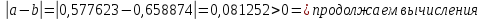
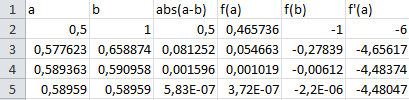
Ответ:x=0,5896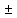0,0001