
§35. Центральная предельная теорема.
Случайная величина X называется центрированной и нормированной, если ее математическое ожидание равно нулю, а дисперсия – единице.
Любую случайную
величину X
с конечной дисперсией
![]() и математическим ожиданием
и математическим ожиданием
![]() можно центрировать и нормировать с
помощью операции
можно центрировать и нормировать с
помощью операции

Теорема 8
(Центральная предельная теорема для
случая одинаково распределенных
слагаемых).
Пусть случайные величины
![]() взаимно
независимы, одинаково распределены,
имеют конечные математическое ожидание
взаимно
независимы, одинаково распределены,
имеют конечные математическое ожидание
![]() и дисперсию
и дисперсию
![]() ,
,
![]() .
Тогда функция распределения центрированной
и нормированной суммы этих случайных
величин стремится при
.
Тогда функция распределения центрированной
и нормированной суммы этих случайных
величин стремится при
![]() к функции распределения стандартной
нормальной случайной величины:
к функции распределения стандартной
нормальной случайной величины:
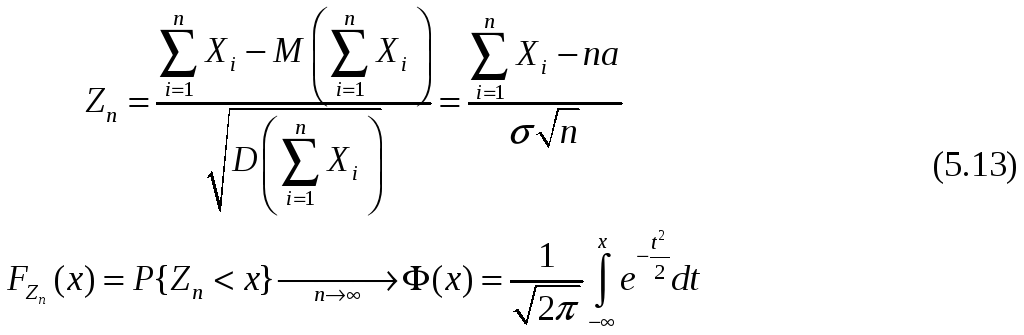
Из отношения (5.13)
следует, что при достаточно большом n
сумма
![]() приближенно распределена по нормальному
закону:
приближенно распределена по нормальному
закону:
![]() ~
~![]() .
Это означает, что сумма
.
Это означает, что сумма
![]() приближенно распределена по нормальному
закону:
приближенно распределена по нормальному
закону:
![]() ~
~![]() .
Говорят, что при
.
Говорят, что при
![]() случайная величина
случайная величина
![]() асимптотически
нормальна.
асимптотически
нормальна.
Примеры:
-
Ошибка измерения распределена нормально, так как является суммой большого числа малых ошибок, проистекающих из колебаний параметров среды (температура, влажность, давление и т.д.), колебаний измерительного инструмента, состояния измеряющего субъекта и т.д.
-
По аналогичным причинам распределены нормально координаты точки падения снаряда.
-
Нормально распределена шумовая помеха в управляющем устройстве.
Формула (5.13) позволяет при больших n вычислять вероятности различных событий, связанных с суммами случайных величин. С её помощью можно получить формулу для определения вероятности того, что сумма нескольких случайных величин окажется в заданных пределах:
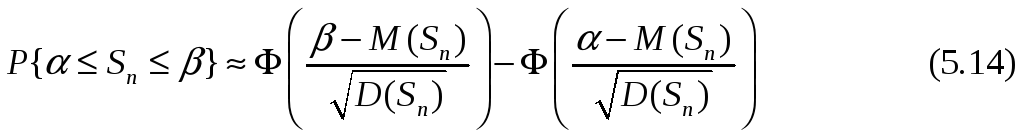
Пример 67.
Независимые случайные величины
![]() распределены равномерно на отрезке [0,
1]. Найти закон распределения случайной
величины
распределены равномерно на отрезке [0,
1]. Найти закон распределения случайной
величины
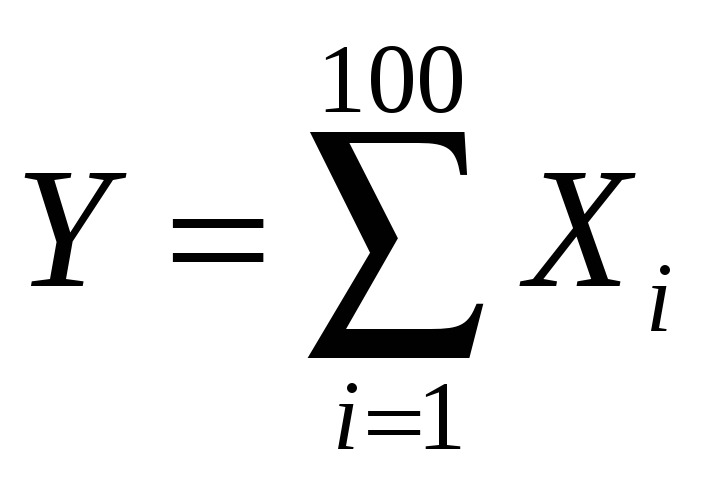 ,
а так же вероятность того, что
,
а так же вероятность того, что
![]() .
.
Решение:
Условия центральной предельно теоремы
наблюдаются, поэтому случайная величина
Y
имеет приближенно плотность распределения
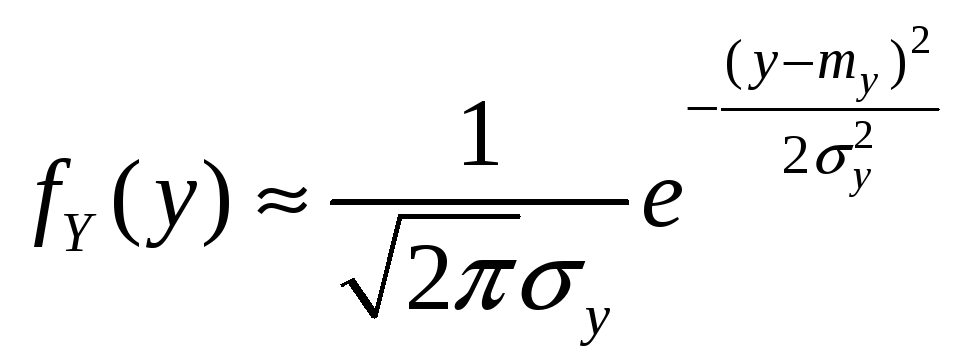 .
Найдем математическое ожидание и
дисперсию в случае равномерного
распределения по формулам (3.37):
.
Найдем математическое ожидание и
дисперсию в случае равномерного
распределения по формулам (3.37):
![]() ,
,
![]() ,
,
![]() .
Тогда
.
Тогда
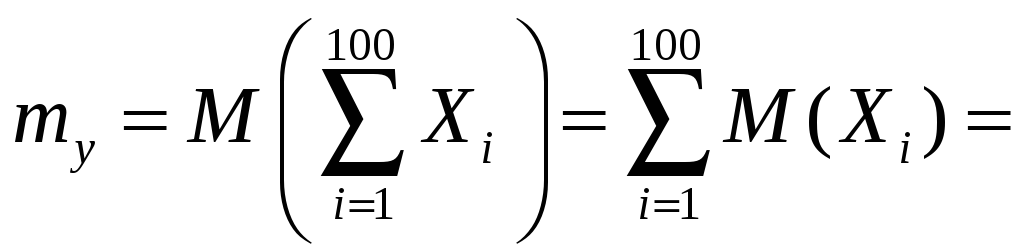
![]() ,
,
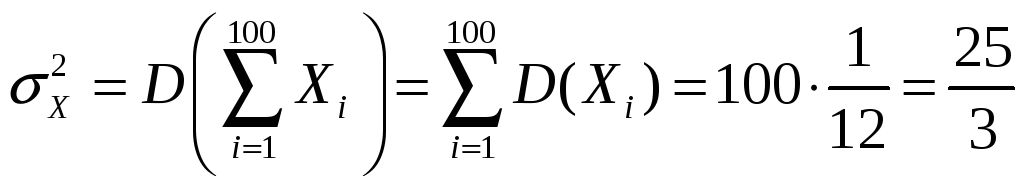 ,
,
![]() .
Поэтому
.
Поэтому
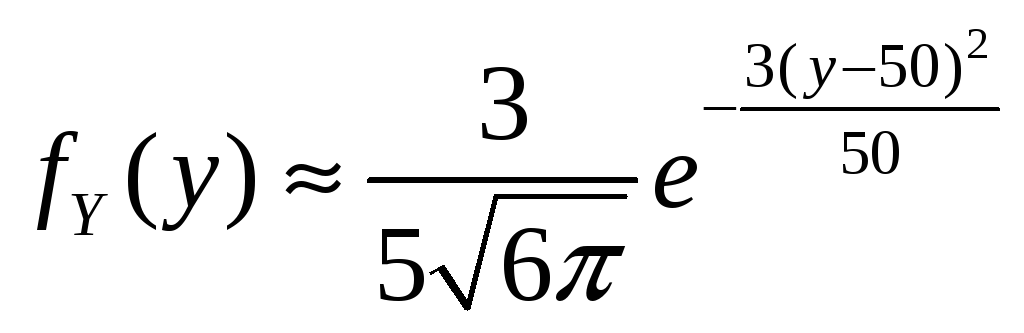 .
Используя формулу (5.14) находим
.
Используя формулу (5.14) находим
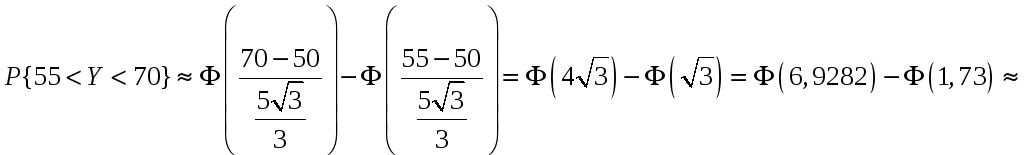
![]() .
.
§35. Интегральная теорема Муавра - Лапласа.
Пусть
![]() - число появлений события A
в n
независимых испытаниях по схеме Бернулли,
в каждом из которых событие A
появляется с вероятностью
- число появлений события A
в n
независимых испытаниях по схеме Бернулли,
в каждом из которых событие A
появляется с вероятностью
![]() .
Тогда для любых a
и b,
.
Тогда для любых a
и b,
![]() ,
имеет место предельное соотношение
,
имеет место предельное соотношение
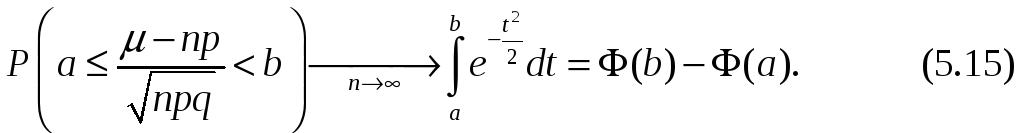
Функция
![]() – функция Лапласа (3.43).
– функция Лапласа (3.43).
Интегральная теорема Муавра – Лапласа является следствием центральной предельной теоремы, хотя была доказана ранее независимо.
На ней основана интегральная приближенная формула Муавра – Лапласа, применяемая для подсчета сумм биноминальных вероятностей:
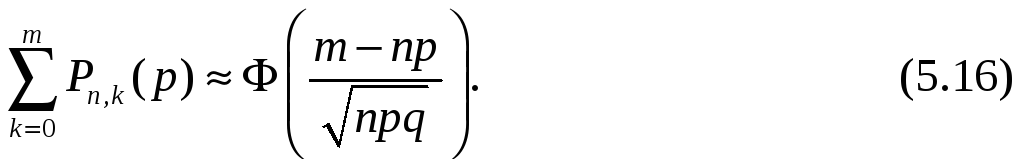
Что вытекает из
формул (2.21) и (3.44):
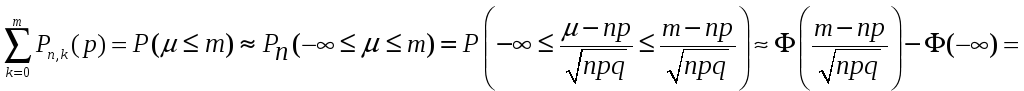
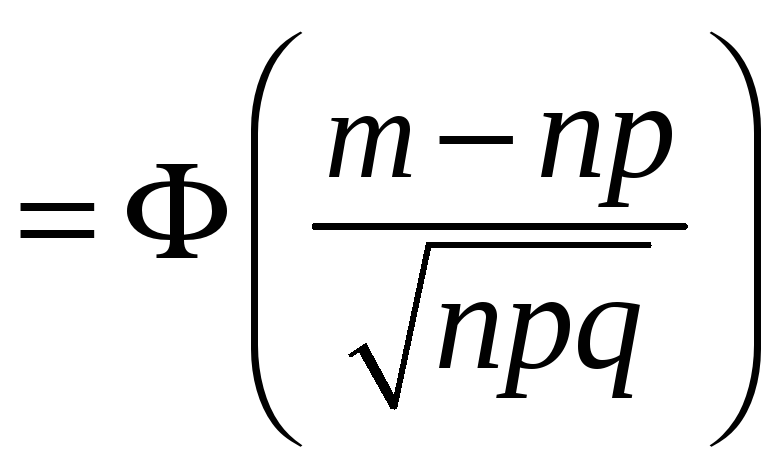 .
.
Формула (5.16)
применяется при больших n
и малых p,
таких, чтобы число
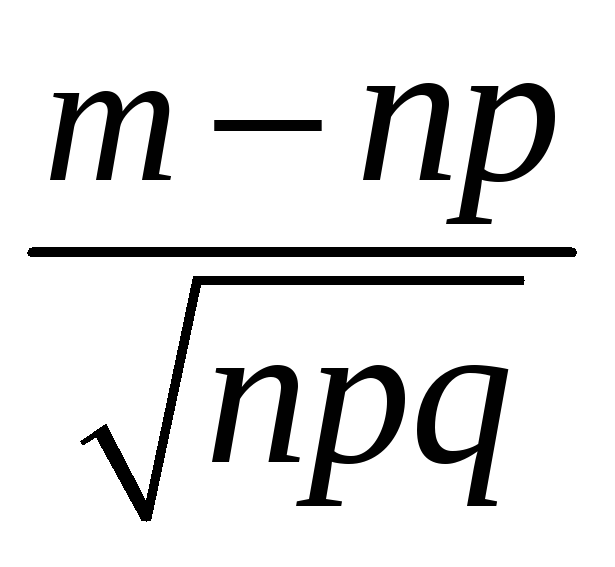 было средним – в пределах таблицы
значений аргумента для функции Лапласа,
то есть в пределах от 0 до 5.
было средним – в пределах таблицы
значений аргумента для функции Лапласа,
то есть в пределах от 0 до 5.
Пример 68.
По каналу связи передано
![]() символов. Вероятность искажения каждого
символа помехами
символов. Вероятность искажения каждого
символа помехами
![]() .
Действие помех на каждый символ происходит
независимо. Какова вероятность, что при
передаче будет не более 15 искажений?
.
Действие помех на каждый символ происходит
независимо. Какова вероятность, что при
передаче будет не более 15 искажений?
Решение:
Так как
![]() ,
то
,
то
![]() .
Применяем
формулу (5.16):
.
Применяем
формулу (5.16):
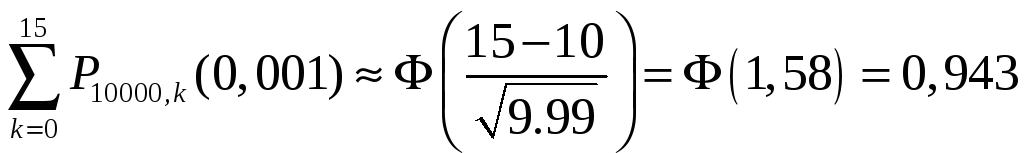 .
.
