Порядок выполнения работы

• Соберите цепь согласно схеме (рис. 6.1.4), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 5 В, f = 1 кГц.

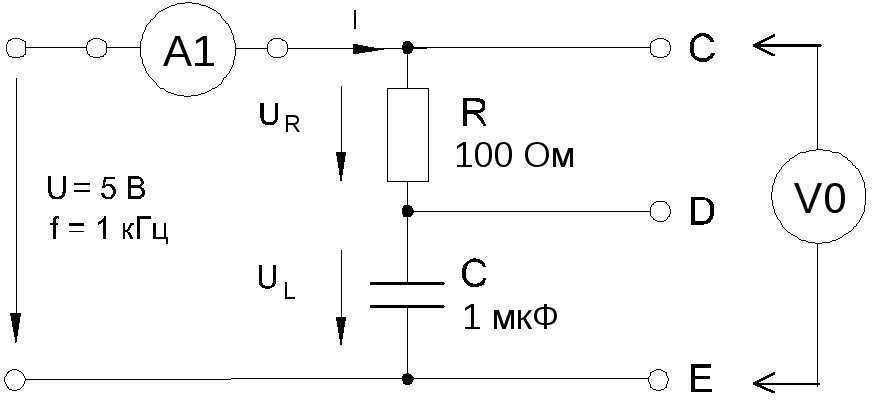
Рис. 6.1.4

• Выполните мультиметрами или виртуальными приборами измерения действующих значений тока и напряжений, указанных в табл. 6.1.1. При измерениях напряжений подключайте мультиметр или канал V0 коннектора к зажимам C-E, C-D, D-E:

Таблица 6.1.1.

U, B	UR, B	UC, B	I, мА	, град	R, Ом	XC, Ом	Z, Ом	Примечание
								Расчет
								Вирт. Изм

• Вычислите:

Фазовый угол

 = arctg (U_C  U_R) =

Полное сопротивление цепи

Z = U  I =

Активное сопротивление цепи

R = Z cos 

Емкостное реактивное сопротивление цепи

X_C = Z sin 

• Если вы работаете с виртуальными приборами, то измерьте с помощью блока «Приборы II» R, , X_C, Z и запишите их значения также в таблицу 6.1.1 под рассчитанными величинами. Сравните результаты.

• Выберите масштабы и постройте векторную диаграмму напряжений (рис. 6.1.5) и треугольник сопротивлений (рис. 6.1.6).

Рис. 6.1.5 Рис. 6.1.6

6.2. Параллельное соединение резистора и конденсатора

6.2.1. Общие сведения

Когда к цепи (рис. 6.2.1) с параллельным соединением резистора и конденсатора подается переменное синусоидальное напряжение, одно и то же напряжение приложено к обоим компонентам цепи.

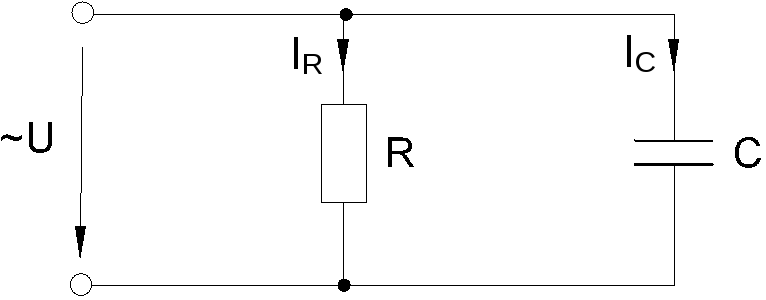
Рис. 6.2.1

Общий ток цепи I разветвляется на ток в конденсаторе I_C (емкостная составляющая общего тока) и ток в резисторе I_R (активная составляющая).

Между токами I, I_C и I_R существуют фазовые сдвиги, обусловленные емкостным реактивным сопротивлением X_C конденсатора. Они могут быть представлены с помощью векторной диаграммы токов (рис. 6.2.2).

Рис. 6.2.2	Рис. 6.2.3

Фазовый сдвиг между напряжением U цепи и током в резисторе I_R отсутствует, тогда как между этим напряжением и током в конденсаторе I_C равен –90⁰ (т.е. ток опережает напряжение на 90⁰). При этом сдвиг между полным током I и напряжением U цепи определяется соотношением между проводимостями B_C и G. Разделив каждую сторону треугольника токов на напряжение, получим треугольник проводимостей (рис. 6.2.3).

В треугольнике проводимостей G=1/R, B_C=1/X_C, а Y представляет собой так называемую полную проводимость цепи в См, тогда как G – активная, а B_C – реактивная (емкостная) проводимости.

Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение действующих или амплитудных токов в параллельных ветвях невозможно. Но в векторной форме:I = I_R +I_C.

Расчет ведется по следующим формулам, вытекающим из векторной диаграммы и треугольника проводимости:

Действующее значение полного тока цепи

; I = U  Z = UY.

Полная проводимость цепи

; Y = I U = 1/Z ,

где Z - полное сопротивление цепи.

Угол сдвига фаз

 = arctg (I _C  I_R) = arctg (B_C  G).

Активная и реактивная проводимости

G = Y cos; B_C = Y sin.