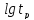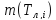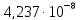- •6 Расчет температур и напряжения в критической точке лопатки на всех режимах опц
- •7 Расчет повреждаемости лопатки на длительной прочности (дп) за один обобщенный полетный цикл (опц)
- •8 Расчет повреждаемости лопатки по мцу за один опц
- •9 Оценки ресурсов лопатки по дп и мцу
- •Заключение
- •Перечень ссылок
6 Расчет температур и напряжения в критической точке лопатки на всех режимах опц
Постановка задачи – необходимо рассчитать температуры и напряжения в критической точке лопатки на всех режимах ОПЦ. Упрощенный ОПЦ двигателя Д-336 приведен на рисунке 1.
Получить
приближенные оценки значений
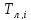 и
и
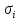 на различных режимах ОПЦ по следующим
формулам:
на различных режимах ОПЦ по следующим
формулам:


 –
напряжение
в критической точке лопатки на базовом
режиме ОПЦ,
–
напряжение
в критической точке лопатки на базовом
режиме ОПЦ,
 –
величина
средней интенсивности оборотов на i-ом
режиме ОПЦ,
–
величина
средней интенсивности оборотов на i-ом
режиме ОПЦ,
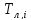 –
температура
в критической точке лопатки на i-ом
режиме ОПЦ,
–
температура
в критической точке лопатки на i-ом
режиме ОПЦ,
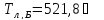 – температура
в критической точке лопатки на базовом
режиме.
– температура
в критической точке лопатки на базовом
режиме.
Полученные
величины упругих напряжений
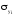 сравниваем со справочными данными по
пределам текучести материала
сравниваем со справочными данными по
пределам текучести материала
 для
соответствующих температур Тi
с целью выявления особых
режимов ОПЦ,
на которых возникают пластические
деформации .
для
соответствующих температур Тi
с целью выявления особых
режимов ОПЦ,
на которых возникают пластические
деформации .
Таблица 3 - Результаты расчетов температур Тi и упругих σуi на режимах ОПЦ
|
№ |
режимы |
|
|
|
|
|
|
|
Приме чание |
|
|
1 |
Малый газ |
0.55 |
8140 |
0,0834 |
421,7 |
92,6 |
166,7 |
680 |
|
|
|
2 |
Взлетный |
1.1 |
16280 |
0,0834 |
843,5 |
370,6 |
667 |
560 |
Особый режим |
605 |
|
3 |
Номинальный |
1 |
14800 |
0,567 |
766,8 |
306,3 |
551 |
570 |
|
|
|
4 |
Полетный МГ |
0,7 |
10360 |
0,0333 |
536,7 |
150 |
270 |
610 |
|
|
Отметим, что режим малый газ практически не влияет на ресурс лопатки, поэтому он исключается из расчета повреждаемости лопатки по критерию длительной прочности.
Определение
упруго-пластических напряжений
 на особых режимах ОПЦ, на которых они
возникают
на особых режимах ОПЦ, на которых они
возникают
Для особых режимов ОПЦ по справочным
данным строим диаграммы "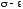 "
материала лопатки для соответствующих
режиму ее температур.
"
материала лопатки для соответствующих
режиму ее температур.
Далее, исходя из соответствующих
особым режимам значениям
 проводим
гиперболу Нейбера в соответствии с
формулой
проводим
гиперболу Нейбера в соответствии с
формулой
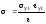
до пересечения с кривой " ".
Точка этого пересечения с координатами
σi и εi, соответствует
искомому НДС критической точки лопатки
с учетом пластических деформаций.
".
Точка этого пересечения с координатами
σi и εi, соответствует
искомому НДС критической точки лопатки
с учетом пластических деформаций.
Гипербола
Нейбера начинается из точки пересечения
горизонтальной прямой
 и продолжения линейного участка диаграммы
"
и продолжения линейного участка диаграммы
"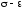 ».
».

Рис.6 – Определение упруго-пластических деформаций
7 Расчет повреждаемости лопатки на длительной прочности (дп) за один обобщенный полетный цикл (опц)
7.1
Необходимо определить время
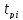 до разрушения материала лопатки на i-х
установившихся режимах ОПЦ.
до разрушения материала лопатки на i-х
установившихся режимах ОПЦ.
Первый
способ заключается в построении на
основе модели Ларсена-Миллера более
простой модели «Кривые длительной
прочности» для всех i
температур
 .
Для этого необходимо:
.
Для этого необходимо:
-
Задаться значениями времени до разрушения
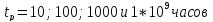 .
По формуле
.
По формуле
 определить значение параметров
Ларсена-Миллера
определить значение параметров
Ларсена-Миллера
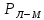 для указанных
для указанных
 .
. -
Подставить значения
 в уравнение модели Ларсена-Миллера и
найти значение
в уравнение модели Ларсена-Миллера и
найти значение
 .
Кривая Ларсона-Миллера приведена на
рисунке 6.
.
Кривая Ларсона-Миллера приведена на
рисунке 6.
Результаты вычислений заносим в таблицу 4.
Таблица
4 - Результаты построения кривых ДП
материала лопатки для температур
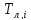 на взлетном, номинальном и крейсерском
режимах ОПЦ.
на взлетном, номинальном и крейсерском
режимах ОПЦ.
|
Режимы |
Максимальный |
Максимально продолжительный |
|||||||||||
|
Время
до разрушения
|
10 |
100 |
1000 |
10000 |
… |
10000000 |
10 |
100 |
1000 |
10000 |
… |
1000000000 |
|
|
|
1 |
2 |
3 |
4 |
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
17787 |
18634 |
19481 |
20328 |
|
22869 |
16690,8 |
17485,6 |
18280,4 |
19075,2 |
|
23049 |
|
|
|
2.938 |
2.933 |
2.923 |
2.907 |
|
2,82 |
2.9399 |
2.9395 |
2.9359 |
2.9284 |
|
2,811 |
|
|
|
50,657 |
62,216 |
|||||||||||
Полученные таким образом кривые ДП материала лопатки для указанных режимов поместим на рисунке 7.

Рисунок 7 – Кривые ДП материала лопатки турбины для i-го режима ОПЦ
-
По кривым длительной прочности для соответствующих температур
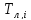 и значениям
и значениям
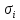 найти время до разрушения
найти время до разрушения
 .
.
Если
кривая ДП для режима имеет возрастающий
характер, но с возрастанием напряжения
время до разрушения должно убывать,
тогда
 на этом режиме определяем вторым
способом.
на этом режиме определяем вторым
способом.
Второй
способ заключается в крупномасштабном
построении зависимости
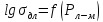 по уравнению Ларсена-Миллера. Задаваясь
значениями
по уравнению Ларсена-Миллера. Задаваясь
значениями
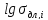 из построенной кривой Ларсена-Миллера
определяются
из построенной кривой Ларсена-Миллера
определяются
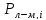 и далее, исходя из формулы
и далее, исходя из формулы
 ,
значения
,
значения
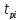 .
.
7.2.
Определить повреждаемости лопатки по
ДП на каждом режиме и суммарную
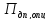 за один ОПЦ по формуле:
за один ОПЦ по формуле:
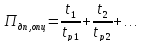

Результаты расчетов заносим в таблицу 5.
Таблица 5 - Расчет повреждений лопатки ПДП, ОПЦ по ДП по отдельным режимам и в целом по ОПЦ.
|
Номер режима |
Обозначение режима |
Время работы ti на i-ом режиме |
Время tpi до разрушения |
Повреждение на i-м режиме |
|
1 |
Максимальный |
6 мин. |
0,055*108
|
|
|
2 |
Максимально продолжительный |
1800 мин. |
7,08*108
|
|
ПДП,
ОПΣ=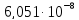
7.3.
Находим параметр
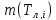 из известной модели ДП.
из известной модели ДП.
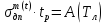
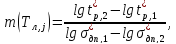
где
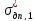 и
и
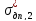 - значения напряжений для заданных
значений
- значения напряжений для заданных
значений
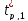 и
и
 .
Рекомендуется задавать
.
Рекомендуется задавать
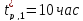 и
и
 .
.


 ,
1/мин
,
1/мин ,
часы
,
часы ,
,
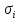 ,
МПа
,
МПа МПа
МПа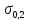 ,
МПа
,
МПа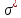 ,
МПа
,
МПа