3. Напряженное и деформированное состояния упругого тела. Связь между напряжениями и деформациями
3.1. Понятие о напряжении тела в данной точке. Нормальные и касательные напряжения
Внутренние силовые факторы, возникающие при нагружении упругого тела, характеризуют состояние того или иного сечения тела, но не дают ответа на вопрос о том, какая именно точка поперечного сечения является наиболее нагруженной, или, как говорят, опасной точкой. Поэтому необходимо ввести в рассмотрение какую-то дополнительную величину, характеризующую состояние тела в данной точке.
Если
тело, к которому приложены внешние силы,
находится в равновесии, то в любом его
сечении возникают внутренние силы
сопротивления. Обозначим через
внутреннее усилие, действующее на
элементарную площадку
,
а нормаль к этой площадке через
тогда величина
|
|
(3.1) |
называется полным напряжением.
В
общем случае полное напряжение не
совпадает по направлению с нормалью к
элементарной площадке, поэтому удобнее
оперировать его составляющими вдоль
координатных осей —
Если
внешняя нормаль совпадает с какой-либо
координатной осью, например, с осью Х,
то составляющие напряжения примут вид
при этом составляющая
оказывается перпендикулярной сечению
и называется нормальным
напряжением,
а составляющие
будут лежать в плоскости сечения и
называются касательными
напряжениями.
Чтобы
легко различать нормальные и касательные
напряжения обычно применяют другие
обозначения:
— нормальное напряжение,
— касательное.
Выделим
из тела, находящегося под действием
внешних сил, бесконечно малый
параллелепипед, грани которого параллельны
координатным плоскостям, а ребра имеют
длину
.
На каждой грани такого элементарного
параллелепипеда действуют по три
составляющие напряжения, параллельные
координатным осям. Всего на шести гранях
получим 18 составляющих напряжений.
Нормальные
напряжения обозначаются в виде
,
где индекс
обозначает нормаль к соответствующей
грани (т.е. может принимать значения
).
Касательные напряжения имеют вид
;
здесь первый индекс соответствует
нормали к той площадке, на которой
действует данное касательное напряжение,
а второй указывает ось, параллельно
которой это напряжение направлено
(рис.3.1).
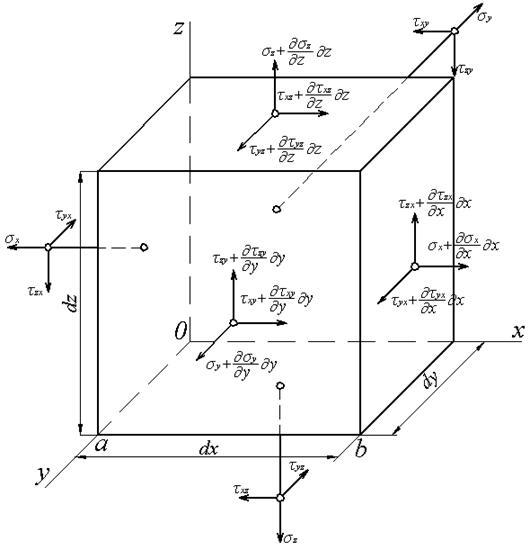
Рис.3.1. Нормальные и касательные напряжения
Для этих напряжений принято следующее правило знаков. Нормальное напряжение считается положительным при растяжении, или, что то же самое, когда оно совпадает с направлением внешней нормали к площадке, на которой действует. Касательное напряжение считается положительным, если на площадке, нормаль к которой совпадает с направлением параллельной ей координатной оси, оно направлено в сторону соответствующей этому напряжению положительной координатной оси.
Составляющие
напряжений являются функциями трех
координат. Например, нормальное напряжение
в точке с координатами
можно обозначать
В
точке, которая отстоит от рассматриваемой
на бесконечно малом расстоянии, напряжение
с точностью до бесконечно малых первого
порядка можно разложить в ряд Тейлора:
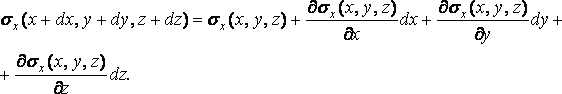
Для
площадок, которые параллельны плоскости
изменяется только координата х,
а приращения
Поэтому
на грани параллелепипеда, совпадающей
с плоскостью
нормальное напряжение будет
,
а на параллельной грани, отстоящей на
бесконечно малом расстоянии
,
—
Напряжения на остальных параллельных
гранях параллелепипеда связаны
аналогичным образом. Следовательно, из
18 составляющих напряжения неизвестными
являются только девять.
В теории упругости доказывается закон парности касательных напряжений, согласно которому по двум взаимно перпендикулярным площадкам составляющие касательных напряжений, перпендикулярные линии пересечения этих площадок, равны друг другу:
|
|
(3.2) |
Равенства (3.2) приводят к тому, что из девяти составляющих напряжений, характеризующих напряженное состояние в точке тела, остаются только шесть:
|
|
(3.3) |
Можно показать, что напряжения (3.3) не просто характеризуют напряженное состояние тела в данной точке, но определяют его однозначно. Совокупность этих напряжений образует симметричную матрицу, которая называется тензором напряжений:
|
|
(3.4) |
Так как в каждой точке будет свой тензор напряжений, то в теле имеется поле тензоров напряжений.
Тензоры можно складывать и вычитать, при этом суммой двух тензоров является тензор, компоненты которого представляют собой сумму соответствующих компонентов слагаемых тензоров.
При
умножении тензора на скалярную величину
получится новый тензор, все компоненты
которого в
раз больше компонентов исходного
тензора.
НА ОГЛАВЛЕНИЕ ДАЛЕЕ