20). Сходимость и частичные пределы.

Сходимость и ограниченность ТЕОРЕМА {x _n } - сходится ⇒ сходится любая её подпоследоватедьность, причём к тому же числу ДОК-ВО: Пусть x _n → A при n → ∞ т.е. ∀ n > N ⇒ |x _n - A| > ε  Пусть k > N ⇒ n _k ≥ k > N ⇒ |x _n - A| < ε  x _n k → A при k → ∞  Ч.Т.Д. СЛЕДСТВИЕ:

У сходящейся последовательности ровно один частичный предел.

ЗАМЕЧАНИЕ: (критерий сходимости)

Если любые подпоследовательности сходятся, то и сама последовательность сходится.

ДОК-ВО:

Очевидно, т.к. x_n своя подпоследовательность.

Определения

1)Аксиома полноты

Полнота R : для любых непустых множеств, таких, что все элементы одного не превышают элементы другого, существует число, разделяющие эти множества.

2)Принцип верхней грани

Непустое ограниченное сверху множество имеет верхнюю грань. Верхняя грань единственна.

ЗАМ : верхняя грань – наименьшая верхняя граница.

3)Принцип предельной точки

Для любого бесконечного ограниченного множества Е существует хотя бы одна предельная точка.

4)Принцип конечного покрытия

Из всякого покрытия отрезка интервалами можно выделить конечное подпокрытие.

5)Принцип вложенных отрезков

Пусть {I_n} – последовательность вложенных отрезков

1). Тогда все эти отрезки имеют общую точку, т.е. , что

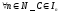
2). Если в этой последовательности {I_n}есть отрезки сколь угодно малой длинны, то такая точка единственна.

6)a – предельная точка

Точка называется предельной точкой для если в любой её окрестности содержится бесконечно много точек из Е (Для конечных множеств)

7)

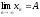
8) {a_n} – фундаментальна

ОПРЕДЕЛЕНИЕ

Последовательность называется фундаментальной если

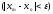
9)Критерий Коши

Числовая последовательностьсходится тогда и только тогда, когда она фундаментальна

10)Критерий монотонной сходимости

Пусть монотонна, тогда она сходится она ограничена.

Для заметок

29