Задачи на теоремы сложения и умножения вероятностей

Задача 1: Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,95, во второе - 0,9, в третье - 0,8. Найти вероятность следующих событий: а) только одно отделение получит газеты вовремя; б) хотя бы одно отделение получит газеты с опозданием.

Решение: Введем события А1 = (газеты доставлены своевременно в первое отделение), А2 = (газеты доставлены своевременно во второе отделение), А3 = (газеты доставлены своевременно в третье отделение), по условию P(A1)=0,95; P(A2) = 0,9; P(A3)=0,8. Найдем вероятность события Х = (только одно отделение получит газеты вовремя). Событие Х произойдет, если или газеты доставлены своевременно в 1 отделение, и доставлены не вовремя во 2 и 3, или газеты доставлены своевременно в 2 отделение, и доставлены не вовремя во 1 и 3, или газеты доставлены своевременно в 3 отделение, и доставлены не вовремя во 2 и 1. 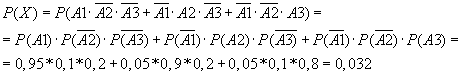Таким образом, Так как события А1, А2, А3 - независимые, по теоремам сложения и умножения получаем Найдем вероятность события У=(хотя бы одно отделение получит газеты с опозданием). Введем противоположное событие =(все отделения получат газеты вовремя). Вероятность этого события Тогда вероятность события У: Ответ: 0,032; 0,316.

Задача 2: Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго.Найти вероятность того, что при аварии сработает только один сигнализатор.

Решение:Введем независимые события: А1 = (при аварии сработает первый сигнализатор); А2 = (при аварии сработает второй сигнализатор); по условию задачи P(A1)=0,95, P(A2)=0,9. Введем событие Х = (при аварии сработает только один сигнализатор). Это событие произойдет, если при аварии сработает первый сигнализатор и не сработает второй, или если при аварии сработает второй сигнализатор и не сработает первый, то есть Тогда вероятность события Х по теоремам сложения и умножения вероятностей равна Ответ: 0,14.

Задача 3: Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.

Решение:Пусть - вероятность попадания в цель при одном выстреле. Введем событие X = {при четырех выстрелах есть хотя бы одно попадание} и противоположное ему событие = {при четырех выстрелах нет ни одного попадания}. Вероятность события равна,тогда вероятность события Х равна . По условию эта вероятность равна 0,9984, откуда получаем уравнение относительно Ответ: 0,8.

Задачи на теоремы Лапласа (Муавра-Лапласа)

Задача 1: В жилом доме имеется n ламп, вероятность включения каждой из них в вечернее время равна 0,5. Найти вероятность того, что число одновременно включенных ламп будет между m1 и m2.Найти наивероятнейшее число включенных ламп среди n и его соответствующую вероятность. n = 6400, m1 = 3120, m2 = 3200.

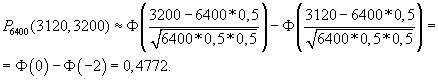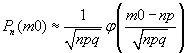
Решение: Используем интегральную теорему Лапласа: , где n = 6400, p = 0.5, q = 1-p = 0.5, m1 =3120, m2 = 3200, Ф - функция Лапласа (значения берутся из таблиц). Подставляем: Найдем наивероятнейшее число включенных ламп среди n из неравенства: Отсюда m0=3200. Найдем вероятность по локальной теореме Лапласа: Ответ: 0,4772; 3200; 0,0099752..

Задача 2: Вычислительное устройство состоит из 1000 элементов, работающих независимо друг от друга. Вероятность отказа каждого элемента за смену равна р. Найти вероятность, что за смену откажут m элементов. р= 0,024, m=6.

Решение: Используем локальную теорему Лапласа: 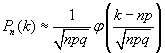. Здесь n=1000, k =6, p=0,024, q= 1-p = 0,976, значения функции берутся из таблицы. Подставляем: Ответ: 0,000084

Задача 3: Найти вероятность того, что если бросить монету 200 раз, то орел выпадет от 90 до 110 раз.

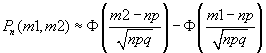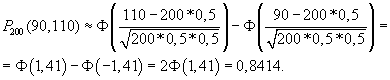Решение: Имеем схему Бернулли с параметрами n = 200, p = q = 1/2 (вероятность выпадения орла/решки). Так как число n достаточно велико, будем использовать интегральную теорему Лапласа для подсчета вероятности: , где m1 =90, m2 = 110, Ф - функция Лапласа (значения берутся из таблиц). Подставляем: Ответ: 0,8414.