Электромагнитные колебания
-
Уравнение собственных колебаний
-
контура:
,
где
- циклическая частота собственных
колебаний; период колебаний
. -
Уравнение затухающих колебаний в
- контуре:
,
где
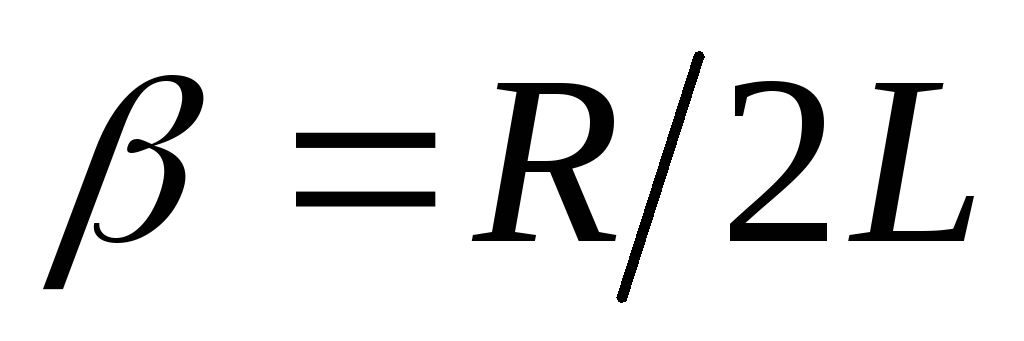- коэффициент затухания. Затухающие
колебания происходят по закону:
,
где
-
циклическая частота; постоянные
и
определяются начальными условиями.
Колебания возможны при условии, что
<
.
-
Амплитуда затухающих колебаний
. -
Логарифмический декремент затухания
=
,
где Т – период; при слабом затухании
(
<<
)
.
-
Добротность контура
;
при слабом затухании
.
Электромагнитные волны
-
Уравнения Максвелла в интегральной форме:
,
,
,
,
где
- объемная плотность сторонних зарядов,
- плотность тока проводимости.
-
Уравнения Максвелла в дифференциальной форме:
,
,
,
.
-
Плотность тока смещения
;
плотность полного тока
.
4. Инварианты электромагнитного поля:
,
-
Фазовая скорость электромагнитных волн
,
где
- фазовая скорость в вакууме.
-
Объемная плотность энергии в электромагнитной волне
,
причем в бегущей электромагнитной волне оба слагаемых равны.
-
Связь Е и Н в бегущей электромагнитной волне:
,
где
Ом – волновое сопротивление вакуума.
Связь Е и В в бегущей электромагнитной волне:
( в вакууме
).
-
Для электромагнитных волн, распространяющихся вдоль проводов, напряжение между проводами и сила тока в них связаны соотношением:
,
где
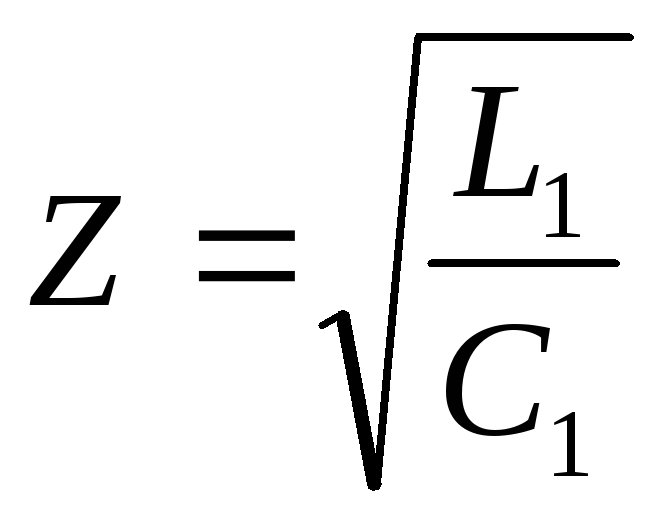- волновое сопротивление линии (
и
- соответственно индуктивность и емкость
на единицу длины линии). -
Плотность потока энергии в волне (вектор Умова-Пойнтинга)
.
10. Интенсивность волны
равна средней (по времени) плотности
потока энергии. Связь интенсивности со
средней плотностью энергии
и с амплитудой напряженности
в волне:
.
В вакууме
.
1 Подробнее о правилах знаков см. решение задачи 5.35.
2
Строго говоря, в этой формуле zе –
заряд того сорта ионов, концентрация
которых равна концентрации
диссоциировавших молекул. Например,
при диссоциации
концентрация отрицательных ионов
,
а для положительных
.
Но в силу электронейтральности раствора
и для сокращения вводят обозначение
.