Вопрос 2. Математическая основа построения топографичес-ких карт.

Понятия: уровенная поверхность, геоид, земной эллипсоид, эллипсоид Крассовского, сфероид, географический полюс, экватор, плоскость земного экватора, земное полушарие, параллели, географические (истинные) меридианы, географическая сетка, картографическая сетка, горизонтальное проложение, картографическая проекция, равномасштабность изображения, свойство равноугольности, равновеликость изображения, равноугольная проекция, равноплощадная проекция, равновеликая проекция, произвольная проекция.

Для изображения земной поверхности на топографических планах и картах рассмотрим во­прос о форме и размерах Земли и основные правила получения такого изображения. Чтобы правильно и полноценно использовать карты в качестве измерительных документов, необходимо хорошо уяснить их геометрическую сущность и математические принципы их построения.

Форма и размеры Земли.

Геометрия картографического изображения связана с представлением о фигуре Земли – ее геометрической форме и размерах. Планета Земля не имеет правильной геометрической формы.

Когда говорят о форме (фигуре) Земли, то имеют в виду не физическую ее поверхность со всеми неровностями (горами, низменностями и т.п.), а некоторую воображаемую поверхность океанов и открытых морей. Под фигурой Земли понимают математическую фигуру, ограниченную поверхностью среднего уровня Мирового океана в спокойном его состоянии, мысленно продолженную под всеми континентами. Эта воображаемая поверхность, перпендикулярная в любой ее точке к направлению отвесной линии (направлению силы тяжести), называется основной уровенной поверхностью, а фигура Земли, образованная ею, – геоидом.

Рис. 1. Физическая и математическая поверхность Земли.

Принято считать, что по форме Земля близка к эллипсоиду, получающемуся при вращении эллипса вокруг малой оси. Единых, общепринятых во всех странах размеров земного эл­липсоида до сего времени не установлено. В Российской Федерации и в других европейских странах за основу при создании топографических карт и определении координат геодезических пунктов принят эллипсоид Красовского.

Выдающийся русский ученый-геодезист Феодосий Николаевич Красовский в 1940 – 1942 годах руководил научной обработкой огромного материала измерений. В результате были получены но­вейшие, более точные данные о разме­рах земного эллипсоида.

На данных эллипсоида Крассовского была основана геодезическая система координат «Пулково-1942» (СК-42). СК-42 по постановлению Совета Министров № 760 введена с 1946 года для выполнения работ на всей территории СССР. Она же взята за основу в СК-63, используемой в нашей и некоторых других странах, а также систем координат Afgooye и Hanoi 1972.

С 1 июля 2002 года согласно Постановлению Правительства Российской Федерации от 28 июля 2000 года № 568 введена новая система СК-95, также основанная на эллипсоиде Красовского.

Рис. 2. Крассовский Феодосий Рис. 3. Эллипсоид Крассовского

Николаевич (1878 – 1948)

Размеры земного эллипсоида по Крассовскому Таблица № 1.

Малая полуось (полярный радиус), м	6 356 863
Большая полуось (экваториальный радиус), м	6 378 245
Средний радиус Земли, принимаемой за шар, м	6 371 100
Полярное сжатие (отношение разницы полуосей к большой полуоси)	1 / 298,3
Площадь поверхности Земли, км²	510 083 058
Длина меридиана, км	19 980
Длина экватора, км	40 075,7
Длина дуги 1° по меридиану на широте 0°, км	110,6
Длина дуги 1° по меридиану на широте 45°, км	111,1
Длина дуги 1° по меридиану на широте 60°, км	111,7

Из этих данных видно, что ось вра­щения Земли короче диаметра земно­го экватора примерно на 43 км. По­этому для ряда практических за­дач, не требующих особой точности, фигуру Земли принимают за шар.

Геоид, как показали исследования, имеет всюду выпуклую, но асимметричную, сложную и неправильную в геометрическом отношении фигуру, которая, однако, весьма мало отличается от эллипсоида вращения, т.е. правильного геометрического тела, образуемого вращением эллипса вокруг его малой оси (рис. 4). Отступления по вы­соте точек поверхности геоида от поверхности наиболее близко подходящего к нему по своим размерам эллипсоида характеризуются в среднем величиной порядка 50 м и не превосходят 150 м. Такие расхождения столь незначительны по сравнению с размерами Земли, что на практике ее форму принимают за эллипсоид, кото­рый называют земным эллипсоидом, или сфероидом. Поэтому при геодезических измерениях и составлении карт фигуру Земли и принимают за такой эллипсоид.

Рис. 4. Фигура Земли: геоид и земной эллипсоид (сфероид).

На земном шаре (эллипсоиде) (рис. 5) различают следующие основные точки и линии.

Концы земной оси, вокруг которой происходит суточное вращение Земли, называют географическими полюсами – северным (Р) и южным (Р₁).

Плоскость, перпендикулярная к оси вращения Земли и проходящая через ее центр, называется пло­скостью земного экватора.

Рис. 5. Основные точки и линии на земном шаре.

Эта плоскость пересекает зем­ную поверхность по окружности, называемой экватором (ЕЕ_{). Плоскость экватора делит Землю на два полушария – северное и южное. Линии пересечения земной поверхности плоскостями, па­раллельными плоскости экватора, называются параллелями, а линии пересечения поверхности Земли вертикальными плоско­стями, проходящими через земную ось, – географическими или истинными меридианами.

На рис. 5 параллелью точки М является линия АМА₁ , а мери­дианом – линия РМР₁. Сетка, образованная пересекающимися меридианами и парал­лелями, называется географической сеткой.

Геометрическая сущность картографического изображения.

Географическое положение точек на земной поверхности определяется, как известно, их координатами. Поэтому математическая задача построения картографического изображения заключается в том, чтобы спроектировать и изобразить шарообразную поверхность Земли на плоскости (карте), строго соблюдая при этом однозначное соответствие между координатами точек на земной поверхности и координатами их изображения на карте.

Такое проектирование сопряжено с необходимостью отнесения результатов полевых геодезических измерений при их вычислительной обработке и отображении на картах к определенной, хорошо изученной в геометрическом отношении поверхности, которая наиболее близко подходит по своей форме и размерам к реальной фигуре Земли, но более проста по сравнению с нею.

На картах эту поверхность представляет сетка географических меридианов и параллелей земного эллипсоида. Такая сетка на картах называется картографической сеткой. При составлении карты прежде строят картографическую сетку, а затем, пользуясь ею как канвой, наносят по материалам топографической съемки, аэроснимкам и другим материалам изображение всех объектов, которые должны быть показаны на карте.

Картографические сетки рассчитываются и строятся на картах по определенным математическим формулам, выражающим определенную для данной карты зависимость между географическими координатами точек на поверхности земного эллипсоида и плоскими прямоугольными координатами соответствующих им точек на карте.

Метод проекции участка физической земной поверхности на поверхность земного эллипсоида с помощью прямых, перпендикулярных к эллипсоиду (нормалей) называется горизонтальной проекцией или горизонтальным проложением.

Чтобы представить геометрическую сущность изображения физической поверхности Земли на карте, т.е. на плоскости, ее первоначально проектируют (переносят) отвесными линиями на уровенную по­верхность (рис. 6), т.е. на поверхность земного эллипсоида (для наглядности представим себе его в виде глобуса).

Рис. 6. Проектирование физической поверхности Земли на уровенную поверхность.

Подобным обра­зом могут быть получены гори­зонтальные проложения любых фигур. Представив этот же процесс в плане (рис. 7), мы можем аналогично спроецировать на кривую плоскость земного эллипсоида (на уровенную поверхность) точку А, прямой отрезок АВ, ломанную АBCDE и кривую ABCDEFG.

Рис. 7. Горизонтальные проложения точки и различного вида линий

на поверхность земного эллипсоида.

Затем уже по определенным правилам это изображение развертывают (т.е. пе­реносят с глобуса) на плоскость. При изображении небольшого участка уровенную поверхность можно принять за горизонтальную плоскость и, спроектировав на нее этот участок, получить план (рис. 8).

Рис. 8. Горизонтальные проложения (изображения в плане)

точки, прямой, ломанной и кривой.

Таким образом, если:

- проектируемая линия горизонтальна, ее изображение в плане равно длине самой линии;

- проектируемая линия наклонна, то горизон­тальное проложение всегда короче ее длины и уменьшается с уве­личением угла наклона.

- проектируемая линия вертикальна, то ее горизонтальное проложение – точка.

При съемке местности на карту наносят в заданном масштабе, т.е. с известным уменьшением, горизонтальные проложения всех ее линий и контуров (очертаний площадей), проектируя их на уровенную поверхность Земли, которую в пределах листа карты при­нимают за горизонтальную плоскость.

Следовательно, нанесение на карту изображения земной поверхности представляет собой процесс двойного проектирования. Он включает одновременно:

1) переход от действительных очертаний изображаемых объектов к их горизонтальным проложениям на поверхности земного эллипсоида (рис. 7), и

2) изображение на плоскости, т.е. на карте, этих горизонтальных проложений в заданном масштабе и по определенным для данной карты математическим правилам (рис. 8).

Математически определяемый способ построения на плоскости картографической сетки того или иного вида, на основе которой на карте изображают поверхность Земли, называется картографической проекцией.

Сущность картографических проекций.

Развернуть сфериче­скую поверхность на плоскости без разрывов и складок нельзя. Это значит, что такую поверхность невозможно представить в виде планового изображения на плоскости без искажений, т. е. с пол­ным соблюдением геометрического подобия всех ее очертаний. Оче­видно, что спроектированные на уровенную поверхность очертания материков, островов и других частей Земли могут быть изобра­жены с полным соблюдением подобия лишь на глобусе.

На глобусе географическая сетка, а, следовательно, и все изо­бражение поверхности Земли обладают следующими основными геометрическими свойствами.

1) Любой отрезок линии на поверхности земного шара изобра­жается на глобусе с одинаковым уменьшением, т. е. масштаб изо­бражения остается на глобусе всюду одинаковым. Все меридианы на глобусе равны по длине между собой. Это свойство называется равномасштабностью изображения.

2) Любой горизонтальный угол на земном шаре равен соответ­ствующему ему углу на глобусе, т.е. изображение на глобусе лю­бой фигуры подобно действительным ее очертаниям в натуре. Все меридианы пересекают параллели под прямым углом. Это свой­ство называется свойством равноугольности.

3) Размеры всех площадей, изображаемых на глобусе, пропор­циональны их действительным размерам на земном шаре, т. е. от­ношение площадей на глобусе к соответствующим площадям на земном шаре постоянно. Это свойство называется свойством равновеликости изображения.

Все эти свойства одновременно и полностью сохранить на кар­те невозможно. Построенная на плоскости, т.е. на карте картографическая сетка (меридианы и параллели) бу­дет в той или иной степени искажена. Соответственно исказится каждая клетка географической сетки, а, следовательно, и изобра­жение всех подробностей земной поверхности, так как необходи­мые измерительные данные о них, полученные по материалам то­пографической съемки или по аэроснимкам, наносят на карту при ее составлении по клеткам картографической сетки.

Для составления карт применяются различные проекции. Каждой из них соответствуют вполне определенный вид картографической сетки и вполне определенные искажения. В одних проекциях искажаются размеры площадей и длина линий, но почти не искажаются углы. Такие проекции называются равноугольными. В других, наоборот, наряду с длиной линий искажаются углы, а размеры площадей (но не их форма) передаются без искажений. Такие проекции называются равноплощадными, или равновеликими. В третьих искажаются, но обычно менее, чем в других проекциях, все структурные элементы чертежа. Это так называемые произвольные проекции.

Картографическая проекция, наиболее подходящая по характеру, величине и распределению искажений для той или иной карты, выбирается в зависимости от назначения, содержания карты, а также от размеров, конфигурации и географического положения картографируемой территории.

На рис. 9 показана карта мира (в уменьшенном виде), на ко­торой картографическая сетка сохраняет свойство равноугольности. Иначе говоря, данная карта составлена в одной из равноугольных проекций. Но на этой карте искажены размеры площадей, в чем нетрудно убедиться, если сравнить, например, размеры Гренландии и Африки; на карте они почти равны между собой, а в действительности площадь Гренландии меньше площади Африки примерно в 15 раз.

Рис. 9. Карта мира в равноугольной проекции.

На рис. 10 карта мира составлена в равновеликой проекции, т.е. ее картографическая сетка сохраняет свойство равновеликости. На такой карте сохранена пропорциональность всех площадей, но нарушено свойство равноугольности (подобие фигур). На глобусе все меридианы пересекают параллели под прямым углом; на этой же карте взаимная перпендикулярность меридианов и па­раллелей сохраняется лишь по среднему меридиану.

 

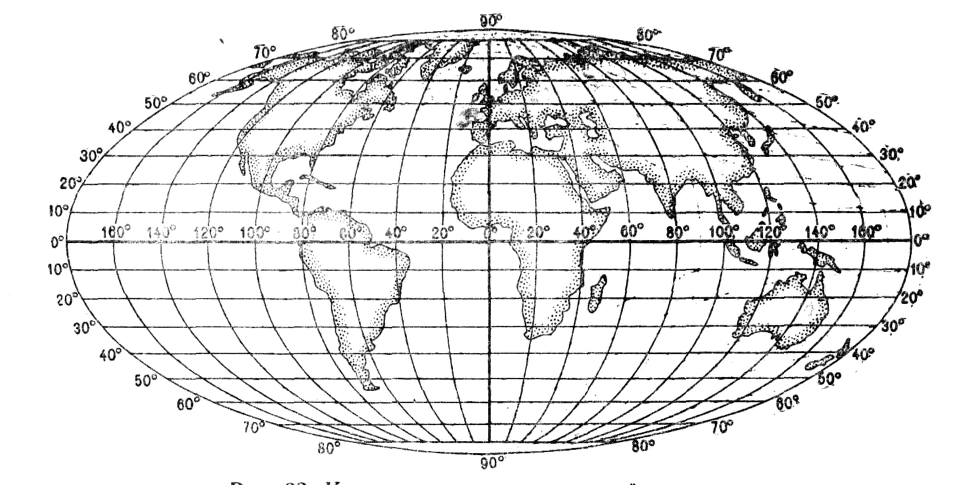
Рис. 10. Карта мира в равномерной плоскости

Таким образом, нельзя построить картографическую сетку, а, следовательно, и карту, на которой бы полностью сохранилось свойство равномасштабности изображения, так как это означало бы одновременное сохранение равноугольности и равновеликости, что может быть достигнуто лишь на глобусе или при изображении сравнительно небольших участков земной поверхности – на плане.

Неизбежные искажения на карте тем значительнее, чем больше изображаемая на ней территория. Поэтому они наиболее сказываются на мелкомасштабных географических картах, изображающих обширные пространства. На крупномасштабных же топографических картах, на которых в пределах каждого листа изображается сравнительно небольшой участок земной поверхности, искажения весьма незначительны и практически не влияют на точность измерений по карте.

Важно подчеркнуть; что, благодаря наличию картографической сетки, все искажения, как бы велики они не были, сами по себе не влияют на точность определения по карте географического положения (координат) изображаемых на ней объектов. Вместе с тем картографическая сетка, являясь графическим выражением проекции, позволяет при измерениях по карте учитывать характер, величину и распределение искажений. В этом смысле любая географическая карта представляет собой точное, математически определенное изображение земной поверхности.

Проекция и масштаб картографического изображения составляют его математическую основу.