
- •Тема 1. Понятийный аппарат теории систем
- •Система - в философском смысле - объективное единство закономерно связанных между собой элементов, предметов, явлений, а также знаний о природе и обществе.
- •Блок обратной связи
- •Тема 2. Сущность и принципы системного подхода,
- •Сущность, элементы и методы системного анализа
- •Метод "Стрелочная диаграмма"
- •Получение максимально возможной прибыли на рынке тур услуг
- •Тема 3. Процесс разработки управленческих решений
- •Тема 4. Метод моделирования – основной метод исследования систем
- •Для начала процедуры сравнения объектов рассматривается гипотеза, что
- •Литература
- •1. Основная:
- •2. Дополнительная:
- •Бизнес-курс. Мва: Системный анализ в менеджменте
- •Глоссарий
- •Структура управления организацией - совокупность специализированных функциональных подразделений, взаимосвязанных в процессе обоснования, выработки, принятия и реализации управленческих решений
-
Для начала процедуры сравнения объектов рассматривается гипотеза, что
еi >еj. Для оценки соответствия различных критериев данной гипотезе вводится показатель соответствия сij
-
Он рассчитывается по формуле:
![]()
(соотв.)
сij=
(всех)
Сумма подтверждений этой гипотезы соответствия к сумме экспертов.
Показатель соотв. рассчитывают для каждой пары объектов еi еj
Для осуществления процедуры сравнения необходимо учесть и критерии, противоречащие введённому предположению, что объект еi по крайней мере не хуже еj . С этой целью рассчитывается показатель не соответствия- сij (s)
-
Для его получения необходимо:
-
Вычислить разности между оценками объектов αik и αjk для всех КDij и упорядочить полученные отклонения (разности) в невозрастающую последовательность.
-
Определить показатель несоответствия как S-ый элемент построенной последовательности.
Пр.: на предприятии проводится отбор платьев для массового пошива, при этом каждое платье оценивают по 6 показателям.
е1 трудоёмкость процесса
е2 удельная прибыль
е3 инвариантность тела ткани
е4 инвариантность фурнитуры
е5 величина охвата рынка
е6 соотв. модной тенденции
Эти показатели получили оценки 10-ти специалистов по 10-ти бальной шкале. Экспертные оценки представлены в таблице:
Таблица «оценки показателей экспертами»
|
показатели |
эксперты |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
е1 |
1 |
9 |
5 |
10 |
7 |
10 |
5 |
5 |
10 |
3 |
|
е2 |
3 |
4 |
5 |
8 |
5 |
3 |
8 |
8 |
5 |
7 |
|
е3 |
8 |
3 |
2 |
5 |
5 |
5 |
8 |
4 |
5 |
2 |
|
е4 |
2 |
6 |
2 |
5 |
10 |
5 |
10 |
9 |
10 |
6 |
|
е5 |
10 |
10 |
4 |
8 |
8 |
10 |
10 |
4 |
10 |
5 |
|
е6 |
9 |
8 |
3 |
7 |
5 |
4 |
10 |
6 |
8 |
7 |
Задача состоит в выборе наиболее значимого элемента еi или группы этих элементов при разных предположениях относительно к требованиям к точности совпадения мнений этих экспертов. Посмотрим матрицу соответствия Сij =
-
е1
е2
е3
е4
е5
е6
е1
х
0,6
0,8
0,5
0,5
0,6
е2
0,5
х
0,8
0,3
0,4
0,5
е3
0,2
0,5
х
0,4
0,1
0,2
е4
0,5
0,4
0,3
х
0,7
0,6
е5
0,5
0,5
0,1
0,5
х
0,8
е6
0,6
0,5
0,9
0,5
0,2
х
Гипотеза: еi >еj
-
е1> е2
e1> е3
e2 >е1
e2 >е3
e2 >е4
e2 >е5
e2 >е6
e2 >е
-
Строим матрицу несоответствия :
Dij =
-
е1
е2
е3
е4
е5
е6
е1
х
0.4
0.7
0.5
0.9
0.8
е2
0.7
х
0.5
0.5
0.7
0.6
е3
0.6
0.5
х
0.5
0.7
0.5
е4
0.5
0.5
0.5
х
0.5
0.7
е5
0.7
0.7
1
0.7
х
0.8
е6
0.6
0.2
0.1
0.5
0.6
х
е1 > е2
[2,3,3,4] = [4.3.3.2]
d12(1) = 0.4
зафиксируем значение параметра S и зададим два числа:
c – пара соответствия
d – пара несоответствия
Будем считать, что согласно введенным критериям и парам c и d, если и только если пара (е1 , е2) приводит к показателю соответствия
сij≥с и dij(s)≤d – показатель несоответствия.
Предпочтения опр. т. обр. удобно представлять в виде графа, вершинами которого являются элементы Е= {еi} множества Е, а дуги выражают отношение предпочтения своим направлением от еi к еj , если еi > еj. Т.е. граф G(c,d,s)=[E,U(c,d,s)] множество Е, которое объединяет дуга. Очевидно, чем меньше требования к значениям c и d, тем богаче дугами соответствующий граф. Однако сравнение и выбор проводимые на основе очень малых требований могут не отразить реальную ситуацию выбора.
Поэтому необходимо последовательно и постепенно ослаблять требования к параметрам c,d,s и проанализировать возникающие связи.
Таким образом для каждой тройки c,d,s построенной граф, можно разделить на два непересекающихся подмножества.
Пусть 1-ое подмножество таково, что всякий элемент не включенный в него будет превзойден по крайней мере одним элементом ему принадлежащим.
Это свойство называется свойством внешней устойчивости.
Другое свойство данного подмножества в том, что никакой его элемент не превосходит другого элемента, т.е. они не сравнимы между собой при заданных параметрах c,d,s .
Подмножество вершин графа обладает этими 2-мя свойствами называется ядром.
Оно определяет набор лучших элементов или параметров.
c = 0,7
d = 0,4
e1, e2, e3, e4 – ядро
e2
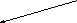
 e1
e3
e1
e3
e6 e4
e5
c = 0,6 d = 0,4 Ядро: e1, e3, e4
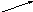
 e2
e2
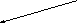
 e1
e3
e1
e3
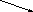 e6
e4
e6
e4
e5
По условию задачи ядро графа с параметрами 0,6 ; 0,4 ; 1 содержит вершины e1, e3, e4.
Можно проследить такую цепочку e3 > e6 > e5.
Если требуется обогатить граф дугами, то из-за невозможности ослабить требования к порогам соответствия и несоответствия необходимо обратиться к измерению параметра S и рассчитать матрицу несоответствия Сij(2)
-
Ядро графа может иметь различное число элементов. Если в ядре очень много элементов, это означает, что антагонизм критериев таков, что не позволяет сравнивать объект при этих параметрах. Усиление требовательности к порогам c и d сократит число элементов в ядре. В результате анализа поведения графов и их ядер можно выбрать небольшое число объектов, среди кот. находится и самый лучший. Иногда можно упорядочить объекты в некоторую последовательность благодаря кот. каждый объект сравнивается с другими и из них можно выбрать близкие или эквивалентные (циклически замкнутые) и прочие
Вопросы по теме 6
-
Сущность метода попарного сравнения альтернатив или метода многомерного выбора.
-
Что такое коэффициент согласия и как он определяется
-
Коэффициент несогласия и схема построения матрицы несогласия
-
Логика построения ядра с целью определения оптимальной альтернативы.
Для проведения практического занятия студентам предлагаются различные варианты в виде исходной таблицы с оценками экспертов различных альтернатив по 10 критериям, по результатам которой студент используя описанный выше метод РИПСА должен выбрать оптимальную альтернативу.
