34. Опуклі множини на площині

Поняття про опуклі функції, задані на проміжку, пов’язане з поняттям опуклої множини точок на площині.

Означення. Множина Е точок (х; у) площини називається опуклою, якщо для будь-яких двох різних точок (х₁; у₁) і (х₂; у₂) із Е відрізок, що сполучає ці точки, повністю належить множині Е.

Аналітично відрізком, кінцями якого є точки (х₁; у₁) і (х₂; у₂), будуть усі ті точки (х; у), координати яких задовольняють умову

(1)

При дістаємо точку (х₂; у₂), при — точку (х₁; у₁). Отже, якщо (х₁; у₁) і (х₂; у₂) — точки опуклої множини Е, то й точки ; будуть точками множини Е.

Прикладом опуклих множин на площині можна вважати саму площину, будь-яку пряму, проведену на площині або в півплощинах, на які площина поділяється прямою, множина точок площини, що лежить між двома паралельними прямими, кут на площині (якщо цей кут не перевищує ), опуклий многокутник, круг тощо.

Порожня множина або множина, що складається з однієї точки, також вважаються опуклими множинами.

Теорема 1. Переріз будь-якого числа опуклих на площині множин є опуклою множиною.

Точки (х; у) можна тлумачити не лише як точки площини з координатами х і у, а й як двовимірні вектори з координатами х і у. Тому, якщо дано два вектори і , то точки відрізка, що сполучає вектори і , є сукупністю векторів , які задовольняють умову

.

У координатній формі останню рівність можна записати у вигляді системи (1).

Означення. Множина Е називається опуклою, якщо для будь-яких двох векторів на площині із Е , і довільного дійсного числа вектор належить Е.

Довести, що множина

є опуклою.

• Нехай задано вектори і із Е та довільне , . Тоді , , , ,

де .

Із , , , випливає:

, ,

,

тобто , отже, належить Е і множина Е є опуклою.●

Показати, що множина

не є опуклою.

Візьмемо із множини Е два вектори і . Нехай , тоді вектор не належить Е, оскільки . Отже, Е не є опуклою множиною.

Зауваження. Будь-який замкнений, відкритий або напіввід­критий, скінченний або нескінченний проміжок є, очевидно, опуклою множиною.

35. Поняття про опуклі та вгнуті функції

Означення. Функція f(х) називається опуклою на проміжку [a, b], якщо множина

є опуклою.

Із означення бачимо, що А є така множина точок (х; у) площини, абсциси яких належать проміжку [a, b], а їх координати не менші від значення функції f(х) у точці х.

На рис. 5.23 зображено графіки функцій, опуклих на відрізку [a, b].

Рис. 5.23

Означення. Функція f(х) називається вгнутою на проміжку [a, b], якщо – f(х) є опуклою на тому самому проміжку.

Геометрична ілюстрація:

Рис. 5.24

На рис. 5.24 зображено графіки вгнутих функцій. Геометрично вгнута функція f(х) на проміжку (а; b) характеризується тим, що множина А розміщена не нижче від графіка у = f(х) на проміжку [a, b]. Вгнута функція f(х), навпаки, характеризується тим, що для неї множина А розміщена не вище від графіка у = f(х) на проміжку [a, b].

36. Ознаки опуклості та вгнутості функцій. Строго опуклі і строго вгнуті функції

Теорема 2 (перша ознака опуклості).

1. Для того щоб функція f(X) була опуклою на проміжку [a, b], необхідно і достатньо, аби виконувалася умова: для довільних х1 і х2 із [a, b] і будь-якого , 0    1

. (2)

2. Для того щоб функція f(х) була вгнутою на проміжку [а; b], необхідно і достатньо, аби виконувалася умова: для довільних х1 і х2 із [а; b] і будь-якого , 0    1

. (3)

Означення. 1. Функція f(х) на проміжку [a; b] називається опуклою (вгнутою), якщо для будь-яких двох точок х₁ і х₂ із [a; b] і будь-якого , 0    1, виконується нерівність

2. Функція f(x) на проміжку [a, b] називається строго опуклою (строго вгнутою), якщо для будь-яких точок х₁ і х₂ із [a, b], х₁  х₂, і будь-якого , 0 <  < 1, виконується нерівність

Геометрична ілюстрація

Рис. 5.25 Рис. 5.26

Геометрично умова (2) означає, що точки хорди, яка сполучає дві точки графіка опуклої функції f(x), лежать не нижче від графіка функції. Для строго опуклої функції точки такої хорди лежать вище від графіка функції, тобто якщо f(x) — строго опукла функція, то для будь-яких двох точок (х₁; f(x₁)) і (х₂; f(x₂)), х₁ < x < x₂, хорда, що сполучає ці дві точки, має задовольняти умову у > f(x).

У разі строго вгнутої функції f(x), навпаки, для точок (х; у) хорди, яка сполучає точки (х₁; f(x₁)), (х₂; f(x₂)) графіка у = f(x) має виконуватись умова у < f(x).

На рис. 5.25 і 5.26 подано графіки строго опуклої і строго вгнутої функцій.

Лінійна функція f(x) = аx + b опукла і одночасно вгнута (не строго), оскільки для неї одночасно виконуються умови (1) і (2), в яких нестрогі нерівності перетворюються на рівності.

Показати, що функція f(x) = x² строго опукла для дійсних х.

● Справді, нехай х₁ і х₂ — дійсні числа, х₁  х₂. Тоді

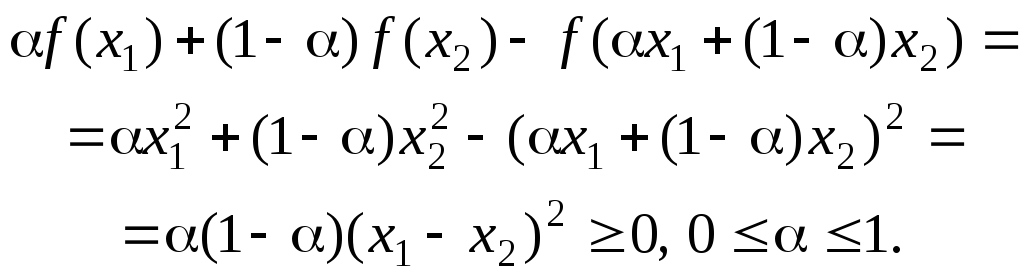
Отже, за умовою (1) функція f(x) = x² опукла; для x₁ = x² і 0 <  < 1 дістанемо строгу нерівність, звідки f(x) = x² — строго опукла функція.

Без доведення наведено такі ознаки опуклості.

Теорема 3 (друга ознака опуклості функції). Якщо f(x) опукла в інтервалі (a; b), то для будь-якої точки х₀  (a; b) функція

, (4)

монотонно зростаюча по х (неспадна). Якщо функція f(x) строго опукла, то F(x, x₀) — строго зростаюча.

Справджується й обернена теорема.

Теорема 4. Якщо функція f(x) задана в інтервалі (а; b) і для будь-якої точки функція

,

неспадна, то f(x) опукла (а; b), якщо строго зростаюча, то f(x) строго опукла на (а; b).

Теорема 5 (третя ознака опуклості функції). Функція f(x) строго опукла в інтервалі (а; b) тоді і тільки тоді, коли для будь-яких х₁ < x₂ < x₃ із (а; b).

.

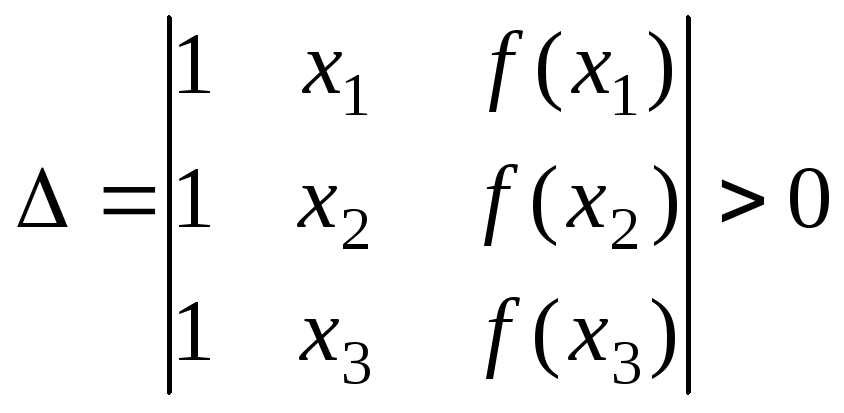Очевидно, що є критерієм для опуклої функції.

37. Критерії опуклості та вгнутості диференційовних функцій

Теорема 1. Для того щоб диференційовна в інтервалі (a; b) функція f(x) була опуклою (вгнутою), необхідно і достатньо, щоб її похідна f(x) у цьому інтервалі була монотонно зростаючою (монотонно спадною).

Дослідити функцію на опуклість.

● Маємо і похідну f(x) можна вважати і неспадною, і незростаючою. Тому функція f(x) опукла і вгнута не в строгому розумінні. ●

Знайти проміжки опуклості і вгнутості функції

.

● Оскільки , то задача зводиться до знаходження проміжків монотонності похідної f (x). Скориставшись умовами монотонності, знайдемо, що , звідки робимо висновки, що для і для х < 0.

Отже, f(x) зростає на проміжку (0; + ) і спадає на проміжку (–; 0). Звідси функція f(x) строго опукла на проміжну (0; + ) і спадає на проміжку (–; 0).

Теорема 2. Нехай функція f(x) двічі диференційовна на проміжку [a; b].

1) Для того щоб функція f(x) була опуклою (вгнутою) на проміжку [a; b], необхідно і достатньо, щоб для будь-якого х  [a; b].

2) Для того щоб f(x) була строго опуклою (строго вгнутою) на проміжку [a; b], необхідно і достатньо, щоб виконувалась попередня умова і щоб, крім того, не існувало інтервалу (с; d)  [a; b], в якому .

Означення. Диференційовна функція f(x) називається опуклою (вгнутою) в інтервалі (a; b), якщо в будь-якій точці графіка функції f(x) із інтервалу (a; b) дотична до графіка лежить не вище (не нижче) від графіка функції (рис. 5.27).

Означення. Диференційовна функція f(x) називається строго опуклою (строго вгнутою) в інтервалі (a; b), якщо в будь-якій точці графіка функції f(x) із інтервалу (a; b) дотична до графіка лежить нижче (вище) графіка функції f(x).