12. Равномерное движение материальной точки по окружности. Угловое перемещение, угловая скорость. Период и частота обращения, их единицы. Связь между линейной и угловой скоростью.
Равномерное движение материальной точки по окружности - движение материальной точки по окружности, при котором модуль ее скорости не меняется. При таком движении материальная точка обладает центростремительным ускорением.
Угловое перемещение - векторная величина, характеризующая изменение угловой координаты в процессе её движения.
Угловая
скорость - векторная
величина, характеризующая быстроту
вращения материальной точки. Вектор
угловой скорости по величине равен углу
поворота тела в единицу времени: 
Период вращения (Т) - время, за которое вращающееся тело совершает один полный оборот. T(c)=t/N
Частота
вращения - число полных
оборотов, совершаемых при равномерном
движении, за единицу времени. v(c-1)=N/t
13.
Нормальное и тангенциальное ускорение.
Угловое ускорение.
Движение материальной
точки по криволинейной траектории.
Радиус кривизны. Зависимость углового
перемещения и угловой скорости от
времени при постоянном угловом ускорении.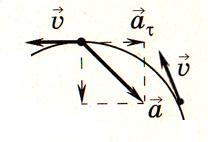
В общем случае ускорение направлено под углом к скорости. Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением . Она характеризует изменение скорости по модулю
.
Составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно (нормально) скорости, называется нормальным ускорением . Она характеризует изменение скорости по направлению
.
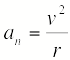Угловое ускорение - величина, характеризующая быстроту изменения угловой скорости. Измеряется в рад/сек2.
Условие
криволинейное движение организуется
если вектор силы (ускорения) не колониарен
вектору скорости. Движение по прямой
это частный случай движения по кривой
с радиусом.
14. Законы Ньютона. (Опыты, подтверждающие справедливость закона. Промышленное применение. Границы применимости законов). Инерциальные и неинерциальные системы отсчета. Инерция. Инертность тела.
1 закон Ньютона:
1. Существуют такие инерциальные системы отсчета, в которых равномерно движущееся или покоящееся материальная точка будет сохранять свое движение или покой при отсутствии сил или сумма сил скомпенсирована.
2. опыт:
равномерно движущийся автомобиль
3. промышленное применение:
строение станков
4. границы применения:
а) макромир и микромир
б) v << c c=3*108м/с
в)в ИСО
2 закон Ньютона:
1. Ускорение полученное материальной точкой прямо пропорционально силе приложенной к точке, и обратно пропорционально массе.
a
F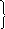
a F/m
a
1/m
EF - уравнение динамического равновесия.
2. опыт:
3. промышленное применение:
молот бьет по монете, монета действует на молот с такой же силой,
отдача.
4. границы применения:
а) макромир и микромир
б) v << c c=3*108м/с
в)в ИСО
3 закон Ньютона:
1. сила действия равна силе противодействия. Они равны по модулю и противоположны по знаку.
2. опыт:
3. промышленное применение:
молот бьет по монете, монета действует на молот с такой же силой,
отдача.
4. границы применения:
а) макромир и микромир
б) v << c c=3*108м/с
в) в ИСО
г) силы должны быть одной природы
Инерциальные системы отсчета - это системы, относительно которых материальная точка при отсутствии на нее внешних воздействий или их взаимной компенсации покоится или движется равномерно и прямолинейно.
Неинерциальная система отсчёта - произвольная система отсчёта, не являющаяся инерциальной. Примеры неинерциальных систем отсчета: система, движущаяся прямолинейно с постоянным ускорением, а также вращающаяся система.
1. Инерция - это явление сохранения скорости телом.
2. Связанно с равномерным движением или покоем.
3. На тело не должны действовать ни какие силы или действующие силы скомпенсированы.
4. Объясняется по 1 закону Ньютона.
5. На земле не применяется.
1. Инертность тела - это свойство тел сопротивляться изменению своей скорости.
2. Зависит от массы (прямо пропорционально) .
3. Условие: наличие силы
4. Объясняется по 2 закону Ньютона.
5. Насаживание ручек инструментов: топор, молоток, лопата.