
- •1. Векторные и скалярные величины. Действия над векторами.
- •2. Проекция вектора на координатные оси. Действия над проекциями.
- •3. Основная задача механики. Поступательное движение. Материальная точка. Положение тела в пространстве. Тело отсчета, система отсчета.
- •4. Траектория, путь, перемещение. Средняя скорость. Относительность движения. Закон сложения скоростей.
- •5. Прямолинейное равномерное движение, уравнения движения и графики: х(t), VX(t), s(t).
- •6. Скорость при неравномерном движении. Средняя путевая скорость, средняя скорость движения. Мгновенная скорость.
- •7. Ускорение, единицы измерения ускорения. Равнопеременное движение. Уравнения движения и графики: х(t), VX(t), аx(t).
- •8. Ускорение, среднее ускорение. Нормальное и тангенциальное ускорение.
- •9. Свободное падение. Движение тела, брошенного вертикально вверх. Ускорение свободного падения. Уравнения движения и графики: у(t), vу(t), ау(t).
- •10. Движение тела, брошенного горизонтально. Уравнения движения и графики: х(t), у(t), VX(t), vy(t) , аx(t), ау(t). Уравнение траектории.
- •12. Равномерное движение материальной точки по окружности. Угловое перемещение, угловая скорость. Период и частота обращения, их единицы. Связь между линейной и угловой скоростью.
- •15. Сила, масса, их единицы измерения. Виды сил в природе. Принцип относительности Галилея.
- •16. Деформация тел. Сила упругости. Закон Гука, коэффициент жёсткости, механическое напряжение, относительное удлинение, модуль Юнга.
- •2. Опыт:
- •3. Промышленное применение:
- •4. Границы применения:
- •18. Cила тяжести. Измерение массы тел взвешиванием. Вес тела, невесомость. Движение с ускорением.
- •19. Искусственные спутники Земли. Первая космическая скорость.
7. Ускорение, единицы измерения ускорения. Равнопеременное движение. Уравнения движения и графики: х(t), VX(t), аx(t).
Ускорение - это отношение разности скоростей к промежутку времени за которое оно пройдено.
a=vк-vн/∆t. Измеряется в м/с2.
Равнопеременное движение — движение с постоянным ускорением.
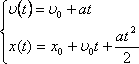 .
.
8. Ускорение, среднее ускорение. Нормальное и тангенциальное ускорение.
Ускорение - это отношение разности скоростей к промежутку времени за которое оно пройдено.
a=vк-vн/∆t. Измеряется в м/с2.
|
∆u ∆t |
acред=
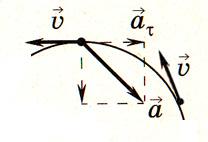
В общем случае ускорение направлено под углом к скорости. Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением . Она характеризует изменение скорости по модулю
![]() .
.
Составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно (нормально) скорости, называется нормальным ускорением . Она характеризует изменение скорости по направлению
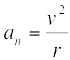 .
.
9. Свободное падение. Движение тела, брошенного вертикально вверх. Ускорение свободного падения. Уравнения движения и графики: у(t), vу(t), ау(t).
Свободное падение - равноускоренное движение, под действием силы тяжести, при отсутствии сопротивления воздуха.
Тело, брошенное вертикально вверх, движется равномерно замедленно с начальной скоростью u0 и ускорением a = -g. Перемещение тела за время t представляет собой высоту подъема h.
Для этого движения справедливы формулы:
Если:
u0 — начальная скорость движения тела ,
u — скорость падения тела спустя время t,
g — ускорение свободного падения, 9.81 (м/с²),
h — высота на которую поднимется тело за время t,
t — время,
То, движение тела, брошенного вертикально вверх описывается следующими формулами:
Высота подъема тела за некоторое время, зная конечную скорость: h=(u0+ u)t/2;
Высота подъема тела за некоторое время, зная ускорение свободного падения: h=u0t−(gt2/2);
Скорость тела через некоторое время, зная ускорение свободного падения: u=u0−gt;
Скорость тела на некоторой высоте, зная ускорение свободного падения: u=u02−2gh;
Максимальная высота подъема тела, зная первоначальную скорость и ускорение свободного падения: hmax=u02/2g;
Время подъема на максимальную высоту подъема тела, зная первоначальную скорость и ускорение свободного падения: thmax=u0/g;
В
соответствии со вторым законом Ньютона,
ускорение свободного
падения равно силе тяжести, действующей
на объект единичной массы
![]() .
.
10. Движение тела, брошенного горизонтально. Уравнения движения и графики: х(t), у(t), VX(t), vy(t) , аx(t), ау(t). Уравнение траектории.
Движение
тела, брошенного горизонтально,
представляет собой комбинацию двух
движений, взаимно перпендикулярных
друг другу: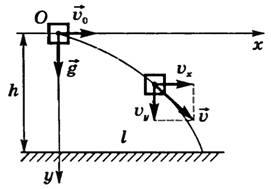
— горизонтального (равномерного) движения,
— вертикального (свободного падения)
![]()
![]()
Уравнение
траектории тела,
брошенного горизонтально выглядит
следующим образом:
![]() ;
;
11. Движение тела, брошенного под углом к горизонту. Уравнения движения и графики: х(t), у(t), vx(t), vy(t), аx(t), ау(t). Уравнение траектории. Вывод формул времени полёта, дальности полёта, максимальной высоты подъема.
Движение тела, брошенного под углом к горизонту, представляет собой комбинацию двух поступательных движений:
— Равномерное прямолинейное движение под углом α к горизонту,
— Свободное падение в вертикальном направлении.
Общее время движения тела, брошенного под углом к горизонту в два раза больше времени максимального
подъема (время подъема равно времени падения): tsmax= 2 thmax= 2u0sin(α)/g;
Дальность броска или радиус поражения определяется по формуле: Smax=u02sin(2α)/g;
Максимальная высота подъема тела, брошенного под углом к горизонту определяется по формуле: hmax=(u0sin(α))2/2g;
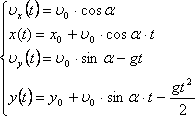
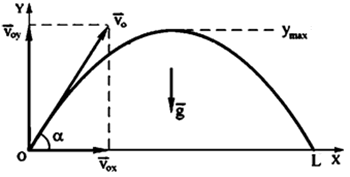
В наивысшей точки траектории проекция скорости на ось y меняет знак (тело меняет направление движение) и равна нулю: xy(t)=0 .
В самой дальней точке траектории координата y обращается в ноль: y(t)=0.
Уравнение движения тела, брошенного под углом к горизонту: y=xtg(α)−(g/2u02cos(α)2)x2;
Для
того чтобы получить уравнение
траектории, выразим
время t из уравнения координаты x и
подставим в уравнение для y: 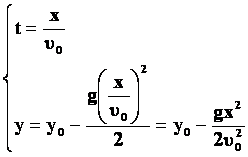
- между координатами квадратичная зависимость, траектория – парабола!
