
- •I курс, I Семестр.
- •Содержание: Вопрос № 1 Понятие «Множества»:
- •Операции над множествами:
- •Числовая прямая:
- •Ограниченность числового множества:
- •Теорем о существовании точных верхней и нижней граней:
- •Некоторые характеристики Rn:
- •Вопрос № 3 Понятие функции, как отображения:
- •Классификация функций:
- •Вопрос № 4 Числовая последовательность:
- •Критерий Коши сходимости последовательности:
- •Вопрос № 5 Теорема о единственности предела последовательности:
- •Вопрос № 6 Теорема об ограниченности сходящейся последовательности:
- •Теорема: Сходящаяся последовательность ограничена:
- •Вопрос № 7 Монотонные последовательности:
- •Вопрос № 8 Бесконечно малые последовательности и их свойства:
- •Свойства бесконечно большой последовательности:
- •Вопрос № 12 Предел функции:
- •Свойства непрерывных функций:
- •Вопрос № 18: Понятие сложной функции:
- •Вопрос № 19: Классификация точек разрыва:
- •Вопрос № 32: Экстремумы:
- •Локальные экстремумы:
- •Необходимое условие экстремума:
- •Достаточное условие экстремума:
- •Достаточное условие экстремума:
- •Вопрос № 34: Направление выпуклости графика функции:
- •Достаточное условие выпуклости графика функции:
- •Вопрос № 35: Точки перегиба графика функции:
- •Необходимое условие точки перегиба:
- •Общий случай:
- •Вопрос № 36: Асимптоты графика функции:
- •Вопрос № 37: Понятие п-мерной точки, п-мерного пространства:
- •Вопрос № 38: Частные производные:
- •Дифференцирование функции многих переменных:
- •Понятие частных дифференциалов:
- •Геометрический смысл частных производных:
- •Вопрос № 39: Дифференцируемость функции
- •Необходимые условия дифференцирования:
- •Достаточные условия дифференцирования:
- •Вопрос № 40: Производная по направлению:
- •Вопрос № 43: Понятие о функциях, заданных неявно:
- •Касательная и нормаль к поверхности:
- •Вопрос № 44: Частные производные высших порядков:
- •Необходимое условие существования экстремума:
- •Вопрос № 46: Первообразная:
- •Теорема о среднем:
- •Вопрос № 54: Определённый интеграл с переменным верхним пределом:
- •Свойства.
- •Свойства.
Критерий Коши сходимости последовательности:
Для
сходимости последовательности необходимо
и достаточно для всех ε>0 что бы
существовал N такой,
что при всех п> Nε
при всех
![]() .
.
![]()
Вопрос № 5 Теорема о единственности предела последовательности:
Сходящаяся последовательность имеет только один предел.
Предположим
![]() и
и
![]() .
Для определённости положим
.
Для определённости положим
![]() .
.
Возьмём
![]() ,
тогда существует N1
такой, что при всех п>N1
выполняется
,
тогда существует N1
такой, что при всех п>N1
выполняется
![]() и
существует N2
такой, что при всех п>N2
выполняется
и
существует N2
такой, что при всех п>N2
выполняется
![]()
Пусть
![]() ,
тогда п>N.
Одновременное выполнение
,
тогда п>N.
Одновременное выполнение
![]() и
п>N2, что
невозможно даже при указанном ε
ε-окрестность, так как а и в не
пересекаются.
и
п>N2, что
невозможно даже при указанном ε
ε-окрестность, так как а и в не
пересекаются.
Полученное противоречие доказывает единственность предела.
![]()
Вопрос № 6 Теорема об ограниченности сходящейся последовательности:
Последовательность
Хп называется ограниченной,
если существует точка М из R
такая, что
![]() при
всех п, а так же есть А>0 такая,
что
при
всех п, а так же есть А>0 такая,
что
![]() /
/
Последовательность
хп называется неограниченной,
если для всех А>0 (сколько угодно
больших) есть N такое,
что
![]() .
.
Теорема: Сходящаяся последовательность ограничена:
Доказательство:
![]() для
ε=1 есть Nε
такой, что при всех N>Nε
для
ε=1 есть Nε
такой, что при всех N>Nε
![]()
![]() ,
тогда для п > Nε:
,
тогда для п > Nε:
![]()
![]() ,
то при всех п
,
то при всех п
![]() .
.
![]()
Вопрос № 7 Монотонные последовательности:
-
Монотонные последовательности.
-
Теорема о сходимости монотонной последовательности.
{xn} называется возрастающей, если для всех п1, п2 таких, что п1<п2: х1<x2, и не убывает, если для всех п1, п2 таких, что п1<п2: х1<=x2
{xn} называется убывающей, если для всех п1, п2 таких, что п1<п2: х1>x2, и не убывает, если для всех п1, п2 таких, что п1<п2: х1>=x2
Теорема: Возрастающая последовательность ограничена сверху и имеет конечный предел. Убывающая последовательность ограничена снизу и имеет конечный предел.
Доказательство:
(Возрастающая последовательность
ограничена сверху и имеет конечный
предел.): хп1<xn2
при любых п1<п2
и хп<=М при любых
п.
По теореме об ограниченном
множестве есть число
![]() ,
то есть хп<=а, а так
же для всех ε>0 найдётся N
такой, что
,
то есть хп<=а, а так
же для всех ε>0 найдётся N
такой, что
![]() .
Тогда при всех п>N
.
Тогда при всех п>N
![]() ,
или
,
или
![]() ,
тогда при n>N
,
тогда при n>N
![]() ,
другими словами
,
другими словами
![]() .
(Убывающая
последовательность ограничена снизу
и имеет конечный предел): хп1>xn2
при любых п1<п2
и хп>=m
при любых п. По теореме об ограниченном
множестве есть число
.
(Убывающая
последовательность ограничена снизу
и имеет конечный предел): хп1>xn2
при любых п1<п2
и хп>=m
при любых п. По теореме об ограниченном
множестве есть число![]() ,
то есть хп<=а, а так
же для всех ε>0 найдётся N
такой, что
,
то есть хп<=а, а так
же для всех ε>0 найдётся N
такой, что![]() .
Тогда при всех п>N
–
.
Тогда при всех п>N
–
![]()
![]()
Вопрос № 8 Бесконечно малые последовательности и их свойства:
Последовательность
бесконечно малая,
если для всех ε>0 найдётся Nε
такой, что при всех п> Nε
![]()
Свойства бесконечно большой последовательности:
-
Сумма двух бесконечно малых последовательностей даёт бесконечно малую последовательность.
-
Пусть
 ,
тогда рассмотрим сумму этих двух
последовательностей: По условию ε>0
найдётся N1
такой, что всех п>N1
,
тогда рассмотрим сумму этих двух
последовательностей: По условию ε>0
найдётся N1
такой, что всех п>N1
 и
найдётся N2
такой, что всех п>N2
и
найдётся N2
такой, что всех п>N2
-
 ,
тогда при всех п>N:
,
тогда при всех п>N:
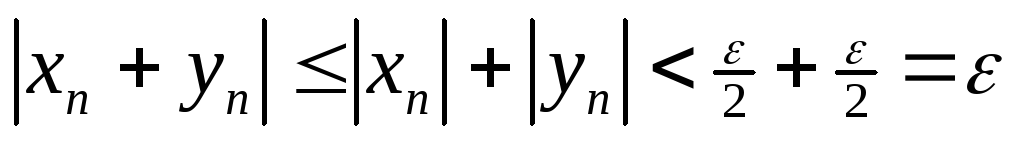
-
-
Разность двух бесконечно малых последовательностей – бесконечно малая последовательность.
-
Следствие: Алгебраическая сумма бесконечно малой величины – есть бесконечно малая величина.
-
-
Бесконечно малая последовательность ограничена, так как являет собой частный случай сходящейся последовательности.
-
Произведение бесконечно малой последовательности на ограниченную – есть бесконечно малая последовательность
-
Пусть
 и
при всех п:
и
при всех п:
 .
Возьмём ε>0, тогда найдётся Nε
такой, что при всех п> Nε
.
Возьмём ε>0, тогда найдётся Nε
такой, что при всех п> Nε
 .
Оценим
.
Оценим

-
Следствие: произведение конечного числа бесконечно малых последовательностей – есть бесконечно малая последовательность.
-
-
-
Если все элементы бесконечно малой последовательности одному и тому же С, то С=0.
-
Если
 – бесконечно большая, то обратная к
ней – бесконечно малая.
– бесконечно большая, то обратная к
ней – бесконечно малая.
![]()
Вопрос № 9 Бесконечно большие последовательности и их свойства:
-
Бесконечно большие последовательности и их свойства.
-
Связь между бесконечно большими и бесконечно малыми последовательностями.
-
Последовательность
бесконечно большая,
если для всех А>0 найдётся N
такой, что при всех п> N
![]() .
.
Свойства бесконечно малой последовательности:
-
Сумма бесконечно больших последовательности одного знака – бесконечно большая последовательность.
-
Разность даёт неопределённое выражение.
-
Произведение двух бесконечно больших последовательностей – бесконечно большая последовательность.
-
Отношение двух бесконечно больших последовательностей не определена.
Связь между бесконечно большими и бесконечно малыми последовательностями:
![]() Действительно
Действительно
![]() ,
однозначно для каждого ε>0 найдётся
Nε такой, что
при всех п> Nε
,
однозначно для каждого ε>0 найдётся
Nε такой, что
при всех п> Nε
![]()
![]()
Вопрос № 10 Теорема об арифметических действиях над последовательностями, имеющими конечный предел:
![]() тогда:
тогда:
-
 .
Доказательство:
.
Доказательство:
 –
обозначим
–
обозначим
 при
п стремящемся к нулю.
при
п стремящемся к нулю.
 –
обозначим
–
обозначим
 при
п стремящемся к нулю.
Докажем,
что
при
п стремящемся к нулю.
Докажем,
что
 –
бесконечно мала:
–
бесконечно мала:
 –
бесконечно малая величина.
–
бесконечно малая величина. -

-
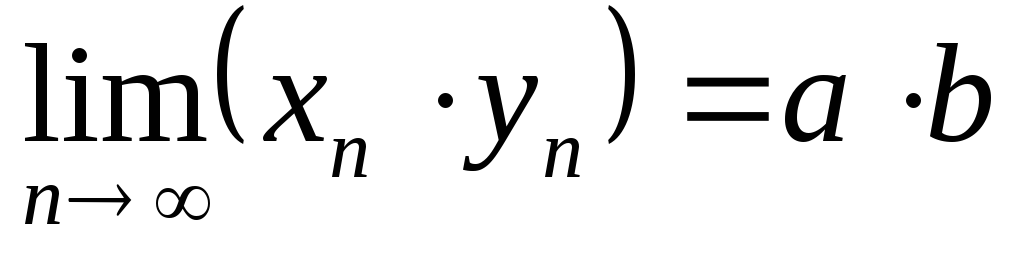
-

![]()
Вопрос № 11 Теоремы о переходе к пределу в неравенствах:
-
Пусть
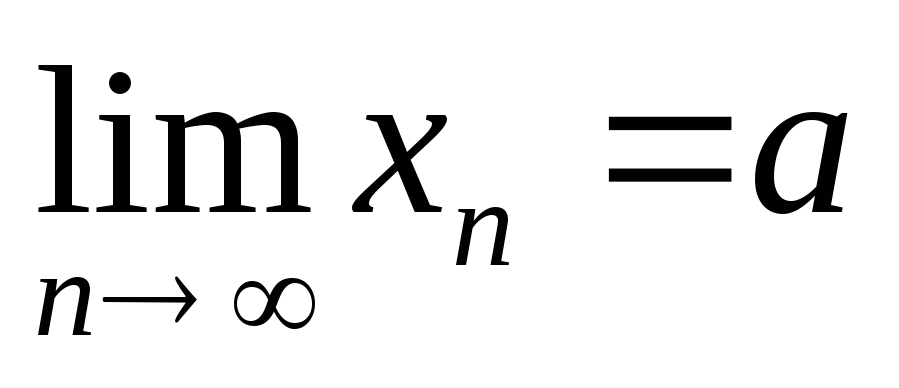 и
при n>N
и
при n>N
 .
Доказательство:
Предположим a<b,
то есть b-a>0.
Возьмём
.
Доказательство:
Предположим a<b,
то есть b-a>0.
Возьмём
 ,
для него существует Nε
такой, что при всех п> Nε>=N:
,
для него существует Nε
такой, что при всех п> Nε>=N:
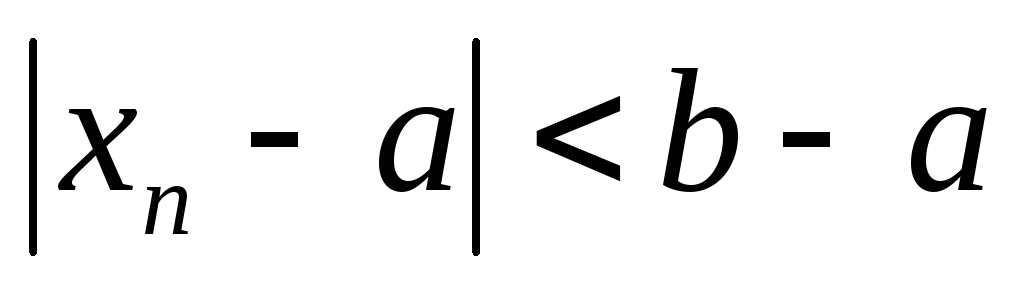 ,
или
,
или
 –
противоречие показывает, что
–
противоречие показывает, что

-
Пусть
 и
при n>N
и
при n>N
 .
Доказательство:
Предположим a<b,
то есть b-a<0.
Возьмём
.
Доказательство:
Предположим a<b,
то есть b-a<0.
Возьмём
 ,
для него существует Nε
такой, что при всех п> Nε>=N:
,
для него существует Nε
такой, что при всех п> Nε>=N:
 ,
или
,
или
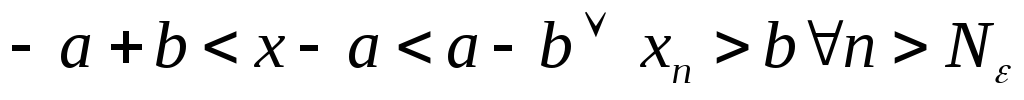 –
противоречие показывает, что
–
противоречие показывает, что

Следствия:
-
Пусть
 и
для всех
и
для всех

-
Пусть
 и
для всех
и
для всех

-
Пусть
 и для всех
и для всех
 –
сходится, и
–
сходится, и

![]()
