1. Перетворити у ланцюговий дріб число . Знайти підхідний дріб .

Розв’язання.

! Теоретичні відомості !

Ланцюговим дробом називається дріб 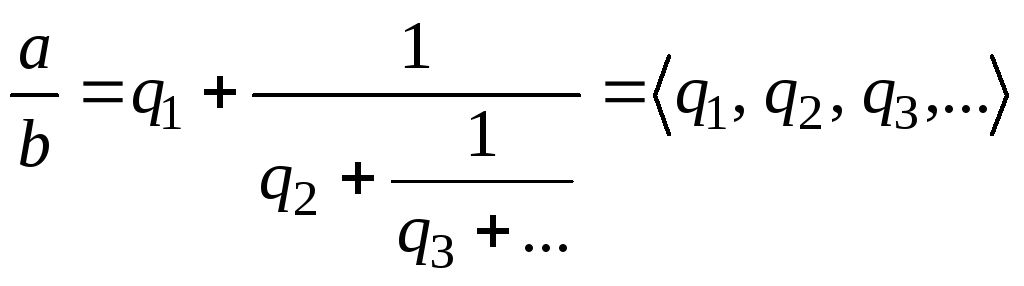, де – неповні частки.

! Теоретичні відомості !

Цілою частиною числа називається найбільше ціле число, що не перевищує . Дробовою частиною числа називається число, що дорівнює .

! Теоретичні відомості !

Неповні частки ланцюгового дробу для числа можна знаходити наступним чином:

, ,

якщо вважати, що .

Знайдемо неповні частки для заданого числа :

,

,

.

Легко бачити, що , а тобто й . Неважко показати, що .

Таким чином, .

! Теоретичні відомості !

Підхідним дробом називається дріб .

! Теоретичні відомості !

Чисельники й знаменники підхідних дробів пов’язані наступними рекурентними співвідношеннями:

, .

Усі підхідні дроби можна знайти безпосередньо з їх запису, але на практиці зручніше користуватися наступною таблицею. Для того, щоб заповнити пусту клітину, необхідно число, яке стоїть у другому рядку над незаповненою клітиною, помножити на число, що стоїть зліва від незаповненої клітини й додати наступне число, що стоїть зліва.

	– 1	0	1	2	3	4	5
	–	–	6	12	12	12	12
	0	1	6	73	882	10657	128766
	1	0	1	12	145	1752	21169

Наприклад, чисельник першого підхідного дробу знаходиться наступним чином:

.

Отже, .

Відповідь. , .

2. За даним скінченним ланцюговим дробом знайти відповідний звичайний нескоротній дріб і всі його підхідні дроби.

Розв’язання. З умови зрозуміло, що , , , та . Для знаходження підхідних дробів складаємо таблицю:

	– 1	0	1	2	3	4	5
	–	–	3	2	5	8	1
	0	1	3	7	38	311	349
	1	0	1	2	11	90	101

Отже, , , , , , .

Відповідь. , , , , , .

3. Записати нескінчений періодичний дріб у вигляді квадратичної ірраціональності.

Розв’язання.

! Теоретичні відомості !

Вираз , якщо число не є точним квадратом, називається квадратичною ірраціональністю.

Уведемо наступне позначення:

.

Знайдемо значення , а для цього визначимо підхідні дроби для ланцюгового дробу :

	– 1	0	1	2	3
	–	–	4	2
	0	1	4	9
	1	0	1	2

Тобто .

Розв’яжемо отримане рівняння відносно . Після перетворень отримаємо наступне квадратне рівняння:

.

Його корені , . З отриманих значень обираємо те, ціла частина якого дорівнює 4, оскільки . Отже .

Далі виразимо число через , для чого знайдемо підхідні дроби

	– 1	0	1	2	3	4
	–	–	0	1	3
	0	1	0	1	1
	1	0	1	1	4

Тобто

.

Відповідь. .