
- •Завдання Контрольна робота № 1 «Комплексні числа»
- •Контрольна робота № 2 «Цілі числа. Числові функції»
- •Контрольна робота № 3 «Порівняння»
- •Розв’язання типового варіанта
- •1. Комплексне число представити в тригонометричній і показниковій формах.
- •2. Комплексне число представити у вигляді . Навести геометричну інтерпретацію.
- •3. Знайти множину точок на площині комплексного змінного , яка визначається наступними умовами (графічно).
- •4. Скласти квадратне рівняння, яке має корені . Розв’язати його.
- •5. Записати дану тригонометричну функцію
- •1. Для чисел та :
- •2. Для числа знайти значення функції Ейлера від , суму й число усіх натуральних дільників.
- •1. З’ясувати, чи є система залишків за модулем повною. Побудувати приведену систему залишків за цим модулем.
- •2. Перевірити, чи має порівняння першого степеня розв’язки. У разі позитивної відповіді розв’язати порівняння методом випробування повної системи залишків.
- •3. Методом алгебраїчних перетворень знайти розв’язки порівняння першого степеня .
- •4. Знайти останню цифру числа .
- •5. Використовуючи метод Ейлера знайти розв’язок порівняння першого степеня .
- •6. Розв’язати систему порівнянь першого степеня за допомогою китайської теореми про залишки та за допомогою алгебраїчних перетворень.
- •1. Обчислити символ Лежандра .
- •2. Перевірити, чи має розв’язок порівняння .
- •3. Перевірити, чи є число 3 первісним коренем за модулем 7. У разі позитивної відповіді побудувати таблицю індексів за даним модулем.
- •4. За допомогою індексів розв’язати порівняння
- •1. Перетворити у ланцюговий дріб число . Знайти підхідний дріб .
- •2. За даним скінченним ланцюговим дробом знайти відповідний звичайний нескоротній дріб і всі його підхідні дроби.
- •3. Записати нескінчений періодичний дріб у вигляді квадратичної ірраціональності.
- •4. Розв’язати порівняння першого степеня за допомогою ланцюгових дробів.
- •1. Використовуючи схему Горнера, обчислити та розкласти многочлен за степенями , якщо .
- •2. Визначити всі раціональні корені многочлена .
- •3. Використовуючи метод Кардана, розв’язати кубічне рівняння .
- •4. Методом Феррарі знайти розв’язки рівняння четвертого степеня .
- •1. Відділити кратні корені многочлена .
- •2. За допомогою теореми Штурма відділити дійсні корені многочлена .
- •3. Довести незвідність многочлена над полем , використовуючи критерій Ейзенштейна.
- •4. Симетричний многочлен від трьох змінних виразити через елементарні.
- •5. Знайти значення виразу , де – корені многочлена .
- •Література
5. Використовуючи метод Ейлера знайти розв’язок порівняння першого степеня .
Розв’язання. Як було показано вище, дане порівняння має один розв’язок.
! Теоретичні відомості !
Метод
Ейлера.
Для порівняння
![]() ,
де
,
де
![]() ,
розв’язок можна знаходити за формулою:
,
розв’язок можна знаходити за формулою:
![]() .
.
У
нашому випадку,
![]() ,
,
![]() ,
,
![]() .
Оскільки
.
Оскільки
![]() ,
то умови застосування методу Ейлера
виконані. Шуканий розв’язок
,
то умови застосування методу Ейлера
виконані. Шуканий розв’язок
![]() .
.
Функція
Ейлера
![]() .
Отже,
.
Отже,
![]()
![]() .
.
Відповідь.
![]() .
.
6. Розв’язати систему порівнянь першого степеня за допомогою китайської теореми про залишки та за допомогою алгебраїчних перетворень.
Розв’язання. Розв’яжемо задану систему за допомогою китайської теореми про залишки.
! Теоретичні відомості !
Китайська
теорема про залишки.
Якщо числа
![]() попарно взаємно прості, то система
порівнянь
попарно взаємно прості, то система
порівнянь
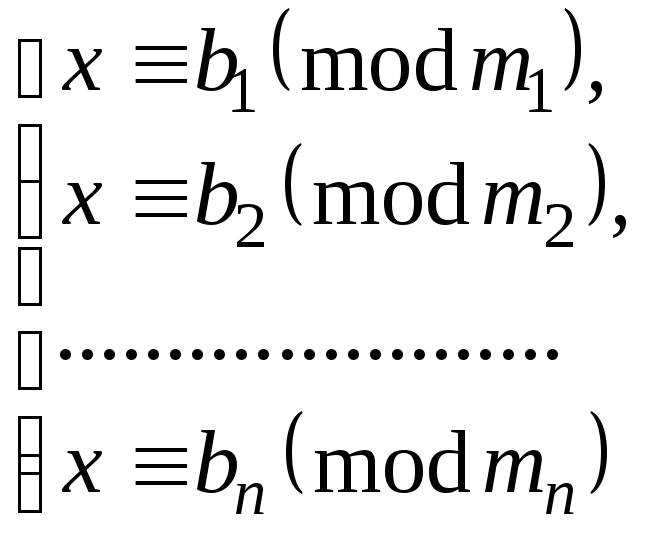 завжди має розв’язок. Будь-які два
розв’язки відрізняються на число, яке
кратне
завжди має розв’язок. Будь-які два
розв’язки відрізняються на число, яке
кратне
![]() .
.
Приведемо задану систему до стандартного виду:
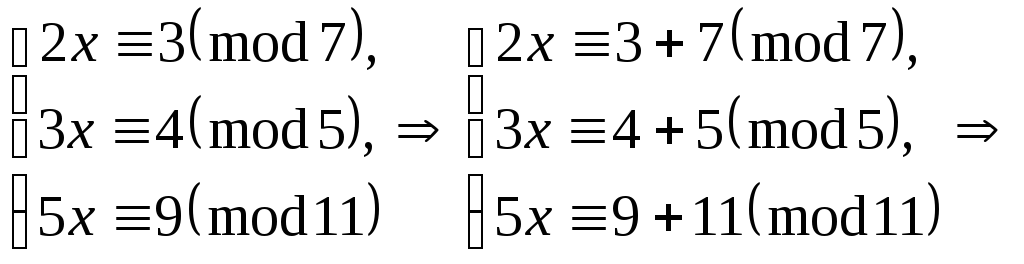
У
даному випадку
![]() ,
,
![]() ,
а також
,
а також
![]() ,
,
![]() ,
,
![]() ,
тобто всі модулі являються попарно
взаємно простими.
,
тобто всі модулі являються попарно
взаємно простими.
Будуємо таблицю:
|
|
1 |
2 |
3 |
|
|
7 |
5 |
11 |
|
|
55 |
77 |
35 |
Тут
![]() – модулі у системі порівнянь,
– модулі у системі порівнянь,
![]() – добуток усіх модулів, окрім
– добуток усіх модулів, окрім
![]() .
Тобто для даної системи, наприклад,
.
Тобто для даної системи, наприклад,
![]() .
.
Знайдемо
тепер лінійне представлення НСД чисел
![]() та
та
![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Випишемо підкреслені доданки у отриманих розкладах НСД:
![]() ,
,
![]() ,
,
![]() .
.
Розв’язком заданої системи порівнянь є клас
![]()
![]()
![]() .
.
Знайдемо тепер розв’язок вихідної системи за допомогою арифметичних перетворень.
! Теоретичні відомості !
Метод алгебраїчних перетворень розв’язання системи порівнянь полягає у наступному: спочатку розв’язуємо перше порівняння системи і з його розв’язків обираємо ті, що задовольняють другому порівнянню. Серед спільних розв’язків перших двох порівнянь знаходимо ті, що задовольняють третьому порівнянню і так далі, поки не буде знайдено розв’язок для усіх порівнянь системи.
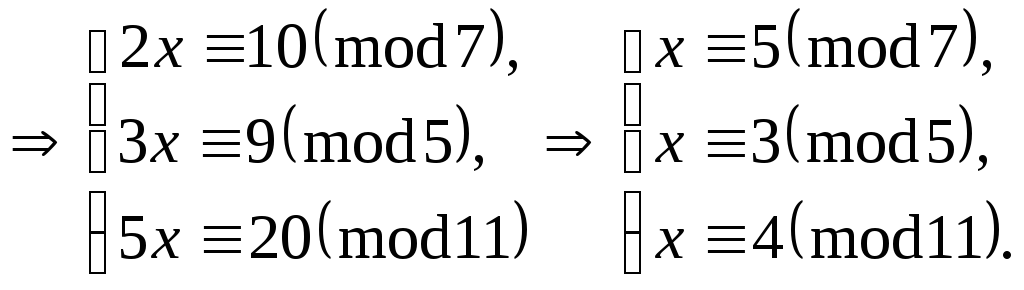
Спочатку
знайдемо розв’язок першого порівняння
системи
![]() будь-яким методом, наприклад, за допомогою
метода алгебраїчних перетворень.
будь-яким методом, наприклад, за допомогою
метода алгебраїчних перетворень.
Перевіримо,
чи має дане порівняння розв’язки:
![]() – один клас розв’язків. Знайдемо його:
– один клас розв’язків. Знайдемо його:
![]() .
.
Підставляємо
отриманий розв’язок у друге порівняння
системи
![]() :
:
![]() .
.
Так
як
![]() ,
то порівняння має розв’язок. Знаходимо
його:
,
то порівняння має розв’язок. Знаходимо
його:
![]()
![]() .
.
Отже,
![]() .
Цей спільний розв’язок перших двох
порівнянь системи підставляємо у третє
.
Цей спільний розв’язок перших двох
порівнянь системи підставляємо у третє
![]() :
:
![]() .
.
Робимо
перевірку розв’язності:
![]() – порівняння має один клас розв’язків.
І за допомогою алгебраїчних перетворень
коефіцієнтів отримуємо:
– порівняння має один клас розв’язків.
І за допомогою алгебраїчних перетворень
коефіцієнтів отримуємо:
![]()
![]() .
.
Таким чином,
![]()
або, що теж саме,
![]() .
.
Відповідь.
![]() .
.
Контрольна робота № 4
1. Обчислити символ Лежандра .
Розв’язання.
! Теоретичні відомості !
Символом
Лежандра називається
вираз виду
![]() ,
де
,
де
![]() – просте непарне число,
– просте непарне число,
![]() ,
який приймає значення 1 або – 1 у залежності
від того, має чи не має розв’язок
порівняння
,
який приймає значення 1 або – 1 у залежності
від того, має чи не має розв’язок
порівняння
![]() .
.
! Теоретичні відомості !
Властивості символу Лежандра:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() .
4)
.
4)
![]() ;
5)
;
5)
![]() .
.
6)
![]() ;
7)
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ,
,
![]() – прості непарні числа.
– прості непарні числа.
Так
як
![]() ,
то згідно з другою властивістю символів
Лежандра
,
то згідно з другою властивістю символів
Лежандра
![]() .
.
Так як 61 та 197 – прості непарні числа, то за дев’ятою властивістю
![]() .
.
З
того, що
![]() ,
маємо що
,
маємо що
![]() .
.
За
властивістю 5), оскільки
![]() ,
можемо записати:
,
можемо записати:
![]() .
.
Використовуючи властивість 7), обчислюємо
![]() .
.
А за властивістю 9):
![]() .
.
Тобто
![]()
![]() .
.
Відповідь.
![]() .
.
