
- •Завдання Контрольна робота № 1 «Комплексні числа»
- •Контрольна робота № 2 «Цілі числа. Числові функції»
- •Контрольна робота № 3 «Порівняння»
- •Розв’язання типового варіанта
- •1. Комплексне число представити в тригонометричній і показниковій формах.
- •2. Комплексне число представити у вигляді . Навести геометричну інтерпретацію.
- •3. Знайти множину точок на площині комплексного змінного , яка визначається наступними умовами (графічно).
- •4. Скласти квадратне рівняння, яке має корені . Розв’язати його.
- •5. Записати дану тригонометричну функцію
- •1. Для чисел та :
- •2. Для числа знайти значення функції Ейлера від , суму й число усіх натуральних дільників.
- •1. З’ясувати, чи є система залишків за модулем повною. Побудувати приведену систему залишків за цим модулем.
- •2. Перевірити, чи має порівняння першого степеня розв’язки. У разі позитивної відповіді розв’язати порівняння методом випробування повної системи залишків.
- •3. Методом алгебраїчних перетворень знайти розв’язки порівняння першого степеня .
- •4. Знайти останню цифру числа .
- •5. Використовуючи метод Ейлера знайти розв’язок порівняння першого степеня .
- •6. Розв’язати систему порівнянь першого степеня за допомогою китайської теореми про залишки та за допомогою алгебраїчних перетворень.
- •1. Обчислити символ Лежандра .
- •2. Перевірити, чи має розв’язок порівняння .
- •3. Перевірити, чи є число 3 первісним коренем за модулем 7. У разі позитивної відповіді побудувати таблицю індексів за даним модулем.
- •4. За допомогою індексів розв’язати порівняння
- •1. Перетворити у ланцюговий дріб число . Знайти підхідний дріб .
- •2. За даним скінченним ланцюговим дробом знайти відповідний звичайний нескоротній дріб і всі його підхідні дроби.
- •3. Записати нескінчений періодичний дріб у вигляді квадратичної ірраціональності.
- •4. Розв’язати порівняння першого степеня за допомогою ланцюгових дробів.
- •1. Використовуючи схему Горнера, обчислити та розкласти многочлен за степенями , якщо .
- •2. Визначити всі раціональні корені многочлена .
- •3. Використовуючи метод Кардана, розв’язати кубічне рівняння .
- •4. Методом Феррарі знайти розв’язки рівняння четвертого степеня .
- •1. Відділити кратні корені многочлена .
- •2. За допомогою теореми Штурма відділити дійсні корені многочлена .
- •3. Довести незвідність многочлена над полем , використовуючи критерій Ейзенштейна.
- •4. Симетричний многочлен від трьох змінних виразити через елементарні.
- •5. Знайти значення виразу , де – корені многочлена .
- •Література
4. Симетричний многочлен від трьох змінних виразити через елементарні.
Розв’язання.
! Теоретичні відомості !
Симетричний
многочлен –
многочлен від
![]() змінних
змінних
![]() ,
який не змінюється при всіх перестановках
змінних, що входять до його запису.
,
який не змінюється при всіх перестановках
змінних, що входять до його запису.
! Теоретичні відомості !
До елементарних симетричних многочленів відносять наступні, наприклад, елементарні многочлени від трьох змінних:
![]() ,
,
![]() ,
,
![]() .
.
! Теоретичні відомості !
Основна
теорема теорії симетричних многочленів.
Будь-який симетричний многочлен від
![]() змінних можна представити у вигляді
многочлена від елементарних симетричних
многочленів, причому таке представлення
єдине.
змінних можна представити у вигляді
многочлена від елементарних симетричних
многочленів, причому таке представлення
єдине.
Обираємо
одночлен, у якому
![]() стоїть в максимальному степені (якщо
таких одночленів декілька, то з них
обираємо той, у якому
стоїть в максимальному степені (якщо
таких одночленів декілька, то з них
обираємо той, у якому
![]() має максимальну степінь і так далі). Для
заданого симетричного многочлена таким
є одночлен
має максимальну степінь і так далі). Для
заданого симетричного многочлена таким
є одночлен
![]() .
Випишемо всілякі набори
.
Випишемо всілякі набори
![]() ,
які задовольняють наступним умовам:
,
які задовольняють наступним умовам:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
Для
кожного такого набору вказуємо симетричний
многочлен виду
![]() ,
де
,
де
![]() ,
,
![]() ,
,
![]() .
Для зручності складемо таблицю:
.
Для зручності складемо таблицю:
|
Набори
|
Степені |
Відповідний симетричний многочлен |
||
|
|
|
|
||
|
(4, 1, 0) |
3 |
1 |
0 |
|
|
(3, 2, 0) |
1 |
2 |
0 |
|
|
(3, 1, 1) |
2 |
0 |
1 |
|
|
(2, 2, 1) |
0 |
1 |
1 |
|
Тоді
існують такі числа
![]() та
та
![]() ,
що
,
що
![]()
![]() .
.
Задача зводиться до відшукання цих чисел.
Зауваження.
Оскільки
коефіцієнт при старшому одночлені
заданого многочлена дорівнює одиниці,
то і коефіцієнт при старшому доданку
![]() також дорівнює одиниці.
також дорівнює одиниці.
Підставляючи в ліву та праву частину набори значень аргументів, отримуємо систему відносно невідомих коефіцієнтів. Заповнимо наступну таблицю:
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
2 |
1 |
0 |
|
|
1 |
1 |
1 |
3 |
3 |
1 |
|
|
1 |
– 1 |
1 |
1 |
– 1 |
– 1 |
|
Розв’язуючи отриману систему
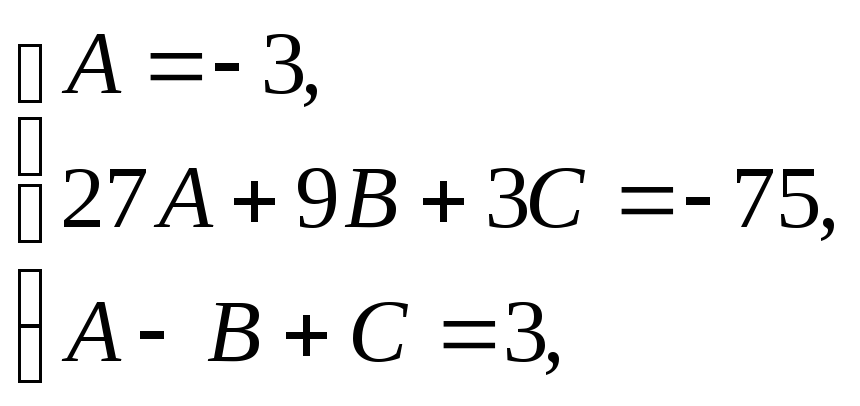
маємо,
що
![]() ,
,
![]() ,
,
![]() .
.
Таким
чином,
![]() .
.
Відповідь.
![]() .
.
5. Знайти значення виразу , де – корені многочлена .
Розв’язання.
! Теоретичні відомості !
Формули
Вієта.
Нехай задано многочлен
![]() .
Тоді якщо
.
Тоді якщо
![]() – це корені многочлена
– це корені многочлена
![]() ,
то
,
то
![]() ,
де
,
де
![]() – елементарні симетричні многочлени.
– елементарні симетричні многочлени.
Тобто коефіцієнти многочлена з точністю до знака виражаються як елементарні симетричні многочлени від його коренів. Вірне й обернене твердження.
Позначимо
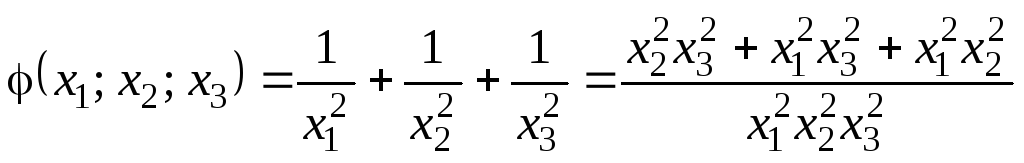 і запишемо даний симетричний многочлен
через елементарні симетричні поліноми.
Для многочлена
і запишемо даний симетричний многочлен
через елементарні симетричні поліноми.
Для многочлена
![]() одночлен, до якого змінна
одночлен, до якого змінна
![]() входить в максимальному степені, це
одночлен
входить в максимальному степені, це
одночлен
![]() .
Заповнюємо таблицю:
.
Заповнюємо таблицю:
|
Набори
|
Степені |
Відповідний симетричний многочлен |
||
|
|
|
|
||
|
(2, 2, 0) |
0 |
2 |
0 |
|
|
(2, 1, 1) |
1 |
0 |
1 |
|
Тоді
існує таке число
![]() ,
що
,
що
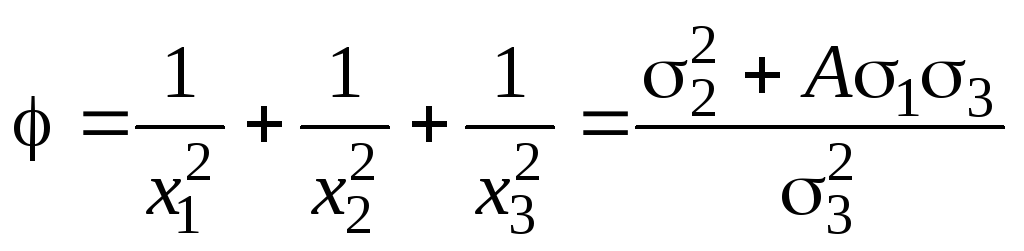 .
.
Знайдемо
значення величини
![]() .
.
Підставляючи в ліву та праву частину набори значень аргументів, отримуємо:
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
3 |
3 |
1 |
|
А
отже,
![]() .
Тобто
.
Тобто
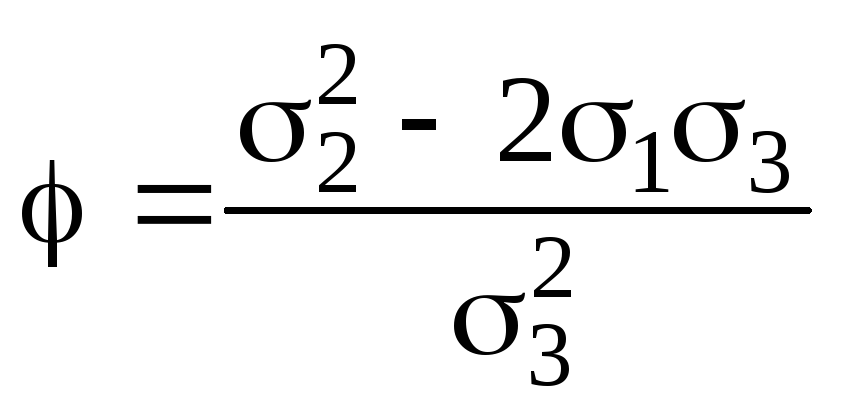 .
Тоді значення цього многочлена від
коренів многочлена
.
Тоді значення цього многочлена від
коренів многочлена
![]() :
:
 ,
,
![]() ,
,
![]() ,
,
![]() .
.
Тобто
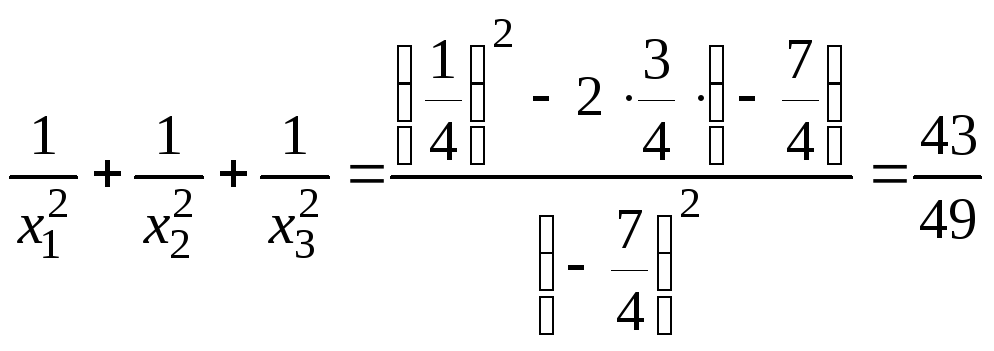
Відповідь.
![]() .
.
