5.1. Вычисление определителя. Общие положения

Одной из важных задач линейной алгебры является вычисление значения определителя квадратной матрицы. Можно привести, в частности, некоторые задачи, сопровождаемые вычислением определителей:

1) численные решение системы имеет смысл только в том случае, если определитель отличен от нуля;

2) если определитель мал по абсолютной величине, то вычисленные корни могут значительно отличаться от истинных;

3) при получении множественного коэффициента корреляции и частных коэффициентов корреляции необходимо неоднократно выполнять вычисление различных определителей, т.е. в этом случае вычисление определителей представляет и самостоятельный интерес.

Поэтому оказывается полезным сопровождение решения системы линейных уравнений вычислением определителя.

5.1.1. Вычисление определителя по методу Гаусса

Существуют различные методы вычисления определителя. Рассмотрим один из них, а именно основанный на изложенный выше метод Гаусса.

Обозначим определитель системы (4.1) через D. При приведении матрицы системы (4.1) к треугольному виду необходимо правую и левую части первого уравнения разделить на ведущий элемент . В этом случае определитель преобразованной системы будет . Последующие преобразования, связанные с исключением из остальных уравнений системы, величину определителя не изменяют.

На втором шаге, когда необходимо разделить обе части (преобразованного) второго уравнения на второй преобразованный элемент , определитель полученной системы будет . Операции по исключению из уравнений системы вновь не изменяют величину определителя.

На n- м шаге, осуществляя аналогичные действия, приходим к системе (4.1), определитель которой, очевидно, будет равен . Но матрица коэффициентов при неизвестных преобразованной системы – треугольная, с единицами по главной диагонали, поэтому ее определитель равен 1: = 1, следовательно,

(5.1)

Таким образом, значение определителя системы (4.1) получается как произведение ведущих элементов, используемых на каждом шаге.

5.1.2. Вычисление определителя по схеме Халецкого

Рассмотрим систему (4.2), обозначив

b = (5.2)

Представим матрицу А в виде произведения нижней треугольной матрицы В = и верхней треугольной матрицы С = с единичной диагональю:

А = ВС, (5.3)

т.е.

В = ; С = ,

где

(5.4)

(5.5)

Определитель матрицы А равняется

D = . (5.6)

Заметим, что система (4.2) по схеме Халецкого решается по следующей цепи уравнений:

By = b, Cx = y. (5.7)

Так как матрицы В и С – треугольные, искомые величины, можно вычислить по следующим формулам:

(5.8)

(5.9)

Пример вычисления по схеме Халецкого дан в Методических указаниях.

5.3. Вычисление обратной матрицы

Задачу вычисления обратной матрицы рассмотрим на примере квадратной матрицы размерности . В выражении (4.3) обозначим матрицу, обратную А, через W, т.е. в (4.3) полагаем = , и раскроем выражение = E (учитывая определение единичной матрицы) в таком виде:

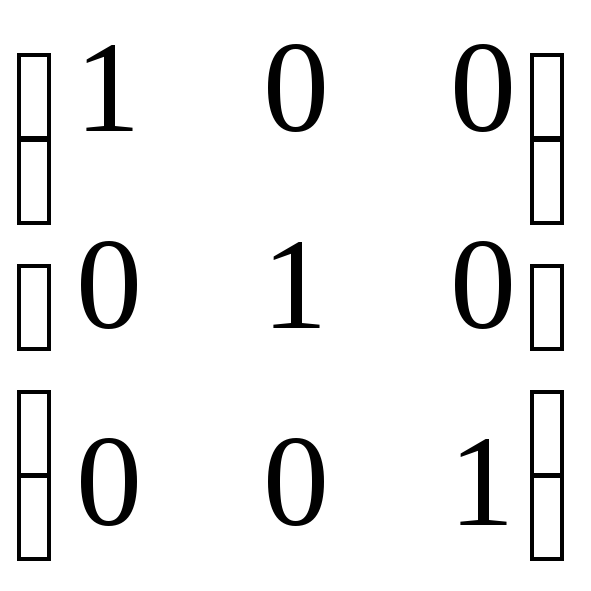= . (5.10)

Легко проверить что выражение (5.10) есть запись следующих трех систем линейных уравнений относительно неизвестных элементов W:

,

,

;

,

, (5.11)

;

,

,

,

Последовательно решая эти системы (например, методом Гаусса), поочередно вычисляем элементы столбцов обратной матрицы W.

Данную схему вычисления элементов обратной матрицы можно распространить и для случая, когда исходная матрица А имеет размерность .