Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский государственный энергетический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3_Lek.doc

Скачиваний:

Добавлен:

20.12.2018

Размер:

801.79 Кб

Скачать

☆

1 / 61 2 3 4 5 6 > Следующая >>>

Численные методы

ЛЕКЦИЯ 3

ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ

ЛЕКЦИЯ 3

Тема. Решение систем линейных уравнений.

2.1. Общие положения. Определения. Понятия

Пусть дана система линейных уравнений с неизвестными:

(4.1)

Систему (4.1) можно записать в векторно-матричной форме:

, (4.2)

где:

= ; = ; =

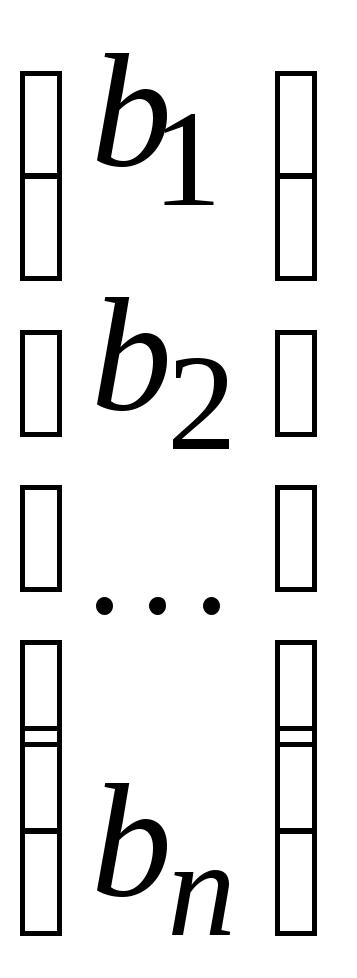
( – квадратная матрица, содержащая строк и столбцов, и – заданный и искомый -компонентные векторы).

Решением системы линейных уравнений называется такая совокупность чисел (значений неизвестных), которые при подстановке в каждое уравнение системы вместо соответствующих неизвестных обращают его в тождество.

Система, для которой существует хоть одно решение, называется совместной.

Совместная система, имеющая единственное решение, называется определенной, совместная же система, имеющая сколько угодно решений, называется неопределенной, а система, не имеющая ни одного решения, называется несовместной.

Единичной называется матрица E, у которой диагональные элементы равны единице, недиагональные – нулю.

Обратной по отношению к данной называется матрица , которая будучи умноженной как справа, так и слева на указанную матрицу, дает единичную матрицу, т.е.

А = А = Е. (4.3)

Если к матрице А добавить столбец свободных членов, получим присоединенную матрицу В:

B = .

Транспонированная матрица получается перестановкой в матрице А строк со столбцами.

Матрица Т трехдиагональная, если у нее все элементы, не лежащие на трех центральных сопряженных диагоналях, равны нулю.

= ; (4.4)

Z = . (4.5)

Если квадратная матрица А равна транспонированной (А = ), т.е. , то матрица А называется симметричной.

Треугольной называется матрица, у которой все лежащие ниже (или выше) диагональной элементы равны нулю.

Матрица называется ортогональной, если сумма квадратов элементов каждого столбца равна единице, а сумма произведений соответствующих элементов двух различных столбцов равна нулю, т.е. А = Е

Предположим, что система (2.1) не вырождена, т.е. ее определитель отличен от нуля: (другими словами, матрица А – неособенная). В этом случае она имеет единственное решение, которое можно получить, применяя различные методы.

Многообразие численных методов решения систем линейных уравнений можно разделить на прямые (точные) и итерационные (приближенные).

Прямыми называются методы, которые позволяют за конечное число арифметический операций получить точное решение системы (например, метод Крамера, метод Гаусса и его модификации и другие. Итерационные методы дают приближенное решение системы с заданной точностью. Точное решение теоретически может быть получено как результат бесконечного единообразного процесса. К итерационным методам относятся: метод простой итерации, метод Зейделя, градиентные методы и их модификации.

4.2. Метод Гаусса

Метод Гаусса основан на приведении матрицы системы к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений системы.

Сначала с помощью первого уравнения исключается из второго и всех последующих уравнений системы. Затем с помощью второго уравнения исключается из третьего и всех последующих уравнений. Этот процесс продолжается до тех пор, пока в левой части последнего (n-го) уравнения не останется лишь один член с неизвестным , т. е. матрица системы будет приведена к треугольному виду. Этот процесс называется прямым ходом метода Гаусса.

Обратный ход метода Гаусса состоит в последовательном вычислении искомых неизвестных: решая последнее уравнение, находим ; далее, используя это значение, из предпоследнего уравнения вычисляем и т.д. Последним будет найден из первого уравнения.

Проиллюстрируем метод Гаусса на примере решения системы из трех линейных уравнений; в этом случае (то есть для n = 3) система (2.1) запишется в следующем виде:

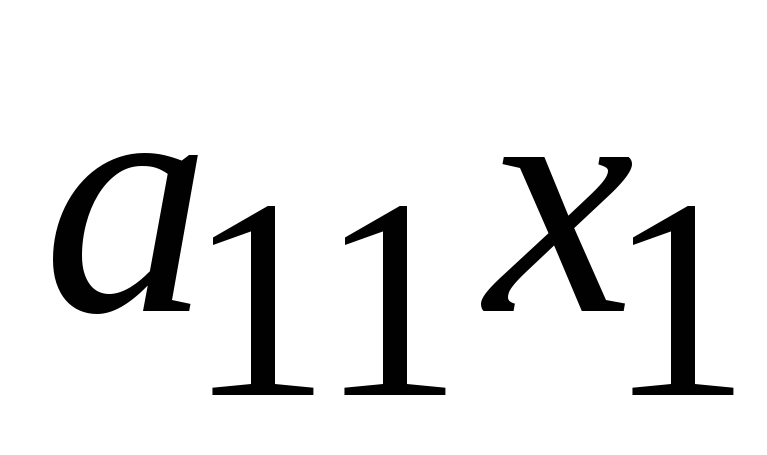
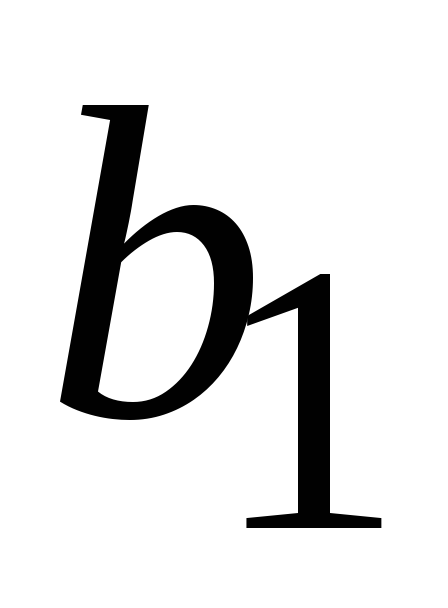+	+	=	,	(4.6)
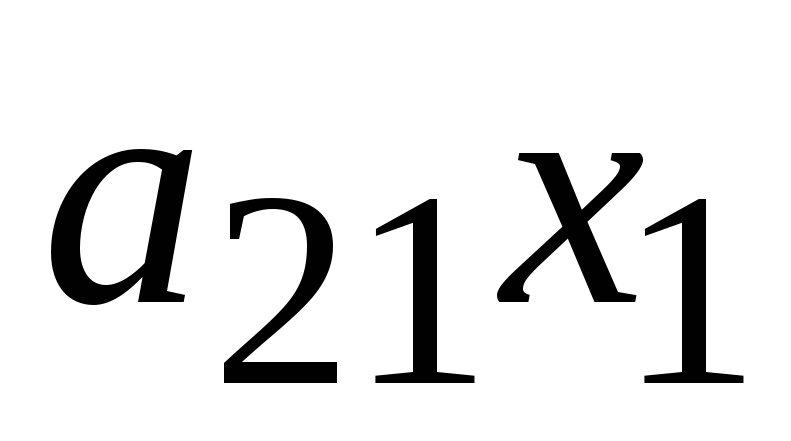
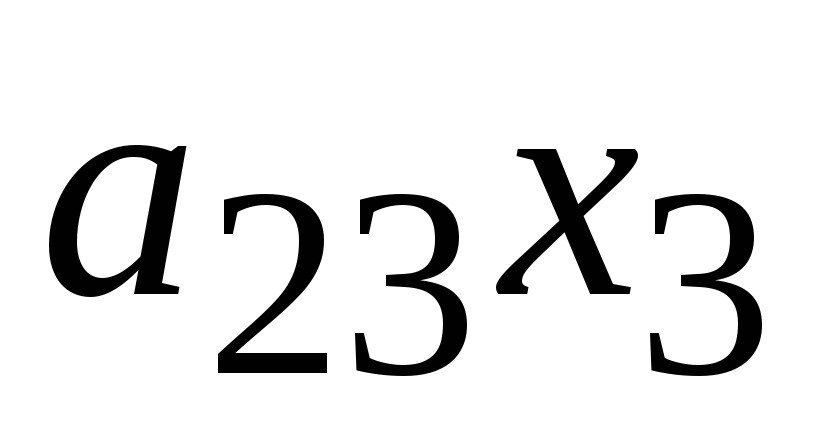
+	+	=	,	(4.7)
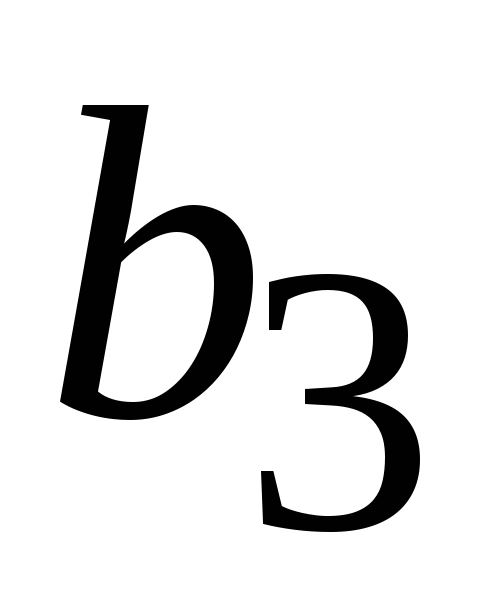+	+	=	.	(4.8)

Предполагается, что . Если это не так, необходимо переставить уравнения (4.6) – (4.8) таким образом, чтобы в первом уравнении коэффициент при не был равен нулю.

Решение будем выполнять поэтапно, обозначая каждый этап через k .

k = 1

i = 2. Определим множитель для уравнения (2.7).

Умножим первое уравнение, т.е. (4.6), на множитель и вычтем из второго:

. (4.9)

Используя обозначения , и и учитывая, что в уравнении (4.7) коэффициент при равен нулю (так как, подставляя выражение для c, получаем ) уравнение (4.7) запишется в следующем виде:

i = 3. Определим множитель и выполним ту же самую процедуру для третьего уравнения (4.8) c использованием соответствующих обозначений, тогда искомая система (4.6) – (4.8) примет следующий вид:

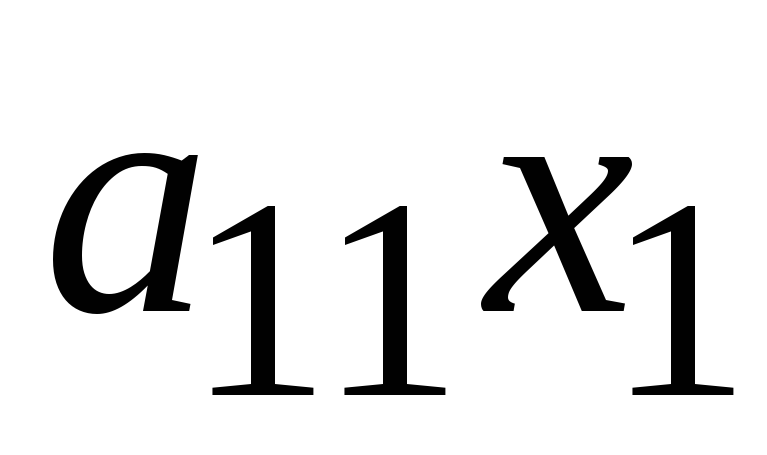
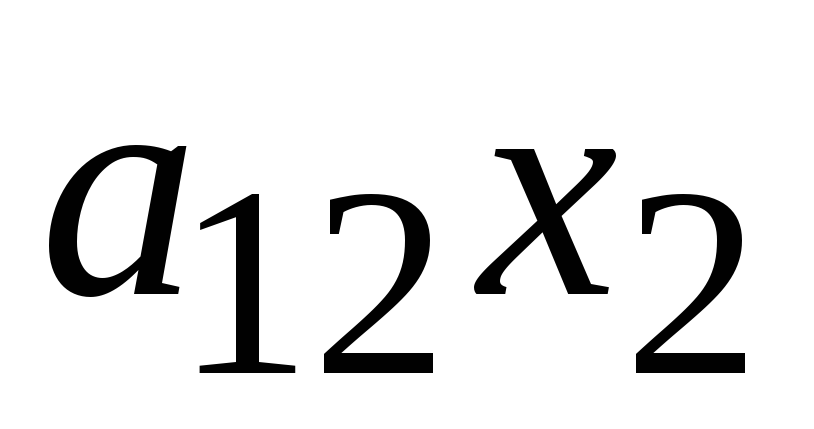
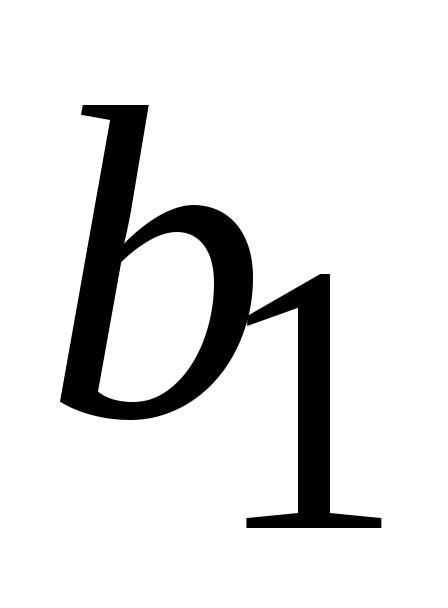	+	+	=	,	(2.2, а)
0	+	+	=	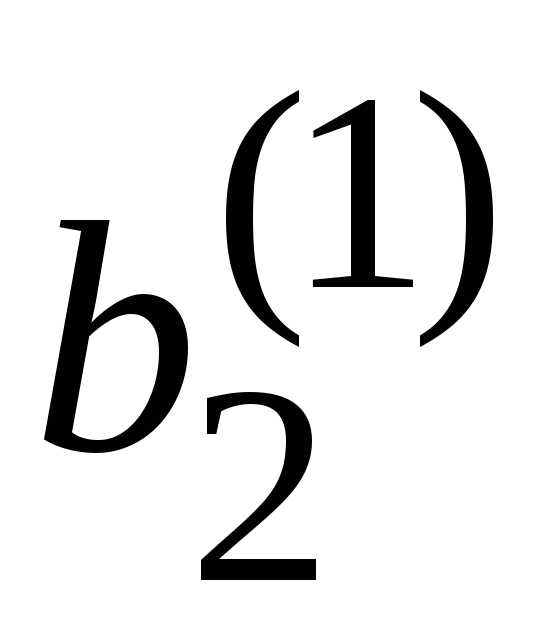,	(2.3, а)
0	+	+	=	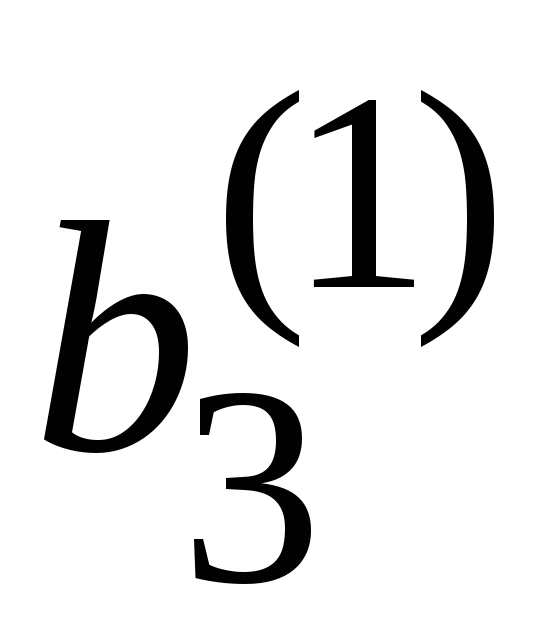.	(2.4, а)

Как видим, остается преобразовать последнее уравнение в системе (2.2, а) – (2.4, б) для приведения системы к треугольному виду; поэтому переходим к следующему этапу.

k = 2

i = 3. По схеме, аналогичной для случая k = 2, вводим множитель , умножаем второе уравнение (2.2, а) на множитель и вычитаем из третьего и, используя соответствующие обозначения и учитывая, что коэффициент при в третьем уравнении равен нулю (ср. с (2.2, а ) и (2.3,а)), получаем окончательно треугольную матрицу для нашей системы:

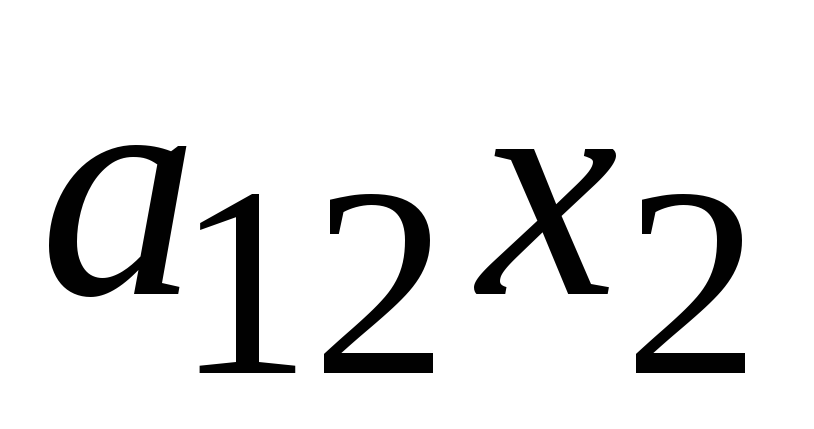
	+		+	=	,	(4.10)
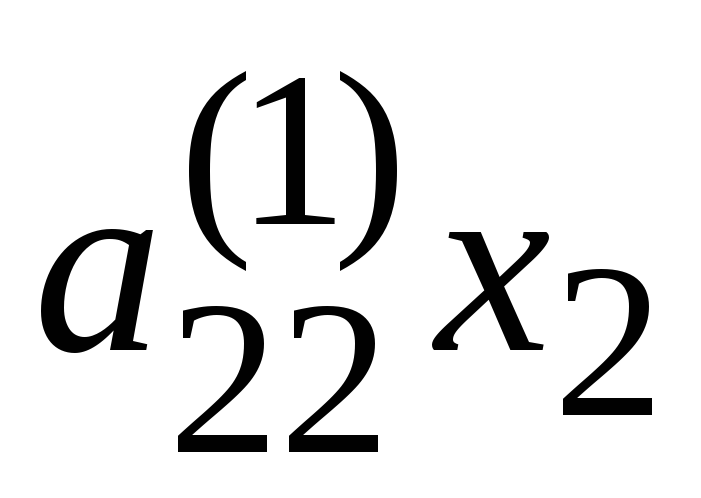
0	+		+	=	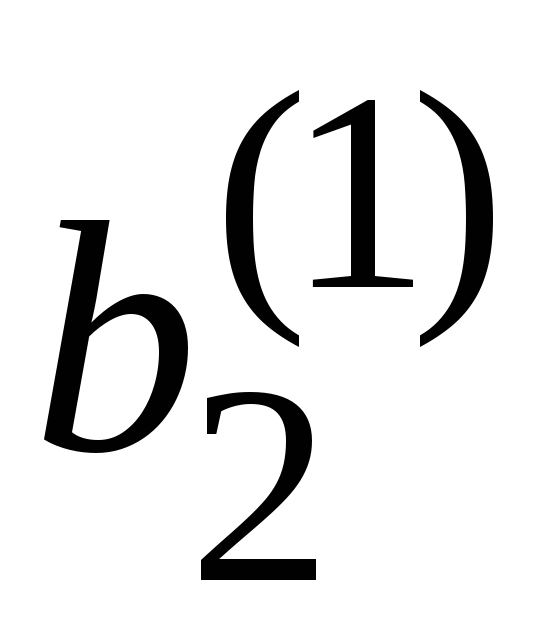,	(4.11)
0	+	0	+	=	.	(4.12)

где , .

Для системы (4.10) – (4.12), выполняют обратный ход, т.е находят сначала из уравнения (4.12) и затем, подставляя его в (4.11), находят ; аналогично определяют :