4.3 Метод прогонки

Пусть имеется разреженная система с трехдиагональной матрицей, т.е. ненулевые элементы находятся лишь на главной и двух соседней с ней диагоналях, расположенных сверху и снизу (см.(4.5)):

+ + = , (4.21)

i = 1, 2, …, n; = 0, =0, = 0, =0, 0, (4.22)

тогда данная система, , например из пяти уравненй (n = 5), запишется так:

+					=,
+	+				=,
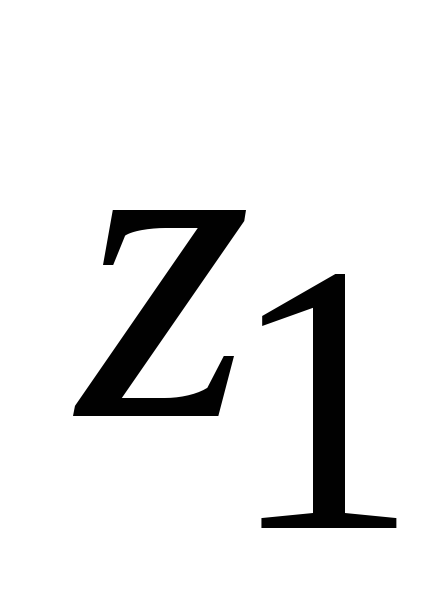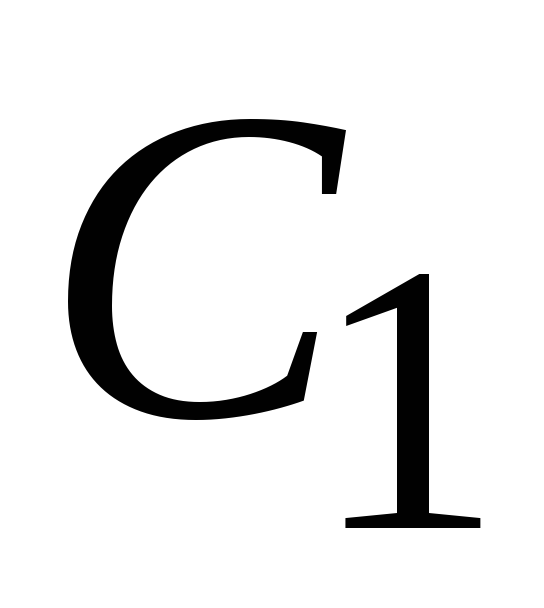
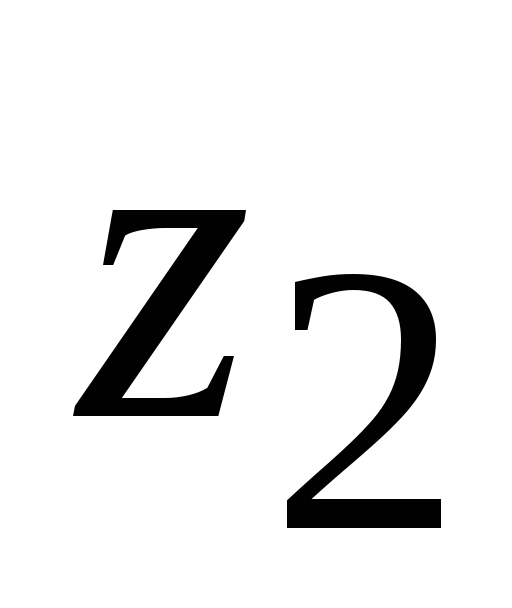
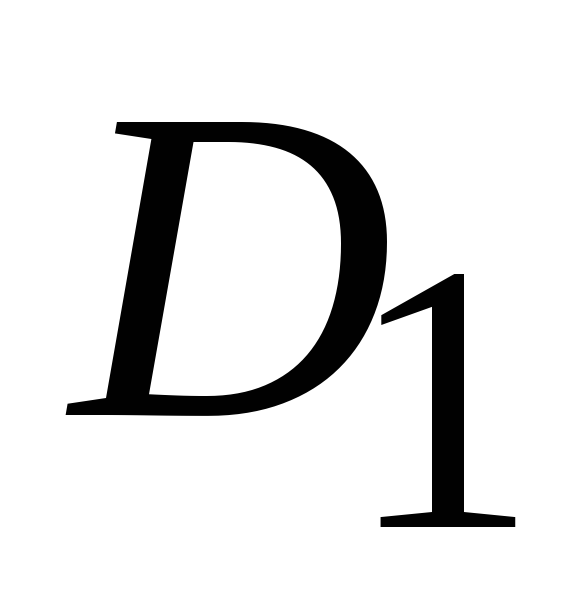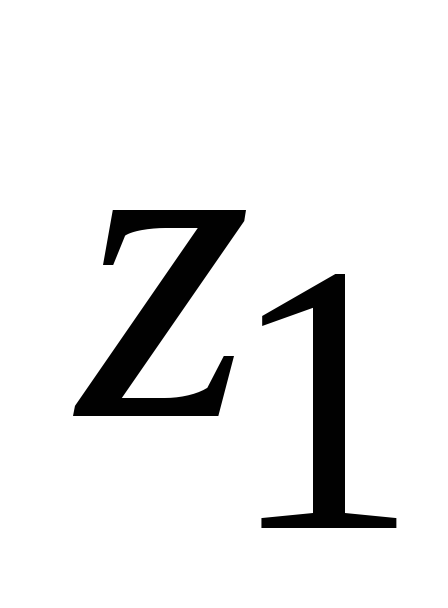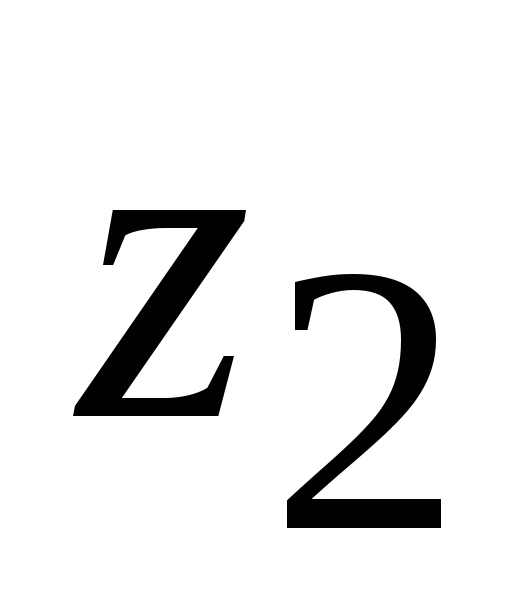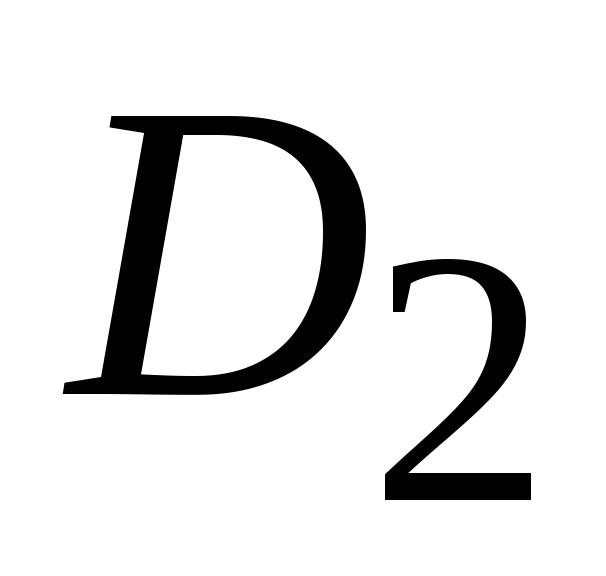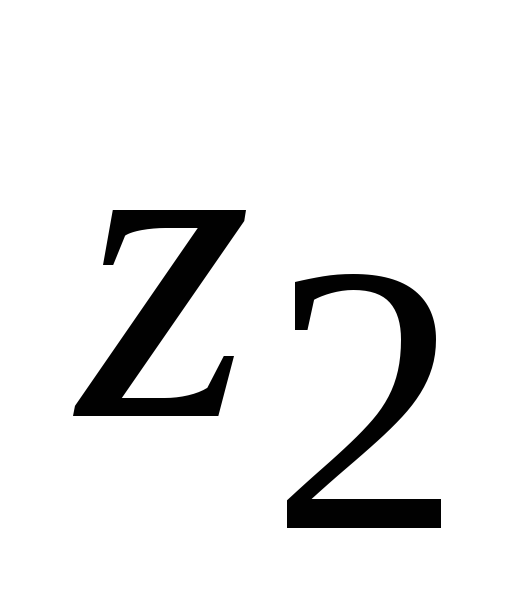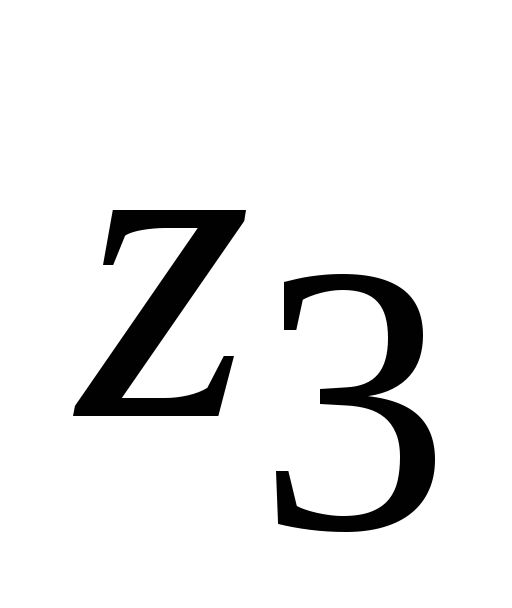	+	+			=, (4.23)
		+	+		=,
			+		=.

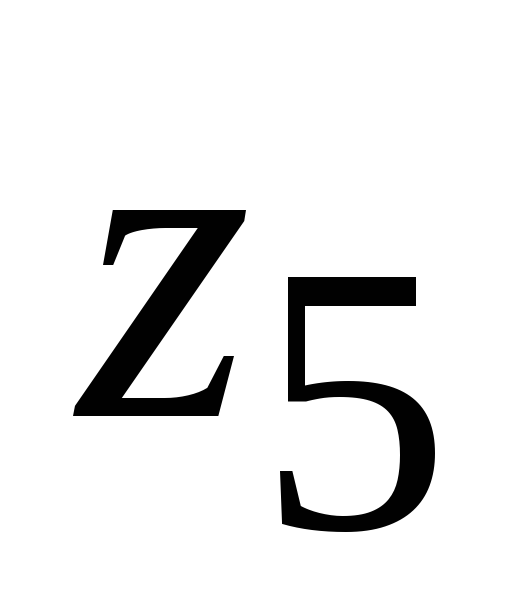
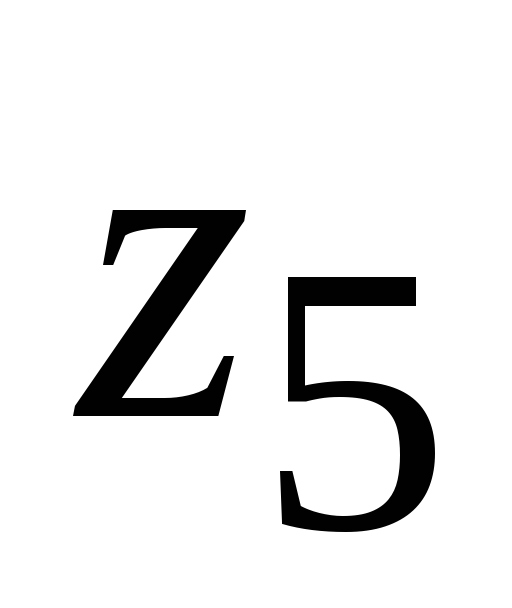
Замечание. В дальнейшем, при выводе рабочих формул, ссылку будем делать в основном на систему (4.23), предполагая, что последнее (пятое) уравнение имеет порядковый номер п.

Такие системы получаются при моделировании некоторых инженерных задач, а также при численном решении краевых задач для дифференциальных уравнений. Для решения системы (4.21) – (4.22) обычно применяется метод прогонки, который является частным случаем метода Гаусса, и состоит из двух этапов – прямой прогонки (аналог прямого хода) и обратной прогонки (аналог обратного хода метода Гаусса).

Прямая прогонка состоит в том, что каждое неизвестное выражается через с помощью прогоночных коэффициентов и :

= + , i = 1, 2, …, n – 1. (4.24)

Коэффициенты и вычисляются следующим образом.

Первое уравнение системы (4.23) разрешим относительно , а уравнение (4.21) запишем для i = 1:

=(–/)+ (/),

= + . (4.25)

Приравнивая коэффициенты при неизвестных и , получаем:

= –/, = /. (4.26)

Второе уравнение системы (4.23) запишем, заменяя по формуле (4.25):

(+ ) + + = .

Отсюда находим:

= [–/(+)]+ (–)/(+)

Но, с другой стороны (см. (4.24)),

= + .

Сравнивая последнее уравнение с предшествующим, определяем:

= –/(+), = (–)/(+).

То есть, формулы для вычисления и (i = 2, 3,…, n – 1) будут следующие:

= , = , (4.27)

Таким образом, в результате выполнения первого этапа (проведения прямой прогонки), последовательно применяя формулы (4.26) и (4.27), вычисляем все значения и (i = 1, 2, …, n – 1).

Обратная прогонка заключается в последовательном вычислении неизвестных . С этой целью сначала нужно найти . Если воспользоваться выражениями (4.24) при i = n – 1 и последним уравнением системы (4.23) (учитывая замечание к этой системе), получим:

= +,

+ = .

Исключая из последних двух выражений, находим

= . (4.28)

Далее, используя вычисленные значения и , по формуле (4.24) последовательно вычисляем , , …, .

Метод прогонки из-за его устойчивости можно применять для решения больших систем уравнений.