3.1. Метод Ньютона для системы нелинейных уравнений.

Рассмотрим метод Ньютона для системы, состоящей из n нелинейных уравнений.

Пусть дана система нелинейных уравнений

(3.1)

с действительными левыми частями.

Систему (3.1) можно записать короче. Для этого введем следующие обозначения:

; ,

т. е. совокупность аргументов , , …, и совокупность функций , , …, представим как n-мерные векторы (f называют вектор-функцией)

Тогда система (3.1) с этими обозначениями кратко запишется так:

(3.2)

Систему (3.2) решают методом последовательных приближений.

Пусть  точное значение корня. В методе Ньютона последовательные приближения точного корня вырабатываются по следующей формуле (даем без доказательства ):

(p = 0, 1, 2, …, n), (3.3)

где есть матрица Якоби системы функций , , …, относительно переменных , , …, , причем предполагается, что матрица  неособенная (определитель отличен от нуля, что является и необходимым условием сходимости итерационного процесса(3.3)), поэтому существует ее обратная матрица ; таким образом, можно записать:

.

Заметим, для применеия метода Ньютона требуется хорошее отделения корня.

На практике применением достаточного условия сходимости из-за его громозкости предпочитают, как правило, не воспользоваться.

Вычислительный процесс (3.3) продолжают до тех пор, пока не выполнится условие

,

где – заданноя точность вычисления. При достижении этого условия за решение системы (3.1) принимается .

За нулевое приближение можно взять грубое значение искомого корня.

Как видно из формулы (3.3), при нахождении корня по этой формуле необходимо составить обратную матрицу . В общем случае, для этого используют численные методы, в частности метод Гаусса для решения систем линейных уравнений. Здесь мы напомним, как составляется обратная матрица в случае, когда порядок исходной матрицы невысокий.

Пусть дана неособенная матрица n-го порядка

, (3.4)

где .

Для матрицы A составляем так называемую присоединенную (или союзную) матрицу

, (3.5)

где  алгебраические дополнения соответствующих элементов (i, j = 1, 2, …, n). Напоминаем, алгебраические дополнения вычисляются по формуле , где  минор основного определителя n-го порядка (как известно, минор элемента вычисляется так: если в (3.4) вычеркнуть i-ю строку и j-й столбец, на пересечении которых находится элемент , то останется (n  1) строк и столбцов; определитель матрицы, полученной таким образом и есть минор ).

В частности, на примере определителя третьего порядка

покажем, как вычисляются значения . Например:

= , (3.6)

= , (3.7)

= (3.8)

и т. д.

Необходимо обратить на следующее: алгебраические дополнения элементов строк помещаются в соответствующих столбцах, т. е. выполняется операция транспонирования.

Для составления обратной матрицы разделим элементы матрицы на определитель матрицы

. (3.9)

Пример 3.1. Методом Ньютона приближенно найти положительное решение системы уравнений

исходя из начального приближения

.

Решение. Имеем

.

Подставляя начальные данные, получаем

= . (3.10)

Составим матрицу Якоби

. (3.12)

Подстановкой начальных значений в (3.12) получаем

(3.13)

и

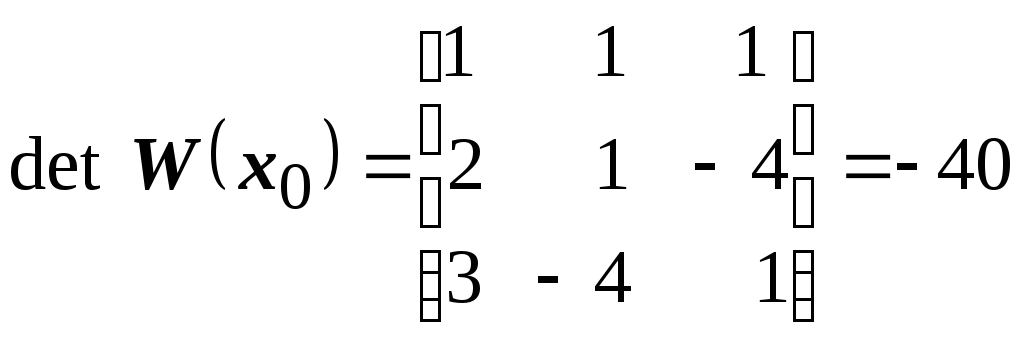. (3.14)

Далее, для вычисления обратной матрицы вычисляем алгебраические дополнения. Например (используя (3.6) – (3.8) с нашими обозначениями):

.

Аналогично можно получить остальные значения. В итоге получим обратную матрицу в следующем виде:

= . (3.15)

По формуле (3.3) получаем первое приближение

=  =

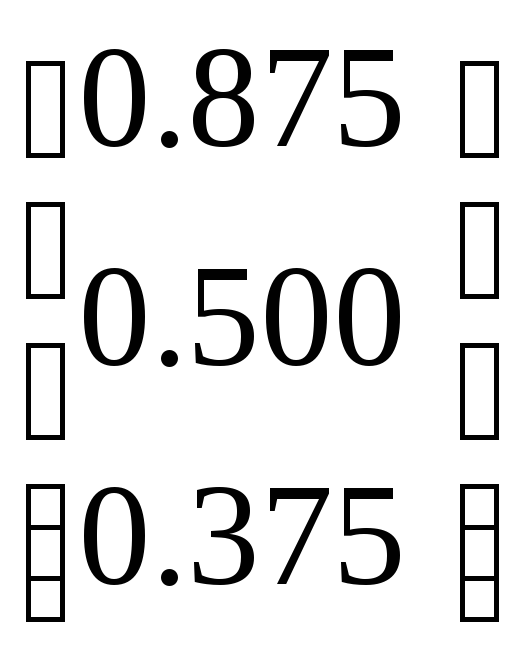= + = . (3.16)

Таким образом, получаем следующие значения корней при первом приближении: , и . Затем, повторяя этапы (3.13)-(3.16), находим последующие приближения. Например, для второго и третьего приближений соответственно определяем

, .

Рассмотрим метод Ньютона для системы двух уравнений.

Пусть ,  приближенные корни системы нелинейных уравнений

; , (3.17)

где F и G  непрерывно дифференцируемые функции. Полагая

; , (3.18)

получим следующую систему:

(3.19)

Из системы (3.19), используя формулу Тейлора и ограничиваясь линейными членами относительно и , будем иметь:

(3.20)

Если якобиан

,

то из системы (3.20) можно найти

, (3.21)

. (3.22)

Тогда, учитывая (3.18), можно записать:

, (3.23)

(3.24)

(n = 0, 1, 2, …).

Начальные приближения , определяются грубо приближенно, например, графическим путем.

Пример вычисления корней системы двух нелинейных уравнений дан в Методических указаниях.