- •Министерство образования и науки российской федерации
- •Кумертауский филиал
- •Двоично-шестнадцатеричная таблица
- •Двоично-восьмеричная таблица
- •Лабораторная работа № 1 "Связывание и внедрение объектов"
- •Методические указания.
- •Методические указания.
- •Методические указания.
- •Методические указания.
- •Контрольные вопросы.
- •Литература:
- •Лабораторная работа № 2
- •Вопросы при сдаче лабораторной работы:
- •Лабораторная работа № 3
- •Задание
- •Лабораторная работа № 4
- •Вопросы при сдаче лабораторной работы:
- •Лабораторная работа № 5
- •Вопросы при сдаче лабораторной работы:
- •Лабораторная работа №6
- •2) Исследуйте способы активизации четырех окон Delphi:
- •9)Выполните программу еще раз.
- •Лабораторная работа №7
- •Лабораторная работа №8
- •Лабораторная работа №9-10
- •Лабораторная работа №11-12
- •Изменить заголовок формы с «Form1» на «Биржа ценных бумаг» и увеличить размеры формы.
- •Откажитесь от возможности изменять размеры окна программы, присвоив свойству формы BorderStyle значение bsDialog.
- •Сохраните созданную в данный момент форму в своей папке.
- •Расположите в нижней части формы две пиктографические кнопки типа SpeedButton и кнопку окончания работы программы BitBtn (см. Рис1).Задайте следующие значения свойств вставленных объектов:
- •Вставьте в форму три таблицы текстовых строк StringGrid (см. Рис1).Задайте следующие значения свойств этих объектов:
- •Разместите на форме текстовые поля так, как показано на рис.1.
- •В окне текста программы перед разделом implementation введите описание констант и переменных программы:
- •Запрограммируйте кнопки SpeedButton1 и SpeedButton2 так:
- •Сохраните выполненную на данный момент программу в своей папке.
- •Запустите созданную программу и проследите за её работой.
- •Создайте ехе-файл программы.
- •Продемонстрируйте созданную программу преподавателю. Закончите работу.
Министерство образования и науки российской федерации
Федеральное агентство по образованию
Кумертауский филиал
государственного образовательного учреждения
высшего профессионального образования
«Оренбургский государственный университет»
Кафедра общих математических и естественнонаучных дисциплин
|
|
Утверждаю Директор
_____________________В.А. Анищенко подпись «____»_________________200… г
|
Руководство по проведению
лабораторно-практических работ
по дисциплине
«Информатика»
Направление подготовки: 080100 «Экономика и управление»
Специальность: 080100 – «Экономика»
Специализация: 080100.62 – «Бакалавр экономики»
Форма обучения: очная
Кумертау 2011г.
Перечень практических работ по дисциплине
«Информатика».
1 семестр
Практическая работа № 1
Тема: Измерение информации.
Практическая работа № 2
Тема: Системы счисления.
Практическая работа № 3
Тема: Кодирование текстовой и графической информации.
 Практическая
работа №
1.
Практическая
работа №
1.
Тема: Измерение информации.
Цель работы: изучить основные способы измерения информации и освоить формулы Хартли и Шеннона для измерения количества информации, получаемой в процессе сообщения.
Оборудование: ПК.
Место проведения: аудитория _1205___
Порядок выполнения работы.
Задачи
-
Априори известно, что шарик находится в одной из трех урн: А, В или С. Определите, сколько бит информации содержит сообщение о том, что он находится в урне В. Варианты: 1 бит, 1,58 бита, 2 бита, 2,25 бита.
-
Вероятность первого события составляет 0,5, а второго и третьего 0,25. Чему для такого распределения равна информационная энтропия. Варианты: 0,5 бита, 1 бит, 1,5 бита, 2 бита, 2,5 бита, 3 бита.
-
Вот список сотрудников некоторой организации:
-
Год рождения
Фамилия
Имя
1970
Иванова
Марина
1970
Иванова
Наталья
1970
Петрова
Татьяна
1970
Звягина
Ирина
Определите количество информации, недостающее для того, чтобы выполнить следующие просьбы:
-
Пожалуйста, позовите к телефону Иванову.
-
Меня интересует одна ваша сотрудница, она 1970 года рождения.
-
Какое из сообщений несет больше информации:
В результате подбрасывания монеты (орел, решка) выпала решка.
На светофоре (красный, желтый, зеленый) сейчас горит зеленый свет.
В результате подбрасывания игральной кости (1, 2, 3, 4, 5, 6) выпало 3 очка.
Контрольные вопросы:
-
Что такое информация и информатика?
-
Какие основные свойства имеет информация?
Литература:
-
Информатика. Базовый курс. Под ред. Симановича С.В. – СПб: «Питер», 2003.
-
Могилев А.В. , Пак Н.И. , Хеннер Е.К. Информатика: Учеб. Пособие для студ. / Под ред. Е.К.Хеннера. – М.: «Академия» , 2001.
-
В.Э. Фигурнов «IBM PC для пользователя»

 Практическая
работа №
2.
Практическая
работа №
2.
Тема: Системы счисления.
Цель работы: изучить способы представления числовой информации с помощью систем счисления.
Оборудование: ПК.
Место проведения: аудитория _1205___
Порядок выполнения работы.
Перевод чисел из одной системы счисления в другую
![]() Наиболее
часто встречающиеся системы счисления
-- это двоичная, шестнадцатеричная и
десятичная. Как же связаны между собой
представления числа в различных системах
счисления? Рассмотрим различные способы
перевода чисел из одной системы счисления
в другую на конкретных примерах.
Наиболее
часто встречающиеся системы счисления
-- это двоичная, шестнадцатеричная и
десятичная. Как же связаны между собой
представления числа в различных системах
счисления? Рассмотрим различные способы
перевода чисел из одной системы счисления
в другую на конкретных примерах.
Пусть требуется перевести число 567 из десятичной в двоичную систему. Сначала определим максимальную степень двойки, такую, чтобы два в этой степени было меньше или равно исходному числу. В нашем случае это 9, т. к. 29=512, а 210=1024, что больше начального числа. Таким образом, мы получим число разрядов результата. Оно равно 9+1=10. Поэтому результат будет иметь вид 1ххххххххх, где вместо х могут стоять любые двоичные цифры. Найдем вторую цифру результата. Возведем двойку в степень 9 и вычтем из исходного числа: 567-29=55. Остаток сравним с числом 28=256. Так как 55 меньше 256, то девятый разряд будет нулем, т. е. результат примет вид 10хххххххх. Рассмотрим восьмой разряд. Так как 27=128>55, то и он будет нулевым.
Седьмой разряд также оказывается нулевым. Искомая двоичная запись числа принимает вид 1000хххххх. 25=32<55, поэтому шестой разряд равен 1 (результат 10001ххххх). Для остатка 55-32=23 справедливо неравенство 24=16<23, что означает равенство единице пятого разряда. Действуя аналогично, получаем в результате число 1000110111. Мы разложили данное число по степеням двойки:
567=1*29+0*28+0*27+0*26+1*25+1*24+0*23+1*22 +1*21+1*20
При другом способом перевода чисел используется операция деления в столбик. Рассмотрим то же самое число 567. Разделив его на 2, получим частное 283 и остаток 1. Проведем ту же самую операцию с числом 283. Получим частное 141, остаток 1. Опять делим полученное частное на 2, и так до тех пор, пока частное не станет меньше делителя. Теперь для того, чтобы получить число в двоичной системе счисления, достаточно записать последнее частное, то есть 1, и приписать к нему в обратном порядке все полученные в процессе деления остатки.
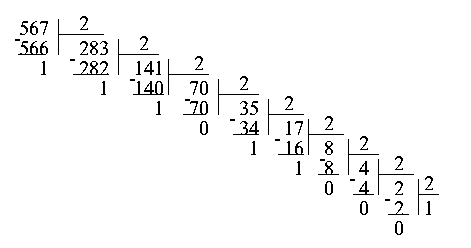
 Результат,
естественно, не изменился: 567 в двоичной
системе счисления записывается как
1000110111.
Результат,
естественно, не изменился: 567 в двоичной
системе счисления записывается как
1000110111.
Эти два способа применимы при переводе числа из десятичной системы в систему с любым основанием. Для закрепления навыков рассмотрим перевод числа 567 в систему счисления с основанием 16.
Сначала осуществим разложение данного числа по степеням основания. Искомое число будет состоять из трех цифр, т. к. 162=256 < 567 < 163=4096. Определим цифру старшего разряда. 2*162=512<567<3*162=768, следовательно искомое число имеет вид 2хх, где вместо х могут стоять любые шестнадцатеричные цифры. Остается распределить по следующим разрядам число 55 (567-512). 3*16=48<55<4*16=64, значит во втором разряде находится цифра 3. Последняя цифра равна 7 (55-48). Искомое шестнадцатеричное число равно 237.
Второй способ состоит в осуществлении последовательного деления в столбик, с единственным отличием в том, что делить надо не на 2, а на 16, и процесс деления заканчивается, когда частное становится строго меньше 16.
|
Конечно, не надо забывать и о том, что для записи числа в шестнадцатеричной системе счисления, необходимо заменить 10 на A, 11 на B и так далее. |
|
Операция перевода в десятичную систему выглядит гораздо проще, так как любое десятичное число можно представить в виде x = a0*pn + a1*pn-1 + ... + an-1*p1 + an*p0, где a0 ... an -- это цифры данного числа в системе счисления с основанием p.
Пример Переведем число 4A3F в десятичную систему. По определению, 4A3F= 4*163+A*162+3*16+F. Заменив A на 10, а F на 15, получим 4*163+10*162+3*16+15= 19007.
Пожалуй, проще всего осуществляется перевод чисел из двоичной системы в системы с основанием, равным степеням двойки (8 и 16), и наоборот. Для того чтобы целое двоичное число записать в системе счисления с основанием 2n, нужно
-
данное двоичное число разбить справа налево на группы по n-цифр в каждой;
-
если в последней левой группе окажется меньше n разрядов, то дополнить ее нулями до нужного числа разрядов;
-
рассмотреть каждую группу, как n-разрядное двоичное число, и заменить ее соответствующей цифрой в системе счисления с основанием 2n.