
- •1. Были сгенерированы две повторные выборки по 100 элементов.
- •2. Найти выборочное среднее и дисперсию, экстремальные значения, размах, выборочную медиану.
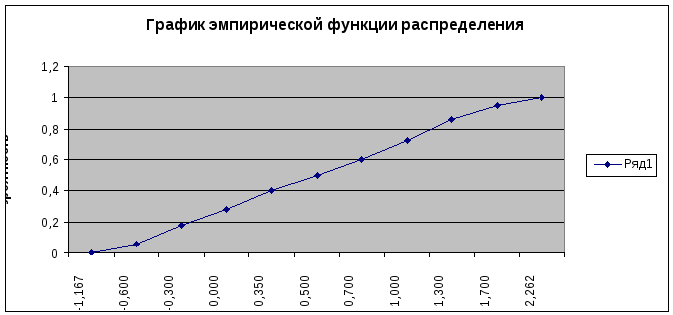
- •3. Построить график эмпирической функции распределения и гистограмму. Сгладить гистограмму с помощью нормальной плотности, оценив предварительно параметры.
- •5. Построим оценки параметров для нормального распределения по методу наибольшего правдоподобия.
- •6. Доверительный интервал.
- •7. По критерию проверим согласие эмпирических данных с нормальным распределением
- •8. Проверка выполнения критерия однородности для объединения двух выборок.
- •9. Проверка гипотезы о параметрах нормального распределения.
- •10. Проверка гипотезы о равенстве средних.
2. Найти выборочное среднее и дисперсию, экстремальные значения, размах, выборочную медиану.
Пусть
![]() – первая повторная выборка.
– первая повторная выборка.
Выборочным
средним
является число
![]() =
0,512972,
выборочной
дисперсией
–
=
0,512972,
выборочной
дисперсией
–
![]() =
0,542224,
минимумом
=
0,542224,
минимумом
![]() -1,16748,
максимумом
– 2,262448,
размахом
3,42993,
выборочной
медианой
-0,502996.
-1,16748,
максимумом
– 2,262448,
размахом
3,42993,
выборочной
медианой
-0,502996.
3. Построить график эмпирической функции распределения и гистограмму. Сгладить гистограмму с помощью нормальной плотности, оценив предварительно параметры.
 число
элементов выборки Х меньших y,
N=100.
число
элементов выборки Х меньших y,
N=100.
Границы интервалов:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
-1,167 |
-0,600 |
-0,300 |
0,000 |
0,350 |
0,500 |
0,700 |
1,000 |
1,300 |
1,700 |
2,262 |
Интервалы и данные для построения гистограммы:
|
|
a0-a1 |
a1-a2 |
a2-a3 |
a3-a4 |
a4-a5 |
a5-a6 |
a6-a7 |
a7-a8 |
a8-a9 |
a9-a10 |
|
n |
6 |
12 |
10 |
12 |
10 |
10 |
13 |
13 |
9 |
5 |
|
h |
0,1057 |
0,4000 |
0,3333 |
0,3429 |
0,6667 |
0,5000 |
0,4333 |
0,4333 |
0,2250 |
0,0889 |
|
y |
-0,8837 |
-0,4500 |
-0,1500 |
0,1750 |
0,4250 |
0,6000 |
0,8500 |
1,1500 |
1,5000 |
1,9812 |
|
y* |
-2,5759 |
-1,7760 |
-1,2227 |
-0,6233 |
-0,1622 |
0,1605 |
0,6216 |
1,1748 |
1,8203 |
2,7078 |
|
fi(y*) |
0,0145 |
0,0824 |
0,1889 |
0,3285 |
0,3937 |
0,3938 |
0,3289 |
0,2001 |
0,0761 |
0,0102 |
|
fi(y*)/S |
0,0267 |
0,1520 |
0,3484 |
0,6059 |
0,7261 |
0,7263 |
0,6065 |
0,3690 |
0,1403 |
0,0188 |

5. Построим оценки параметров для нормального распределения по методу наибольшего правдоподобия.
 ;
;
![]() -
параметры;
-
параметры;
Пусть
![]() -
повторная выборка.
-
повторная выборка.

 …
… .
.
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
Следовательно
![]()
6. Доверительный интервал.
1)
доверительный интервал уровня
![]() для а строится по правилу(
для а строится по правилу(
![]() известно
) :
известно
) :
![]() ,
,
Где
константа
![]() определяется по таблицам нормального
распределения из соотношения 2
определяется по таблицам нормального
распределения из соотношения 2![]()
2)
доверительный интервал уровня
![]() для а строится по правилу(
для а строится по правилу(
![]() не известно )
не известно )
![]()
![]() 1,660391156;
1,660391156;
![]() 0,542224;
0,542224;
3)
доверительный
интервал уровня
![]() для
для
![]() строится по правилу:
строится по правилу:
![]()
Где
константы
![]() и
и
![]() находим из таблиц
находим из таблиц
![]() распределения с N-1
степенью свободы с помощью соотношений
:
распределения с N-1
степенью свободы с помощью соотношений
:
![]()
![]()
![]()
Доверительный интервал для а := (0,390091258, 0,635851914);
Доверительный
интервал для
![]() := (0,435626894,
0,696726491).
:= (0,435626894,
0,696726491).
7. По критерию проверим согласие эмпирических данных с нормальным распределением
![]()
Где
![]() -
функция распределения нормального
закона.
-
функция распределения нормального
закона.
Пусть
![]() равно числу элементов выборки ,попавших
в интервал [
равно числу элементов выборки ,попавших
в интервал [
![]() ), а
), а
![]() =
=
![]() - вероятность попадания в этот интервал,
если верна гипотеза
- вероятность попадания в этот интервал,
если верна гипотеза
![]() .
.
Границы интервалов:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
-1,167 |
-0,600 |
-0,300 |
0,000 |
0,350 |
0,500 |
0,700 |
1,000 |
1,300 |
1,700 |
2,262 |
Интервалы и данные для построения статистик:
|
|
a0-a1 |
a1-a2 |
a2-a3 |
a3-a4 |
a4-a5 |
a5-a6 |
a6-a7 |
a7-a8 |
a8-a9 |
a9-a10 |
|
n |
6 |
12 |
10 |
12 |
10 |
10 |
13 |
13 |
9 |
5 |
|
p |
0,0191 |
0,0468 |
0,1052 |
0,2098 |
0,1086 |
0,1445 |
0,1805 |
0,1112 |
0,0590 |
0,0137 |
|
Хи |
8,77 |
11,43 |
0,03 |
3,84 |
0,07 |
1,37 |
1,41 |
0,32 |
1,62 |
9,66 |
![]() =
38,5231;
=
38,5231;
![]() (
(![]() )
= 19,679016;
)
= 19,679016;
Т.к.
![]() >
>
![]() (
(![]() ),
то гипотеза
),
то гипотеза
![]() не верна.
не верна.
