Алгоритм построения сокращенной днф с помощью кнф (метод Нельсона)

Пусть f(x₁, … , x_n) есть некоторая функция алгебры логики. Построим для f некоторую КНФ. Осуществим далее следующие преобразования.

1. В КНФ раскроем скобки и удалим дублирующие члены, затем удалим дизъюнктивные слагаемые, содержащие одновременно переменную и ее отрицание. В результате получим дизъюнкцию конъюнкций, каждая из которых содержит только по одному элементу из каждой скобки КНФ.

2. В полученном выражении удалим нулевые дизъюнктивные слагаемые.

3. В полученном выражении проведем все поглощения, а затем удалим дублирующие члены.

В результате проведенных операций получим сокращенную ДНФ функции f. Покажем это.

Для каждой элементарной дизъюнкции D в КНФ и каждой элементарной конъюнкции K в сокращенной ДНФ (сокр. ДНФ) существует некоторый множитель вида x из K, содержащийся в D, т.е.

 D ДНФ  K  сокр. ДНФ  x^a  K (x^a D).

Допустим противное: в КНФ существует элементарная конъюнкция D, в сокращенной ДНФ существует элементарная конъюнкция K, для которой всякий множитель вида x^a из K не входит в D. Не уменьшая общности возьмем для простоты

Положим x₁ = a₁, …, x_k=a_k, x_k+1 = c_k+1  a_k+1, …, x_r = c_r  a_r. Тогда K(a₁, …, a_k) = 1, и потому f (a₁, …, a_k, c_k+1, …, c_r ) = 1. С другой стороны, D(c_k+1,…, c_r) = 0, и потому f (a₁, …, a_k, c_k+1, …, c_r ) = 0. Противоречие.

Пусть по-прежнему для простоты произвольный простой импликант K из сокращенной ДНФ равен . Тогда элементы попадут в не менее чем k скобок из КНФ. Если допустим, что этого нет, то при перемножении скобок из КНФ не получим дизъюнктивного слагаемого, которое содержало бы множители , а потому, строя из результата перемножения сокращенную ДНФ вычеркиванием лишних сомножителей, не получим простого импликанта K.

Так как содержатся в k разных скобках КНФ, а всякая другая скобка, отличная от указанных k скобок, содержит хотя бы один элемент вида x из K, то при раскрытии скобок имеем простой импликант K. После проведения всех операций поглощения и удаления дублирующих множителей, останутся только простые импликанты из сокращенной ДНФ, ибо если предположить наличие в результате хотя бы одного дизъюнктивного слагаемого, отличного от всех простых импликантов сокращенной ДНФ, то можно подобрать такие значения переменных функции f, на которых все простые импликанты примут значение 0, а это дополнительное слагаемое – значение 1, чего быть не может.

Пример 3. Построим сокращенную ДНФ этим способом для функции

f = (1111010010101111) из примера 1 :

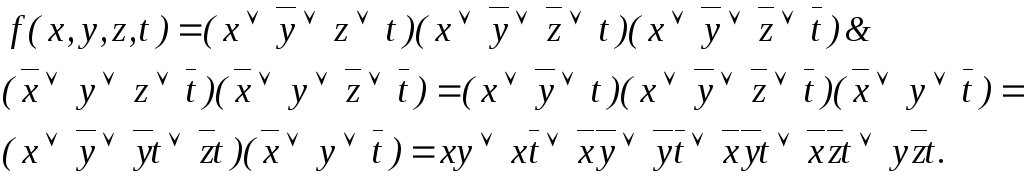
Сокращенная ДНФ для функции

что, естественно, совпадает с результатом примера 1.

Пример 4. Построить сокращенную ДНФ по заданной КНФ

После раскрытия скобок имеем:

После второго этапа получаем сокращенную ДНФ:

Тупиковой ДНФ ( ТДНФ) функции f называется такая ДНФ ее простых импликант, из которых нельзя выбросить ни одного импликанта, не изменив функции f.

Теорема. Всякая минимальная ДНФ некоторой функции является ее тупиковой ДНФ.

Доказательство. В МДНФ входят только простые импликанты, иначе некоторые множители в непростом имликанте можно удалить в противоречие с минимальностью исходной ДНФ. В МДНФ нет лишних импликант, иначе исходная ДНФ не является минимальной.

Вывод. Для получения МДНФ функции f необходимо построить все ТДНФ функции f и выбрать из них те, которые содержат минимальное число букв.