Элементы теории корреляции

Коэффициент корреляции является мерой линейной связи между зависимыми величинами. Он показывает, насколько хорошо, в среднем, может быть представлена (вычислена) одна из величин в виде линейной функции от другой.

Коэффициент корреляции вычисляется по формуле:

(3)

где 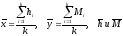— средние арифметические значения случайных величин h и M .

Коэффициент корреляции по абсолютной величине не превосходит 1. Чем ближе к 1, тем теснее линейная связь между h и M, и тем более справедлива аппроксимация таблично заданной функции линейной зависимостью.

Особо подчеркнем, что если коэффициент корреляции существенно меньше 1, это не означает отсутствие зависимости между параметрами h и M. Это означает только, что не применима линейная аппроксимация, но можно искать аппроксимирующую зависимость среди степенных, экспоненциальных, квадратичных и других классов функций.

Расчет коэффициента корреляции r в Mathcad, выдал результат: r=0.964846<1.Исходя из этого можно сделать вывод, что применима линейная аппроксимация между случайными величинами h и M. Следовательно, выбор линейной функции для аппроксимации был сделан верно.

Решение задачи в Mathcad Аппроксимация линейной функцей

Уравнение аппроксимируемой линии первой степени будет иметь вид:

(4)

Согласно методу наименьших квадратов наилучшими коэффициентами 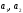, считаются те, для которых сумма квадратов отклонения теоретической функции от заданных эмпирических значений будет минимальной. Следовательно, задача состоит в определении коэффициентов _, таким образом, чтобы сумма квадратов отклонений была наименьшей.

Находим коэффициенты (пересечение графика с осью ОУ) и 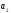(значение наклона), (т.к. любую прямую можно задать ее наклоном и У-пересечением) решая систему линейных уравнений, к которой нас приводит метод наименьших квадратов:

, (5)

где — коэффициенты аппроксимации.

Матрицу A составляем из коэффициентов левой части уравнения системы, а вектор 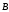из правой. Для нахождения коэффициентов используем метод:

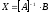
_где 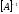матрица обратная матрице 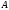, - вектор свободных членов. Тогда полученные составляющие вектора будут искомыми коэффициентами

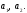
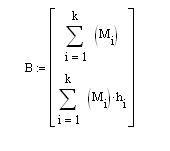
Рассчитаем обратную матрицу с помощью функции INVERSE в MathCAD

Получим:

Рассчитаем неизвестные коэффициенты:

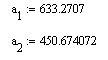
Подставим эти коэффициенты в линейную функцию:

Строим график который показывает, как полученная теоретическая функция описывает взаимосвязь между эмпирическими данными:

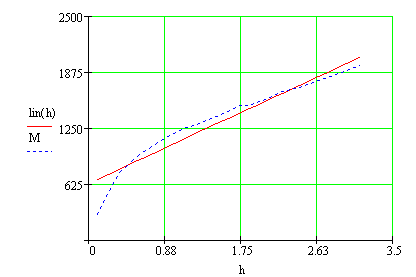
Рис. 5 График эмпирических данных и теоретической линейной функции.

Из графика видно, что уравнение линейной функции не достаточно хорошо отображает зависимость экспериментальных данных n и Q.

Аппроксимация квадратичной функции

Для случая квадратичной зависимости , неизвестные коэффициенты 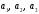мы находим, решая систему линейных алгебраических уравнений вида:

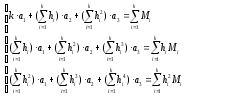
(6)

где k = 25, 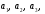- коэффициенты аппроксимации, h_i - i-ые значения толщины среза, M_i - i-ые значения момента нагрузки исполнительного органа угольного комбайна.

Матрицу A составляем из коэффициентов левой части уравнения системы, а вектор из правой. Для нахождения коэффициентов используем метод:

_где 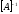матрица обратная матрице , 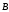- вектор свободных членов. Тогда полученные составляющие вектора 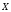будут искомыми коэффициентами

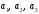
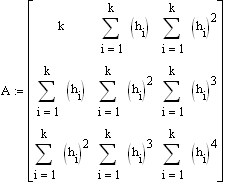
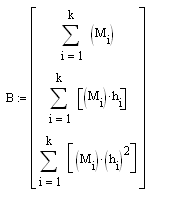
Рассчитаем обратную матрицу с помощью функции INVERSE в MathCAD

Получим:

Рассчитаем неизвестные коэффициенты:

Подставим эти коэффициенты в квадратичную функцию:

Строим график, который показывает, как полученная теоретическая функция описывает взаимосвязь между эмпирическими данными:

Рис. 6 График эмпирических данных и теоретической полиноминальной функции второй степени.

Из графика видно, что уравнение квадратичной функции лучше, чем уравнение линейной функции отображает зависимость экспериментальных данных M и h.