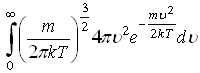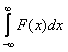4.2. Задачи
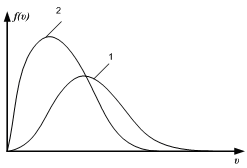
1НТ1(О). На рисунке
представлены распреде-ления Ферми-Дирака
по состояниям для двух систем частиц;
![]() ,
,
![]() .
Отношение масс частиц
.
Отношение масс частиц
![]() =
...
=
...
Ответ:
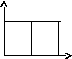
2.НТ1(О). На рисунке
представлены распреде-ления Ферми-Дирака
по состояниям для двух систем частиц;
![]() ,
,
![]() .
Отношение концентраций
.
Отношение концентраций
![]() ...
...
Ответ:
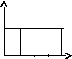
3.НТ1(О). На рисунке
представлены распреде-ления Ферми-Дирака
по энергиям для двух систем частиц;
![]() ,
,
![]() .
Отношение концентраций
.
Отношение концентраций
![]() ...
...
Ответ: 8
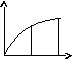
4.НТ1(О). На рисунке
представлены распреде-ления Ферми-Дирака
по энергиям для двух систем частиц ;
![]() ,
,
![]() .
Отношение концентраций
.
Отношение концентраций
![]() =
...
=
...
Ответ:2
 <n>
<n>
![]()
![]() ε
ε
2
<n>
![]()
![]() ε
ε
8

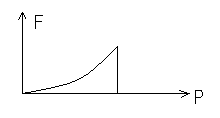
F
![]()
![]() ε
ε
 F
F
![]()
![]() ε
ε
5.НТ1(О). Энергия
Ферми металла
![]() эВ, квазиимпульс электронов при этой
энергии
эВ, квазиимпульс электронов при этой
энергии
![]() кг·м/c.
Масса свободного электрона
кг·м/c.
Масса свободного электрона
![]() кг,
эффективная масса электрона
кг,
эффективная масса электрона
![]() .
Отношение
.
Отношение
![]() равно ... Ответ округлить до целых.
равно ... Ответ округлить до целых.
Ответ:3
6.HT1(0).
Энергия Ферми металла
![]() эВ.
Эффективная масса электронов
эВ.
Эффективная масса электронов
![]() .
Максимальная скорость электронов при
Т=0 равна … км/с. Ответ округлить до
сотен.
.
Максимальная скорость электронов при
Т=0 равна … км/с. Ответ округлить до
сотен.
Ответ:1900
7.HT1(0).
Энергия Ферми металла
![]() эВ.
Эффективная масса электронов
эВ.
Эффективная масса электронов
![]()
![]() .
Средняя скорость электронов при Т=0
равна … км/с. Ответ округлить до сотен.
.
Средняя скорость электронов при Т=0
равна … км/с. Ответ округлить до сотен.
Ответ:1300
8.HT1(0).
Энергия Ферми для меди
![]() ,
для цинка
,
для цинка
![]() .
Эффективная масса электронов
.
Эффективная масса электронов
![]() .
Отношение концентраций свободных
электронов n2/n1
равно … . Ответ округлить до целых.
.
Отношение концентраций свободных
электронов n2/n1
равно … . Ответ округлить до целых.
Ответ:2
9.HT1(0).
Энергия Ферми для меди
![]() .
Средняя скорость электронов при Т=0
равна … . Ответ округлить до десятых.
.
Средняя скорость электронов при Т=0
равна … . Ответ округлить до десятых.
Ответ:4,2
10.HT1(0).
Средняя скорость электронов в калии
при Т=0 равна 1,2эВ. Эффективная масса
![]() .
Средняя скорость электронов при Т=0
равна … км/с. Ответ округлить до сотен.
.
Средняя скорость электронов при Т=0
равна … км/с. Ответ округлить до сотен.
Ответ:600
11.HT1(0).
Импульс, соответствующий энергии Ферми
![]() Масса электрона
Масса электрона
![]() .
Средняя энергия электронов равна … эВ.
Ответ округлить до целых.
.
Средняя энергия электронов равна … эВ.
Ответ округлить до целых.
Ответ:6
12.HT1(0). Если абсолютную температуру абсолютно черного тела увеличить в n=2 раза, его энергетическая светимость увеличивается в k раз.
Ответ:8
13. HT1
(0). Максимум спектральной энергетической
светимости излучения Солнца находится
при
![]() мкм. Постоянная в законе смещения Вина
b
=
мкм. Постоянная в законе смещения Вина
b
=
![]() Температура
на поверхности Солнца приблизительности
равна … К.
Температура
на поверхности Солнца приблизительности
равна … К.
Ответ:5800
14.HT1(
З). Температура абсолютного черного
тела равна Т=![]() К. Постоянная в законе смещения Вина в
=
К. Постоянная в законе смещения Вина в
=
![]()
Максимум спектральной плотности излучения находится при частоте
*А)
![]() В)
В)![]()
С)
![]() D)
D)
![]()
15.HT1(0).
Среднее время пролета валентного
электрона в поле действия ядра в кристалле
![]() Ширина валентной зоны
Ширина валентной зоны
![]() .
Постоянная Планка
.
Постоянная Планка
![]() .
Ответ округлить до десятых.
.
Ответ округлить до десятых.
Ответ:1,6
16.HT1(3).
В кристаллическом натрии электрон в
состоянии 1S
находится в поле действия ядра в среднем
![]() Ширина соответствующей уровню 1S
энергетической зоны равна … .
Ширина соответствующей уровню 1S
энергетической зоны равна … .
![]() .
.
А)
![]() *В)
*В)
![]() С)
С)
![]() D)
D)
![]()
17.HT1(3).
Ширина разрешенной энергетической зоны
![]() в одновалентном кристалле имеется N=
в одновалентном кристалле имеется N=![]() атомов. Расстояние между соседними
подуровнями в зоне равно
атомов. Расстояние между соседними
подуровнями в зоне равно
А) 1 эВ; * В)
![]() С)
С)
![]() D)
D)
![]()
18. НТ1(0). Ширина
запрещенной зоны в кремнии ![]() =1,1
эВ. Если температуру увеличить от
=1,1
эВ. Если температуру увеличить от
![]() =300К
до
=300К
до ![]() =400К,
концентрация электронов в зоне
проводимости увеличится в … раз.
Постоянная Больцмана к=0,86
=400К,
концентрация электронов в зоне
проводимости увеличится в … раз.
Постоянная Больцмана к=0,86![]() эВ/K.
Ответ округлить до сотен.
эВ/K.
Ответ округлить до сотен.
Ответ: 300
19. НТ1(0). Ширина
запрещенной зоны в кремнии ![]() =1,1
эВ. Если температуру увеличить от
=1,1
эВ. Если температуру увеличить от
![]() =300К
до
=300К
до ![]() =400К,
концентрация дырок в валентной зоне
увеличится в … раз. Постоянная Больцмана
к=0,86
=400К,
концентрация дырок в валентной зоне
увеличится в … раз. Постоянная Больцмана
к=0,86![]() эВ/K.
Ответ округлить до сотен.
эВ/K.
Ответ округлить до сотен.
Ответ: 300
20.НТ1(0). Температура полупроводника постоянна и меньше температуры истощения примеси. Если концентрацию донорной примеси увеличить в 16 раз, концентрация электронов в зоне проводимости увеличится в … раз.
Ответ: 4
21.НТ1(0). Температура примесного полупроводника постоянна и выше температуры истощения примеси. Если концентрацию донорной примеси увеличить в 8 раз, концентрация электронов в зоне проводимости увеличится в … раз.
Ответ: 8
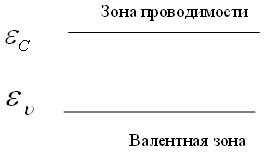
22.НТ2(0). Донорный
уровень фосфора ниже дна зоны проводимости
на ![]() =0,013
эВ в германии. Концентрация электронов
в зоне проводимости в кремнии n1
в германии-n2.
При Т=10К n2/n1=
=0,013
эВ в германии. Концентрация электронов
в зоне проводимости в кремнии n1
в германии-n2.
При Т=10К n2/n1=![]() ,
где x
равно … . Постоянная Больцмана к=0,86
,
где x
равно … . Постоянная Больцмана к=0,86![]() эВ/K.
Ответ округлить до целых.
эВ/K.
Ответ округлить до целых.
Ответ: 19
23.НТ2(0). Ширина
запрещенной зоны для германия ![]() ,
для кремния
,
для кремния ![]() =1,1
эВ. Концентрация электронов в зоне
проводимости для германия n1,
для кремния n2.
При Т=300К отношение n1/n2
равно … . Постоянная Больцмана к=0,86
=1,1
эВ. Концентрация электронов в зоне
проводимости для германия n1,
для кремния n2.
При Т=300К отношение n1/n2
равно … . Постоянная Больцмана к=0,86![]() эВ/К. Ответ округлить до десятков.
эВ/К. Ответ округлить до десятков.
Ответ: 1070
24. НТ1. При Т=0
химический потенциал собственного
полупроводника ![]() запрещенной
зоны рана … эВ.
запрещенной
зоны рана … эВ.
Ответ: 1
25. НТ1. При Т=0
химический потенциал полупроводника
n-типа
![]() =-0,005
эВ. Донорный уровень расположен ниже
дна зоны проводимости на … эВ.
=-0,005
эВ. Донорный уровень расположен ниже
дна зоны проводимости на … эВ.
Ответ: 0,01
1)Для
молекул
идеального газа значения интегралов
 и
и
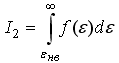 ,
где
,
где
![]() -
наиболее вероятная энергия:
-
наиболее вероятная энергия:
![]() I1<I2
I1<I2
![]() I1>I2НЕПРАВ
I1>I2НЕПРАВ
![]() нельзя
сравнить, не зная температуры
нельзя
сравнить, не зная температуры
![]() I1=
I2
I1=
I2
2)Функция распределения Бозе-Эйнштейна по энергиям имеет вид ...
![]()
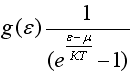
![]()
![]()
![]()
![]()
![]()
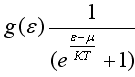
3)Для N квантовых частиц объем минимальной фазовой ячейки, приходящейся на одно квантовое микросостояние системы, ΔГmin равен:
![]() h3
h3
![]() →
0
→
0
![]() h3N
h3N
![]() h
НЕПРАВ
h
НЕПРАВ
4)Найдите соответствие между названиями величин из левого столбика и их аналитическими выражениями из правого. Ответ дайте в виде: k-l, m-n,…
|
|
|
5)Интеграл Найдите все возможные соответствия между левым и правым столбиками. Ответ дайте в виде: k-l, m-n, …
|
|
|
6)Формуле
планка
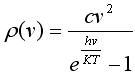 имеет
смысл ...
имеет
смысл ...
![]() Количества
фотонов, находящихся в единичном малом
интервале частот
Количества
фотонов, находящихся в единичном малом
интервале частот
![]() Количества
фотонов, проходящих в единицу времени
через единичную площадьНЕПРАВ
Количества
фотонов, проходящих в единицу времени
через единичную площадьНЕПРАВ
![]() Энергии
фотонов, находящихся в единичном малом
интервале частот НЕПРАВ
Энергии
фотонов, находящихся в единичном малом
интервале частот НЕПРАВ
7)Изменение
энтропии при переходе из состояния (1)
в состояние (2):

![]()
![]() нельзя
определить, так как неизвестно соотношение
температур
нельзя
определить, так как неизвестно соотношение
температур
![]()
![]()
![]()
![]()
![]()
![]()
8)Функция распределения Бозе-Эйнштейна по состояниям имеет вид ...
![]()
![]()
![]()

![]()
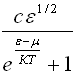 НЕПРАВ
НЕПРАВ
![]()
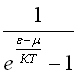
![]() Количестве
фотонов, излучаемых в единицу времени
с единичной площади
Количестве
фотонов, излучаемых в единицу времени
с единичной площади
9)Теплоемкость общей массы идеального одноатомного газа при V=const:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() НЕПРАВ
НЕПРАВ
10)![]() -
плотность вероятности или функция
распределения случайной величины х,
Нормированный множитель С равен:
-
плотность вероятности или функция
распределения случайной величины х,
Нормированный множитель С равен:
![]()

![]() 1
1
![]()
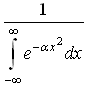
![]()

11)![]() -
плотности вероятности или функции
распределения молекул идеального газа
по проекциям скорости. Выражение
-
плотности вероятности или функции
распределения молекул идеального газа
по проекциям скорости. Выражение
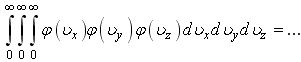
12)![]() -
плотность вероятности или функция
распределения молекул идеального газа
по модулю скорости, для которой справедливо
любое соотношение, кроме:
-
плотность вероятности или функция
распределения молекул идеального газа
по модулю скорости, для которой справедливо
любое соотношение, кроме:
![]()

![]()

![]()
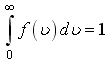
![]()
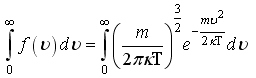
13) Функция распределения Бозе-Эйнштейна по состояниям может быть получена путём усреднения по формуле ...
![]()
![]() ,
где
,
где
![]() -
вероятность того, что на K-ом уровне
находится
-
вероятность того, что на K-ом уровне
находится
![]() частицНЕПРАВ
частицНЕПРАВ
![]()
![]() ,
где
,
где
![]() -
вероятность нахождения
-
вероятность нахождения
![]() частиц
в K-том состоянии
частиц
в K-том состоянии
![]()
![]() ,
где
,
где
![]() -
то же, что и в пункте С
-
то же, что и в пункте С
![]()
![]() ,
где
,
где
![]() -
то же, что и в пункте А
-
то же, что и в пункте А
14)Если
х - случайная физическая величина,
принимающая ряд дискретных значений
х1,х2,
… хn,
а Рi
– вероятность появления хi,
то
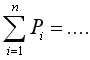
15)Для
электронного газа в металле
 имеет
смысл
имеет
смысл
![]() вероятности
нахождения электрона в интервале
вероятности
нахождения электрона в интервале
![]() НЕПРАВ
НЕПРАВ
![]() энергии
всех электронов в зоне проводимости
энергии
всех электронов в зоне проводимости
![]() количества
электронов в зоне проводимости
количества
электронов в зоне проводимости
![]() количества
состояний в зоне проводимости
количества
состояний в зоне проводимости
16)Отношение
интегралов для молекулы водорода Н2
(молярная масса водорода 2·10-3кг/моль)
при Т=300 К с учетом NA≈6·10231/моль
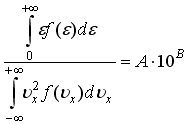 ,
где
A и B – целые числа, значения которых
перечислите через точку с запятой … ,
… без учета размерностей.
,
где
A и B – целые числа, значения которых
перечислите через точку с запятой … ,
… без учета размерностей.
17)Функция распределения частиц по энергиям в квантовой статистике – это …
![]() среднее
число частиц с энергией
среднее
число частиц с энергией
![]()
![]() вероятность
нахождения частицы с энергией
вероятность
нахождения частицы с энергией
![]() НЕПРАВ
НЕПРАВ
![]() среднее
число частиц в одном квантовом состоянии
с энергией
среднее
число частиц в одном квантовом состоянии
с энергией
![]()
![]() среднее
число частиц в малом единичном интервале
энергии
среднее
число частиц в малом единичном интервале
энергии
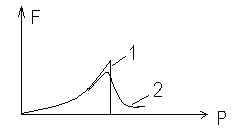
18)На
рисунке приведены графики изохоры,
изобары, изотермы, адиабаты. Правильные
названия графиков:
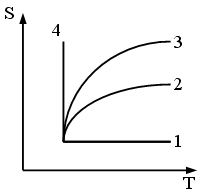
![]() 1-изотерма,
2-изохора, 3-изобара, 4-адиабата
1-изотерма,
2-изохора, 3-изобара, 4-адиабата
![]() 1-адиабата,
2-изохора, 3-изобара, 4-изотерма
1-адиабата,
2-изохора, 3-изобара, 4-изотерма
![]() 1-изотерма,
2-изохора, 3-изобара, 4-адиабата
1-изотерма,
2-изохора, 3-изобара, 4-адиабата
![]() 1-изохора,
2-изобара, 3-адиабата, 4-изотерма
1-изохора,
2-изобара, 3-адиабата, 4-изотерма
19)Для
функций распределения
 и
и
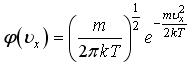 справедливо
соотношение:
справедливо
соотношение:
![]()

![]()
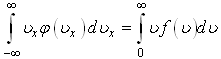
![]()

![]()
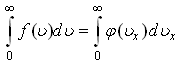 НЕПРАВ
НЕПРАВ
20)Распределение фононов по состояниям имеет вид:
![]()
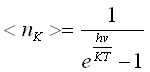
![]()
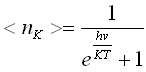 НЕПРАВ
НЕПРАВ
![]()

![]()

21)При одинаковых температурах средняя квадратичная скорость молекул кислорода ………средней квадратичной скорости молекул водорода. Вставьте слово.
МЕНЬНЕ-НЕПРАВ
22)Запишите
формулу для количества квантовых
состояний, соответствующих интервалу
модуля скорости
![]() и
объему V, используя шаблон
и
объему V, используя шаблон
![]()
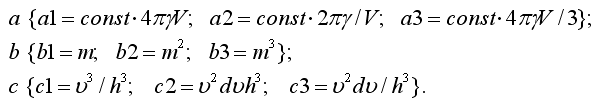
23)Запишите
формулу для количества квантовых
состояний, соответствующих интервалу
![]() и
объему V, используя шаблон
и
объему V, используя шаблон
![]()
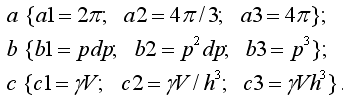
24)Наиболее вероятное значение энергии для молекул идеального газа:
![]()
![]() НЕПРАВ
НЕПРАВ
![]() не
зависит от
не
зависит от
![]()
![]()
![]()
![]()
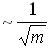
25)Энергия
Ферми металла
![]() эВ.
Эффективная масса электронов
эВ.
Эффективная масса электронов
![]() .
Максимальная скорость электронов при
Т=0 равна … км/с. Ответ округлить до
сотен.
.
Максимальная скорость электронов при
Т=0 равна … км/с. Ответ округлить до
сотен.
26)Каноническое
распределение Гиббса имеет вид
![]() ,
где постоянная С равна :
,
где постоянная С равна :
![]()
 НЕПРАВ
НЕПРАВ
![]()
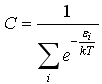
![]()
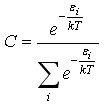
![]()
![]()
27)Ширина
разрешенной энергетической зоны
![]() в
одновалентном кристалле имеется N=1022
атомов. Расстояние между соседними
подуровнями в зоне равно
в
одновалентном кристалле имеется N=1022
атомов. Расстояние между соседними
подуровнями в зоне равно
![]()
![]() НЕПРАВ
НЕПРАВ
![]() 1
Эв НЕПРАВ
1
Эв НЕПРАВ
![]()
![]()
![]()
![]()
28)Если
число молекул идеального газа выросло
в четыре раза (N2=4N1),
а
![]() и
и
![]() ,
то относительное число молекул, имеющих
скорости от
,
то относительное число молекул, имеющих
скорости от
![]() до
до
![]() :
:
![]() уменьшилось
в 4 раза неправ
уменьшилось
в 4 раза неправ
![]() увеличилось
в 2 раза
увеличилось
в 2 раза
![]() осталось
прежним
осталось
прежним
![]() увеличилось
в 4 разаНЕПРАВ
увеличилось
в 4 разаНЕПРАВ
29)Правильным
соотношением для функции распределения
молекул идеального газа по проекции
импульса
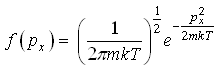 является:
является:
![]()

![]()
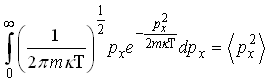
![]()
 неправ
неправ
![]()
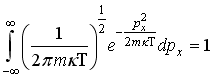
30)Для
функций распределения Максвелла по
проекциям импульсов
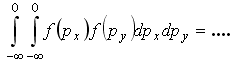
0-НЕПРАВ
31)Запишите
формулу для фазового объема, соответствующего
интервалу
![]() и
объему V, используя шаблон
и
объему V, используя шаблон
![]()

32)Запишите
формулу для распределения Бозе-Эйнштейна
по состояниям, используя шаблон
![]()

33)Если
![]() -
функции распределения по проекциям
скоростей для молекул идеального газа,
то:
-
функции распределения по проекциям
скоростей для молекул идеального газа,
то:
![]()
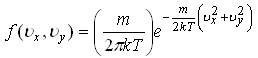
![]()
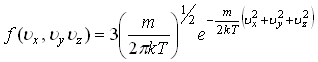 НЕПРАВ
НЕПРАВ
![]()
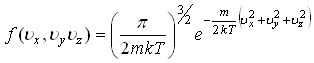
![]()
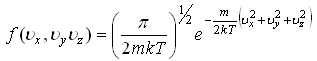 НЕПРАВ
НЕПРАВ
34)Отношение теплоёмкости вырожденного электронного газа и теплоёмкости не вырожденного классического газа равно:
![]()
![]() НЕПРАВ
НЕПРАВ
![]()

![]()
![]()
![]()
![]() НЕПРАВ
НЕПРАВ
35)F(x)
– плотность вероятности или функция
распределения случайной величины х.
Среднее значение
![]() равно:
равно:
![]()
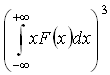
![]()

![]()

![]()

36)В модели Эйнштейна - Дебая постулируется, что N атомов кристалла должны иметь ...
![]() бесконечное
число колебательных мод с одинаковой
скоростью
бесконечное
число колебательных мод с одинаковой
скоростью
![]() бесконечное
число колебательных мод с фазовой
скоростью
бесконечное
число колебательных мод с фазовой
скоростью
![]()
![]() 3N
колебательных мод с одинаковой фазовой
скоростью
3N
колебательных мод с одинаковой фазовой
скоростью
![]() 3N
колебательных мод с фазовой скоростью
3N
колебательных мод с фазовой скоростью
![]() НЕПРАВ
НЕПРАВ
37)Если
F(x) – плотность вероятности или функция
распределения случайной величины х, то
выражение
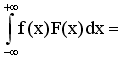
38)Зонный характер энергетического спектра электронов в кристаллах связан с . . .
![]() вырождением
состояний по магнитному квантовому
числу
вырождением
состояний по магнитному квантовому
числу
![]() вырождением
состояний по орбитальному квантовому
числуНЕПРАВ
вырождением
состояний по орбитальному квантовому
числуНЕПРАВ
![]() перекрытием
волновых функций электронов из соседних
атомов
перекрытием
волновых функций электронов из соседних
атомов
![]() рассеянием
электронов на колебаниях атомов
рассеянием
электронов на колебаниях атомов
39)Для данного газа в равновесном состоянии отношение средней энергии частиц к наиболее вероятной энергии при заданной температуре равно…
40)Среднее
время пролета валентного электрона в
поле действия ядра в кристалле
![]() Ширина
валентной зоны
Ширина
валентной зоны
![]() .
Постоянная Планка
.
Постоянная Планка
![]() .
Ответ округлить до десятых.
.
Ответ округлить до десятых.
41)Энергия
Ферми металла
![]() эВ,
квазиимпульс электронов при этой энергии
эВ,
квазиимпульс электронов при этой энергии
![]() кг•м/c.
Масса свободного электрона
кг•м/c.
Масса свободного электрона
![]() кг,
эффективная масса электрона
кг,
эффективная масса электрона
![]() .
Отношение
.
Отношение
![]() равно
... Ответ округлить до целых.
равно
... Ответ округлить до целых.
42)Основной постулат статической физики утверждает, что микросостояния, принадлежащие одной …. , равновероятны
43)Для невырожденного полупроводника функция распределения электронов по энергиям в зоне проводимости имеет вид…
![]()
![]()
![]()
![]()
![]()

![]()
![]()
----------------------------------------------------------------------------------------------------------------------------------------------------
44)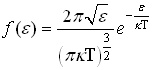 -
плотность вероятности или функция
распределения молекул идеального газа
по энергии. Среднее значение
-
плотность вероятности или функция
распределения молекул идеального газа
по энергии. Среднее значение
![]() молекулы
идеального газа равно:
молекулы
идеального газа равно:
![]()
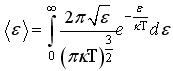
![]()
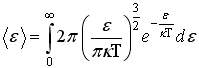
![]()
 НЕПРАВ
НЕПРАВ
![]()

45)При T=const максимальное значение функции распределения по проекции импульса f(px):
![]()
![]()
![]()
![]()
![]()
![]()
![]() не
зависит от
не
зависит от
![]()
![]()

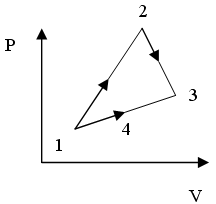
46)Изменение
энтропии
![]() и
и
![]() для
процессов, изображенных на P-T диаграмме:
для
процессов, изображенных на P-T диаграмме:
![]()
![]() НЕПРАВ
НЕПРАВ
![]()
![]()
![]()
![]()
![]()
![]()
47)Энергия Ферми
![]() ,
средняя энергия фермионов при Т=0
,
средняя энергия фермионов при Т=0
![]() .
Отношение
.
Отношение
![]() ...
Округлить до десятых.
...
Округлить до десятых.
48)Плотность
вероятности или функция распределения
молекул идеального газа по проекции
скорости имеет вид
![]() ,
где нормированный множитель C равен:
,
где нормированный множитель C равен:
![]()
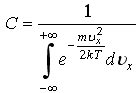
![]()
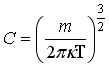
![]()
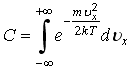 неправ
неправ
![]()

49)При Т=const максимальное
значение плотности вероятности
![]() с
увеличением массы молекул ……. Вставьте
слово.
с
увеличением массы молекул ……. Вставьте
слово.
Уменьшаеться-неправ
50)Для каждого типа частиц выберите их свойства:
|
|
|
Если
![]() –
функция распределения молекул идеального
газа по проекции скорости, то для
интегралов:
–
функция распределения молекул идеального
газа по проекции скорости, то для
интегралов:
 ,
,
 ,
,
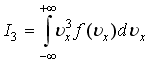 справедливо
следующее соотношение:
справедливо
следующее соотношение:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() неправ
неправ
![]()
![]()
![]()
![]()
+ 1)Для циклического
процесса, изображенного на рис:
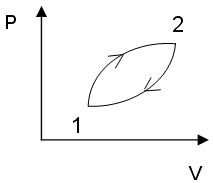
![]()
![]()
+ 2) Основной постулат квантовой статистики - это ...
![]() принцип
тождественности частиц
принцип
тождественности частиц
+ 3) Плотность квантовых состояний в энергетическом пространстве – это ...
![]() число
состояний в единичном малом интервале
энергии
число
состояний в единичном малом интервале
энергии
+ 4) F(x) – плотность
вероятности или функция распределения
случайной величины х. Среднее значение
![]() на
интервале от х1 до х2 равно:
на
интервале от х1 до х2 равно:
![]()

+ 5) Графики 1,2,3 соответствуют
трем функциям распределения Максвелла
по модулю импульса для одного и того же
газа в сосуде V при разных T. Наименьшей
энтропии соответствует график …..
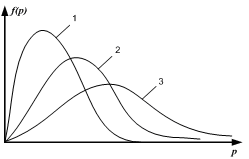 Ответ: 1
Ответ: 1
+ 6) На рисунке показано
распределение Максвелла по модулю
скорости для некоторого газа при разных
температурах. При этом площади под
кривыми (Si) и температуры (Тi)
удовлетворяют соотношению:
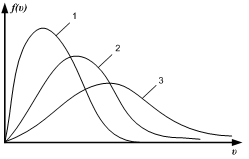
![]()
![]()
+ 7) Распределение электронов по состояниям в зоне проводимости невырожденного полупроводника приведено на рис. ...
![]()

+ 8) Концентрация электронов в зоне проводимости собственного полупроводника возрастает с повышением Т за счёт перехода электронов
![]() из
валентной зоны в зону проводимости
из
валентной зоны в зону проводимости
+ 9) На рисунке приведено
распределение Бозе-Эйнштейна для двух
температур. Соотношение температур T2
… T1.
 Для
кривых выполняется соотношение:
Для
кривых выполняется соотношение:
![]()
![]()
+ 10) Если функция
распределения по энергии для молекул
идеального газа пронормирована на число
частиц
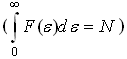 ,
то интеграл
,
то интеграл
 равен:
равен:
![]() суммарной
энергии всех частиц, у которых
суммарной
энергии всех частиц, у которых
![]()
+ 11) Функция распределения
Ферми-Дирака по энергиям имеет вид...
![]()
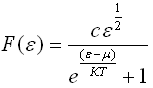
+ 12) Газ из состояния (1)
переходит в состояние (2) в одном случае
по прямой 1-2 , а в другом – по линии
1-3-4-2. При этом изменение энтропии:

![]()
![]()
+ 13) Вероятность Р наступления любого из двух независимых событий А или В равна:
![]() сумме
вероятностей Р(А)+Р(В)
сумме
вероятностей Р(А)+Р(В)
+14) На рисунке приведено
распределение Ферми-Дирака по энергиям.
Площадь заштрихованной области
соответствует ...
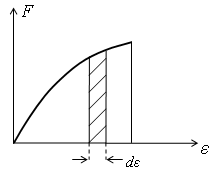
![]() числу
частиц, энергия которых находится в
интервале
числу
частиц, энергия которых находится в
интервале
![]()
+ 15) Распределение электронов по энергиям в зоне проводимости невырожденного полупроводника приведено на рис. ...
![]()

+ 16) Функция распределения молекул
идеального газа по проекции скорости
![]() ,
пронормированная на 1, имеет вид:
,
пронормированная на 1, имеет вид:
![]()
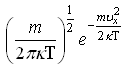
+ 17) Объем элементарной фазовой ячейки для одной квантовой частицы равен:
![]() h3
h3
+ 18) Функция распределения Ферми-Дирака по энергиям при Т=0 представлена на рисунке...
![]()

+ 19) Одному квантовому состоянию для N частиц (без учёта спина) соответствует фазовый объём …
![]() h3N
h3N
+ 20) Функции распределения молекул
идеального газа по проекции скорости
(плотность вероятности)
![]() для
разных газов, у которых m2>m1,
a T1=T2, показаны на рисунке:
для
разных газов, у которых m2>m1,
a T1=T2, показаны на рисунке:
![]()

+ 21) На рисунке приведено распределение
Ферми-Дирака.
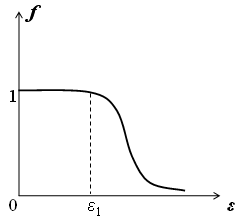 Состояния
с энергиями в интервале
Состояния
с энергиями в интервале
![]() заполнены
...
заполнены
...
![]() полностью,
в каждом находится один фермион
полностью,
в каждом находится один фермион
+ 22) Химический потенциал собственного полупроводника при Т=0 находится
![]() в
середине запрещенной зоны
в
середине запрещенной зоны
+ 23) Функция распределения
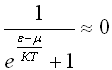 .
Это означает, что ...
.
Это означает, что ...
![]()
![]()
+ 24)
![]() -
плотность вероятности или функция
распределения молекул идеального газа
по энергии. Заштрихованная площадь
равна:
-
плотность вероятности или функция
распределения молекул идеального газа
по энергии. Заштрихованная площадь
равна:

![]() относительному
числу молекул
относительному
числу молекул
![]() ,
имеющих энергию от
,
имеющих энергию от
![]() до
до
![]()
+ 25) На рисунке изображена функция
распределения Ферми-Дирака по энергиям
при разных температурах.
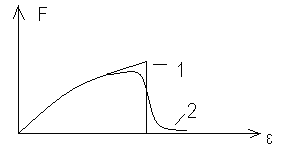 Кривая
1 соответствует Т1
Кривая 2
соответствует Т2
Кривая
1 соответствует Т1
Кривая 2
соответствует Т2
![]() Т1=0;
Т2>0
Т1=0;
Т2>0
+ 26) Если
![]() -
плотность вероятности или функция
распределения случайной величины х ( х
изменяется от - ∞ до + ∞), то справедливо
любое выражение, кроме:
-
плотность вероятности или функция
распределения случайной величины х ( х
изменяется от - ∞ до + ∞), то справедливо
любое выражение, кроме:
![]()

+ 27) Из приведенных величин: m –масса газа, S – энтропия, Т –температура, V –объем, Ω -статистический вес, n –концентрация частиц, p –давление - аддитивными являются:
![]() m,
S, V
m,
S, V
+ 28) Для распределения Ферми-Дирака по
энергии выражение
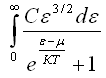 имеет
смысл …
имеет
смысл …
![]() общая
энергия всей системы фермионов
общая
энергия всей системы фермионов
+29) Основной постулат квантовой статистики (принцип тождественности) является следствием того, что ...
![]() описание
движения отдельной частицы носит
вероятностный характер
описание
движения отдельной частицы носит
вероятностный характер
+ 30) Одному квантовому состоянию (без учёта спина) соответствует фазовый объём …
![]()
![]()
+ 31) Система фононов описывается статистикой
![]() Бозе-Эйнштейна
Бозе-Эйнштейна
+ 32) На рисунке приведено распределение
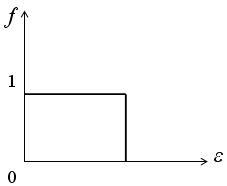
![]() Ферми-Дирака
по состояниям при
Ферми-Дирака
по состояниям при
![]()
+ 31) Между свободной и валентной зонами
находится запрещённая зона шириной
![]() Валентная
зона при
Валентная
зона при
![]() заполнена
на половину. Кристалл является . . .
заполнена
на половину. Кристалл является . . .
![]() проводником
проводником
+ 32) Принцип Паули утверждает, что ...
![]() в
одном квантовом состоянии может
находиться не более одного фермиона
в
одном квантовом состоянии может
находиться не более одного фермиона
+ 33) При увеличении температуры основная причина роста электропроводности собственного полупроводника …
![]() увеличение
концентрации носителей тока
увеличение
концентрации носителей тока
+ 34) Вероятность Р одновременного наблюдения 2-х независимых событий А и В равна:
![]() произведению
вероятностей Р(А)•Р(В)
произведению
вероятностей Р(А)•Р(В)
+ 35) Одному квантовому состоянию для одной частицы в трехмерном пространстве соответствует фазовый объем
![]()
![]()
+ 36) Функция распределения Ферми-Дирака
по модулю импульса при Т=0 представлена
на рисунке …
![]()

+ 37) Среднее значение
![]() можно
найти, пользуясь любым выражением,
кроме…
можно
найти, пользуясь любым выражением,
кроме…
![]()

+ 38) Каждому типу полупроводника проводника выберите энергетическую диаграмму
|
|
· 2 · 1 · 3 |
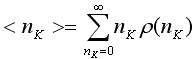 ,
где K – это …
,
где K – это …
![]() набор
квантовых чисел, задающих данное
квантовое состояние свободного бозона
набор
квантовых чисел, задающих данное
квантовое состояние свободного бозона
+ 40) Изменение энтропии
![]() при
плавлении льда (m-масса, λ -удельная
теплота плавления) равно:
при
плавлении льда (m-масса, λ -удельная
теплота плавления) равно:
![]()
![]()
+ 41) Статический вес системы:
![]() зависит
от числа частиц системы
зависит
от числа частиц системы
+42) Зависимость теплоёмкости твёрдого тела от температуры приведена на графикe …
![]()
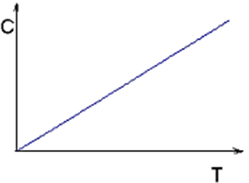
+ 43) Функции распределения по проекции импульса рх (плотность вероятности) для разных газов, у которых m2>m1, а T1=T2, показаны на рисунке:
![]()
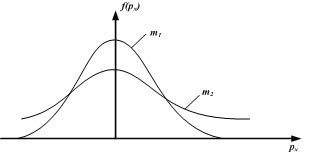
+ 44) Распределение Больцмана
![]() применимо
для ...
применимо
для ...
![]() систем
частиц малой плотности, у которых не
проявляются квантовые свойства
систем
частиц малой плотности, у которых не
проявляются квантовые свойства
+ 45) Распределение Максвелла по модулю скорости для некоторого идеального газа при Т1>Т2 показано на рисунке:
![]()
+ 46) Формула
![]() представляет
собой зависимость химического потенциала
от температуры для ...
представляет
собой зависимость химического потенциала
от температуры для ...
![]() собственного
полупроводника
собственного
полупроводника
+ 47) Функция распределения Ферми-Дирака по состояниям может быть получена, исходя из формулы:
![]()
![]() ,
где
,
где
![]() вероятность
нахождения
вероятность
нахождения
![]() фермионов
в k -том квантовом состоянии
фермионов
в k -том квантовом состоянии
+ 48) При конденсации пара энтропия системы:
![]() уменьшается
уменьшается
+ 49) На рисунке приведено распределение
Ферми-Дирака. Интервал энергий
![]() примерно
равен…
примерно
равен…

![]() 2KT
2KT
+ 50) Вероятность достоверного события равна ….Ответ: 1
+ 51) Реальные процессы в изолированных системах протекают:
![]() в
направлении увеличения хаотичности
движения частиц в системе
в
направлении увеличения хаотичности
движения частиц в системе
+ 52) Для электронов в зоне проводимости невырожденного полупроводника следует применить распределение … Укажите все возможные варианты.
![]() Максвелла
Максвелла
![]() Ферми-Дирака
Ферми-Дирака
+53) Если F(x) – функция распределения
случайной величины х, а f(x2) –
некоторая функция этой величины, то
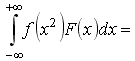
![]()
![]()
+ 54) Распределение Бозе-Эйнштейна по энергиям – это …
![]() среднее
число бозонов в единичном малом интервале
энергии
среднее
число бозонов в единичном малом интервале
энергии
+ 55) Если свойства системы частиц сильно зависят от квантовых свойств частиц, система является ...
![]() определить
нельзя
определить
нельзя
![]() классической
классической
![]() вырожденной
вырожденной
![]() невырожденной
невырожденной
+ 56) На рисунке приведено распределение
Ферми-Дирака.
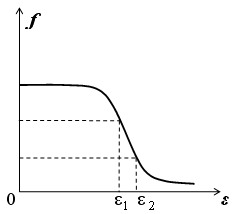 Каждое
состояние с энергией в интервале
Каждое
состояние с энергией в интервале
![]() заполнено
заполнено
![]() Частично
Частично
+ 57) Неправильным утверждением является. Вероятность случайного события Р:
![]() Р
изменяется от 0 до ∞
Р
изменяется от 0 до ∞
+ 58) Второе начало термодинамики утверждает, что в замкнутой системе:
![]() ΔS≥0
ΔS≥0
+ 59) Теплоёмкость электронного газа в металлах …
![]()
![]() т.к.
средняя энергия теплового движения
электронов в металле
т.к.
средняя энергия теплового движения
электронов в металле
![]()
+ 60) Энергетический спектр электронов в кристаллах . . .
Или этот * состоит из разрешённых и запрещённых зон одинаковой ширины
* сплошной
* состоит из дискретных уровней, разделённых большими промежутками
Или этот * состоит из разрешённых и запрещённых зон одинаковой ширины
+ 61) Молекулы идеального газа :
![]() могут
иметь как целый, так и полу целый спин
могут
иметь как целый, так и полу целый спин
+ 62) Условием нормировки функции распределения Максвелла по модулю скорости для молекул идеального газа является выражение:
![]()

+ 63) Изменение энтропии при изотермическом
квазиравновесном процессе 1-2:

![]() ΔS12
= 0
ΔS12
= 0
+ 64) Функция распределения Ферми-Дирака
по состояниям находится по формуле
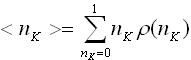 ,
где k – это ...
,
где k – это ...
![]() Набор
квантовых чисел, задающих квантовое
состояние частицы в атоме
Набор
квантовых чисел, задающих квантовое
состояние частицы в атоме
+ 65) Функция распределения частиц по энергиям в квантовой статистике определяется по формуле …
![]()
![]()
+66) В равновесной системе
![]()
![]() 0
0
+ 67) Для кристалла, состоящего из N атомов
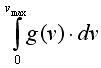 равен
равен
![]() 3N
3N
+ 68) Функция распределения молекул
идеального газа по модулю скорости
![]() (плотность
вероятности) имеет размерность:
(плотность
вероятности) имеет размерность:
![]()
![]()
69)
+ 70) При равновесном тепловом излучении тело излучает и поглощает одно и то же количество энергии ...
![]() за
одно и то же время с одной и той же площади
в одном и том же интервале частот dν
за
одно и то же время с одной и той же площади
в одном и том же интервале частот dν
+71) Носителями тока в собственном полупроводнике являются …
![]() электроны
в зоне проводимости и дырки в валентной
зоне
электроны
в зоне проводимости и дырки в валентной
зоне
+ 72) Термодинамическая система находится в равновесном состоянии, если:
![]()
![]()
+ 73) Концентрация электронов собственного полупроводника зависит от температуры следующим образом …
![]()
![]()
+ 74) Энергия Ферми – это …
![]() максимальная
энергия фермионов при Т=0
максимальная
энергия фермионов при Т=0
+75) F(x) – плотность вероятности или
функция распределения случайной величины
х. Среднее значение
![]() равно:
равно:
![]()

76)
+ 77) Формула для концентрации электронов в зоне проводимости полупроводника n-типа имеет вид ...
![]()
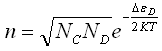
+ 78) При высоких температурах
![]() теплопроводность
твердого тела зависит от температуры
по закону ...
теплопроводность
твердого тела зависит от температуры
по закону ...
![]()
![]() ,
т.к. энергия колебаний ∼T,
а количество возбуждённых мод не меняется
нет
,
т.к. энергия колебаний ∼T,
а количество возбуждённых мод не меняется
нет
+ 79) Наиболее вероятное значение проекции
скорости
![]() для
молекул идеального газа равно:
для
молекул идеального газа равно:
![]() 0
0
80)
+ 81) Распределение Больцмана по состояниям имеет вид ...
![]()
![]()
+ 82)
![]() -
это
-
это
![]() средняя
квадратичная скорость, где m – масса
одной молекулы
средняя
квадратичная скорость, где m – масса
одной молекулы
+ 83) Для получения полупроводника n-типа подбирают пятивалентную примесь, донорный уровень которой находится ...
![]() в
запрещённой зоне вблизи дна зоны
проводимости
в
запрещённой зоне вблизи дна зоны
проводимости
+ 84) Для получения полупроводника p-типа подбирают трехвалентную примесь, акцепторный уровень которой находится …
![]() в
запрещённой зоне вблизи потока валентной
зоны
в
запрещённой зоне вблизи потока валентной
зоны
+ 85) Энергия квантового гармонического осциллятора равна
![]()
![]()
+ 86) Точка в фазовом пространстве для системы из N частиц характеризует:
![]() положение
в пространстве отдельной частицы
положение
в пространстве отдельной частицы
![]() микросостояние
системы
микросостояние
системы
![]() макросостояние
системы
макросостояние
системы
![]() микросостояние
отдельной частицы
микросостояние
отдельной частицы
87)
88)
89)
+ 90) Средние скорости молекул идеальных
газов, у которых
![]() ,
а массы молекул
,
а массы молекул
![]()
![]()
![]()
+ 91) Длина волны де Бойля
![]() ,
среднее расстояние между частицами l.
Для невырожденной системы выполняется
условие ...
,
среднее расстояние между частицами l.
Для невырожденной системы выполняется
условие ...
![]()
![]()
+ 92) В замкнутой системе энтропия может
меняться со временем, как показано на
участках:

![]() 1-2-3
1-2-3
+ 93) Отношение электронной и решеточной
теплоёмкостей для твёрдого тела при
высоких температурах
![]() составляет
…
составляет
…
![]()
94)
+ 95) функция распределения Ферми-Дирака по модулю квазиимпульса равна …
![]()
![]()
96)
97)
98)
99)
+ 100)
![]() -
плотности вероятности или функции
распределения молекул по проекциям
скорости, для которых справедливо любое
соотношение, кроме…
-
плотности вероятности или функции
распределения молекул по проекциям
скорости, для которых справедливо любое
соотношение, кроме…
![]()
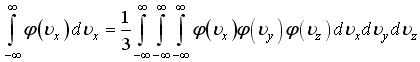
+ 101) Необходимым и достаточным условием равновесного состояния системы является:
![]() стационарность
макро- и микропараметров
стационарность
макро- и микропараметров
![]() замкнутость
системы и стационарность микропараметров
замкнутость
системы и стационарность микропараметров
![]() замкнутость
системы и стационарность макропараметров
замкнутость
системы и стационарность макропараметров
![]() стационарность
макропараметров
стационарность
макропараметров
+ 102) В одновалентных металлах валентная зона заполнена …
![]() на
две трети
на
две трети
![]() наполовину
наполовину
![]() на
одну треть
на
одну треть
![]() полностью
полностью
+ 103) Если
![]() -
плотность вероятности или функция
распределения молекул идеального газа
по энергии, то среднее значение
-
плотность вероятности или функция
распределения молекул идеального газа
по энергии, то среднее значение
![]() на
интервале энергий от
на
интервале энергий от
![]() до
до
![]() равно:
равно:
![]()

+ 104) Число возможных состояний системы
из N =100 квантовых частиц (электронов) в
конечном элементе объема
![]() равно:
равно:
![]()
![]()

![]()
1.В интервале
![]() число
квантовых состояний
число
квантовых состояний
![]() ,
число частиц
,
число частиц
![]() .
Для невырожденной системы выполняется
условие
.
Для невырожденной системы выполняется
условие
![]()
![]()
2. Плотность квантовых состояний в энергетическом пространстве – это ...
![]() число
состояний в единичном малом интервале
энергии
число
состояний в единичном малом интервале
энергии
3. Перейти от
классической функции распределения по
модулю скорости
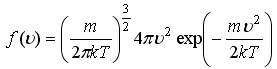 к
функции распределения по энергии f(e)
к
функции распределения по энергии f(e)
![]() можно,
заменив
можно,
заменив
![]() на
на
![]() в
выражении
в
выражении
![]()
![]() можно,
заменив
можно,
заменив
![]() на
на
![]() и
и
![]() на
на
![]() в
выражении
в
выражении
![]()
![]() можно,
заменив
можно,
заменив
![]() на
на
![]() и
и
![]() на
на
![]() в
выражении
в
выражении
![]()
![]() нельзя
ни одним из этих преобразований
нельзя
ни одним из этих преобразований
4. Функция распределения Бозе-Эйнштейна по состояниям имеет вид ...
![]()
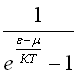
5. Запишите формулу для среднего количества
фермионов в одном квантовом состоянии
при заданной энергии ε, используя шаблон
![]()
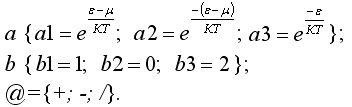
6.
![]() -
это
-
это
![]() средняя
квадратичная скорость, где m
– масса одной молекулы
средняя
квадратичная скорость, где m
– масса одной молекулы
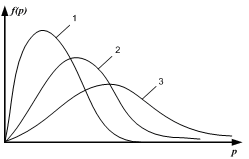
7. Графики 1,2,3 соответствуют трем функциям
распределения Максвелла по модулю
импульса для одного и того же газа в
сосуде V при разных T. Наименьшей энтропии
соответствует график …..
8.
![]() если:
если:
![]() V=const,
T=const
V=const,
T=const
![]() нет
правильного ответа
нет
правильного ответа
![]() P=const,
T=const
P=const,
T=const
![]() p=const,
S=cons
p=const,
S=cons
9. Каждому типу полупроводника проводника выберите энергетическую диаграмму
|
|
|
10. При Т=0 химический потенциал собственного полупроводника μ= –0,5 эВ. Ширина запрещенной зоны рана … эВ.
11. В собственном полупроводнике проводимость обусловлена переходом электронов …
![]() из
валентной зоны в зону проводимости
из
валентной зоны в зону проводимости
12.
 -
плотность вероятности или функция
распределения молекул идеального газа
по энергии. Среднее значение
-
плотность вероятности или функция
распределения молекул идеального газа
по энергии. Среднее значение
![]() молекулы
идеального газа равно:
молекулы
идеального газа равно:
![]()
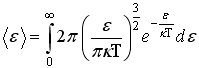
13. Для равновесия двух подсистем замкнутой системы достаточно, чтобы у них были равны только:
![]()
![]()
14. В равновесном состоянии с ростом числа частиц N, относительная флуктуация δ ∼ Nm, где m=…
15. Для функций
распределения Максвелла по проекциям
импульсов
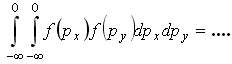 1/4
1/4
16. Формула для концентрации электронов в зоне проводимости полупроводника n-типа имеет вид ...
![]()

17. На рисунке
приведено распределение Ферми-Дирака.
Интервал энергий
![]() примерно
равен…
примерно
равен…
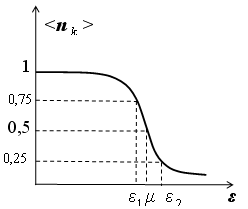
![]() 2KT
2KT
18. Химический потенциал собственного полупроводника при Т=0 находится
![]() в
середине запрещенной зоны
в
середине запрещенной зоны
19. При равновесном тепловом излучении тело излучает и поглощает одно и то же количество энергии ...
![]() за
одно и то же время с одной и той же площади
в одном и том же интервале частот dν
за
одно и то же время с одной и той же площади
в одном и том же интервале частот dν
20. Значения
интегралов
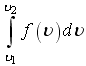 для
разных газов
для
разных газов
![]() при
одинаковых температурах:
при
одинаковых температурах:
![]() нельзя
сравнить, так как значения интеграла
зависят от выбранного интервала скоростей
нельзя
сравнить, так как значения интеграла
зависят от выбранного интервала скоростей
21. Функция
распределения
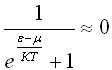 .
Это означает, что ...
.
Это означает, что ...
![]()
![]()
22. Функция распределения Ферми-Дирака по состояниям может быть получена, исходя из формулы:
![]()
![]() ,
где
,
где
![]() вероятность
нахождения
вероятность
нахождения
![]() фермионов
в k -том квантовом состоянии
фермионов
в k -том квантовом состоянии
23. Изменение
энтропии
![]() и
и
![]() для
процессов, изображенных на P-T диаграмме:
для
процессов, изображенных на P-T диаграмме:
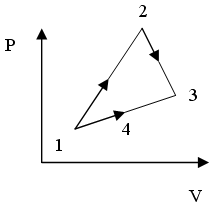
![]()
![]()
24.
![]() -плотность
вероятности или функция распределения
молекул идеального газа по модулю
скорости, для которой справедливо любое
соотношение, кроме:
-плотность
вероятности или функция распределения
молекул идеального газа по модулю
скорости, для которой справедливо любое
соотношение, кроме:
![]()

25. Распределение Больцмана по состояниям применимо при условии …
![]()
![]()
26. Если
![]() -
функции распределения по проекциям
скоростей для молекул идеального газа,
то:
-
функции распределения по проекциям
скоростей для молекул идеального газа,
то:
![]()
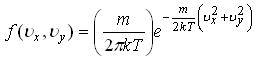
27. Распределение электронов по состояниям в зоне проводимости невырожденного полупроводника приведено на рис. ...
![]()
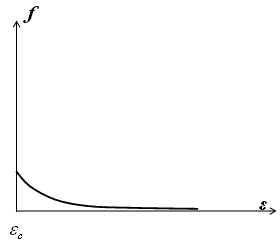
28. Для функции распределения Максвелла
по проекции импульса

29. Если F(x) – плотность вероятности или
функция распределения случайной величины
х, то выражение
 f(x)
f(x)
30. Если число
молекул идеального газа выросло в четыре
раза (N2=4N1),
а
![]() и
и
![]() ,
то относительное число молекул, имеющих
скорости от
,
то относительное число молекул, имеющих
скорости от
![]() до
до
![]() :
:
![]() осталось
прежним
осталось
прежним
31. Распределение Бозе-Эйнштейна по состояниям – это ...
![]() среднее
количество бозонов в одном квантовом
состоянии
среднее
количество бозонов в одном квантовом
состоянии
32. При увеличении температуры идеального
газа Т2=4Т1 отношение
максимальных значений функций
распределения по проекции скорости

33. Энергия Ферми металла
![]() эВ.
Эффективная масса электронов
эВ.
Эффективная масса электронов
![]() .
Максимальная скорость электронов при
Т=0 равна … км/с. Ответ округлить до
сотен.
.
Максимальная скорость электронов при
Т=0 равна … км/с. Ответ округлить до
сотен.
34. Формуле планка
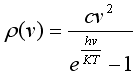 имеет
смысл ...
имеет
смысл ...
![]() Энергии
фотонов, находящихся в единичном малом
интервале частот
Энергии
фотонов, находящихся в единичном малом
интервале частот
35. В одновалентных металлах валентная зона заполнена …
![]() наполовину
наполовину
36. Распределение Больцмана по состояниям имеет вид ...
![]()
![]()
37. Температура
вырождения системы
![]() .
Для невырожденной системы выполняется
условие ...
.
Для невырожденной системы выполняется
условие ...
![]()
![]()
38. Формула
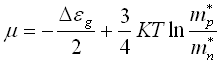 представляет
собой зависимость химического потенциала
от температуры для ...
представляет
собой зависимость химического потенциала
от температуры для ...
![]() примесного
полупроводника n–типа
примесного
полупроводника n–типа
40. Зависимость теплоёмкости твёрдого тела от температуры приведена на графикe …
![]()

41. Среднее количество электронов в
металле при T>0 в одном состоянии с
энергией
![]() равно
... Ответ записать в виде десятичной
дроби (округлить до десятых).
равно
... Ответ записать в виде десятичной
дроби (округлить до десятых).
42.
![]() -
соответственно: статистический вес,
энтропия, вероятность – связаны следующим
соотношением:
-
соответственно: статистический вес,
энтропия, вероятность – связаны следующим
соотношением:
![]()
![]()
![]()
![]()
43. Запишите формулу для количества
квантовых состояний, соответствующих
интервалу модуля скорости
![]() и
объему V, используя шаблон
и
объему V, используя шаблон
![]()
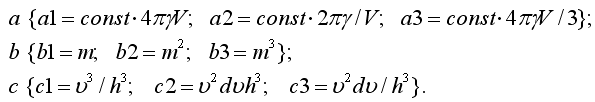
44. Необходимым и достаточным условием равновесного состояния системы является:
![]() замкнутость
системы и стационарность макропараметров
замкнутость
системы и стационарность макропараметров
45. Число возможных
состояний системы из N =100 квантовых
частиц (электронов) в конечном элементе
объема
![]() равно:
равно:
![]()
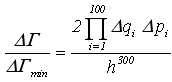
46. Химический потенциал фононов
![]()
47. Для молекул
идеального газа значения интегралов
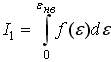 и
и
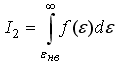 ,
где
,
где
![]() -
наиболее вероятная энергия:
-
наиболее вероятная энергия:
![]() I1<I2
I1<I2
48. Между свободной
и валентной зонами находится запрещённая
зона шириной
![]() Валентная
зона при
Валентная
зона при
![]() заполнена
на половину. Кристалл является . . .
заполнена
на половину. Кристалл является . . .
![]() проводником
проводником
49.На рисунке
изображена функция распределения
Ферми-Дирака по энергиям при разных
температурах.
 Кривая
1 соответствует Т1
Кривая 2 соответствует Т2
Кривая
1 соответствует Т1
Кривая 2 соответствует Т2
![]() Т1=0;
Т2>0
Т1=0;
Т2>0
50. Функция распределения Бозе-Эйнштейна по энергиям имеет вид ...
![]()

51. Найдите все возможные соответствия между левым и правым столбиками, если F(x) – плотность вероятности случайной величины х. Ответ дайте в виде: k-l, m-n, …
|
|
|
52. Изменение
энтропии
![]() при
плавлении льда (m-масса, λ -удельная
теплота плавления) равно:
при
плавлении льда (m-масса, λ -удельная
теплота плавления) равно:
![]()
![]()
53. Функция
распределения молекул идеального газа
по проекции скорости
![]() ,
пронормированная на 1, имеет вид:
,
пронормированная на 1, имеет вид:
![]()
54. Концентрация электронов в зоне проводимости собственного полупроводника возрастает с повышением Т за счёт перехода электронов
![]() из
валентной зоны в зону проводимости
из
валентной зоны в зону проводимости
55. Точка в фазовом пространстве для системы из N частиц характеризует:
![]() микросостояние
системы
микросостояние
системы
56. Одному квантовому состоянию (без учёта спина) соответствует фазовый объём …
![]()
![]()
57. Энергия Ферми – это …
![]() максимальная
энергия фермионов при Т=0
максимальная
энергия фермионов при Т=0
58. Распределение электронов по энергиям в зоне проводимости невырожденного полупроводника приведено на рис. ...
![]()

![]()
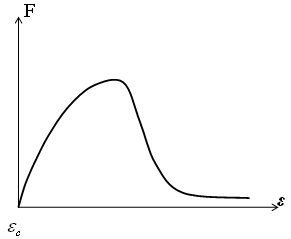
![]()

59. Если свойства системы частиц сильно зависят от квантовых свойств частиц, система является ...
![]() вырожденной
вырожденной
60. Найдите неправильное утверждение. Фазовое пространство для N независимых частиц можно:
![]() представить
как 3N-мерный
представить
как 3N-мерный
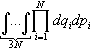 интеграл,
где qi={xi
yi
zi},
pi={pxi
pyi
pzi}
интеграл,
где qi={xi
yi
zi},
pi={pxi
pyi
pzi}
61. Перейти от
классической функции распределения по
модулю импульса
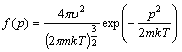 к
функции распределения по модулю скорости
f(u):
к
функции распределения по модулю скорости
f(u):
![]() можно,
заменив p на m
можно,
заменив p на m![]() и dp на mdu в выражении f(p)dp
и dp на mdu в выражении f(p)dp
62. Функция распределения Ферми-Дирака по модулю квазиимпульса равна …
![]()
![]()
63. Функция
распределения Бозе-Эйнштейна находится
путём усреднения по формуле
 ,
где K – это …
,
где K – это …
![]() набор
квантовых чисел, задающих данное
квантовое состояние свободного бозона
набор
квантовых чисел, задающих данное
квантовое состояние свободного бозона
64. Из приведенных величин: m –масса газа, S – энтропия, Т –температура, V –объем, Ω -статистический вес, n –концентрация частиц, p –давление - аддитивными являются:
![]() m,
S, V
m,
S, V
65.
![]() -
плотность вероятности
или функция распределения молекул
идеального газа по энергии. Заштрихованная
площадь равна:
-
плотность вероятности
или функция распределения молекул
идеального газа по энергии. Заштрихованная
площадь равна:

![]() относительному
числу молекул
относительному
числу молекул
![]() ,
имеющих энергию от
,
имеющих энергию от
![]() до
до
![]()
Если
![]() -
плотность вероятности или функция
распределения случайной величины х ( х
изменяется от - ∞ до + ∞), то справедливо
любое выражение, кроме:
-
плотность вероятности или функция
распределения случайной величины х ( х
изменяется от - ∞ до + ∞), то справедливо
любое выражение, кроме:
![]()
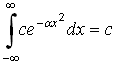
66. Для
![]() -
плотности вероятности или функции
распределения Максвелла по модулю
скорости, справедливо выражение:
-
плотности вероятности или функции
распределения Максвелла по модулю
скорости, справедливо выражение:
![]()
![]()
67. Функция
распределения молекул идеального газа
по модулю скорости
![]() (плотность
вероятности) имеет размерность:
(плотность
вероятности) имеет размерность:
![]()
![]()
68. Объем элементарной фазовой ячейки для одной квантовой частицы равен:
![]() h3
h3
69. Концентрация электронов собственного полупроводника зависит от температуры следующим образом …
![]()
![]()
70. Плотность квантовых состояний в энергетическом пространстве – это ...
![]() число
состояний в единичном малом интервале
энергии
число
состояний в единичном малом интервале
энергии
71. Для распределения
Ферми-Дирака по энергии выражение
 имеет
смысл …
имеет
смысл …
![]() общая
энергия всей системы фермионов
общая
энергия всей системы фермионов
72. На рисунке представлены распределения
Ферми-Дирака по состояниям для двух
систем частиц;
![]() ,
,
![]() .
Отношение масс частиц
.
Отношение масс частиц
![]() =
...
=
...

73. Для невырожденной
системы среднее количество частиц в
одном квантовом состоянии
![]() равно
равно
![]()
![]()
74.Газ из состояния
(1) переходит в состояние (2) в одном случае
по прямой 1-2 , а в другом – по линии
1-3-4-2. При этом изменение энтропии:

![]()
![]()
75. На рисунке
приведено распределение Ферми-Дирака
по энергиям. Площадь заштрихованной
области соответствует ...
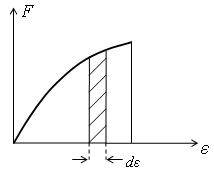
![]() числу
частиц, энергия которых находится в
интервале
числу
частиц, энергия которых находится в
интервале
![]()
76.
![]() если:
если:
![]() S=const
S=const
![]() p=const
p=const
![]() T=const
T=const
77. Для кристалла,
состоящего из N атомов
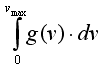 равен
равен
![]() 3N
3N
78. В функции
распределения Максвелла по проекции
скорости

![]() масса
одной молекулы определенного газа
масса
одной молекулы определенного газа
79. Плотность
вероятности или функция распределения
молекул идеального газа по проекции
скорости имеет вид
![]() ,
где нормированный множитель C равен:
,
где нормированный множитель C равен:
![]()
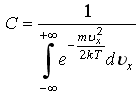
80. Правильным
соотношением для функции распределения
молекул идеального газа по проекции
импульса
 является:
является:
![]()

81. На рисунке
приведено распределение Ферми-Дирака.
 Каждое
состояние с энергией в интервале
Каждое
состояние с энергией в интервале
![]() заполнено
заполнено
![]() Частично
Частично
![]() Полностью
Полностью
![]() Наполовину
Наполовину
82.Энергетический спектр электронов в кристаллах . . .
![]() состоит
из разрешённых и запрещённых зон
одинаковой ширины
состоит
из разрешённых и запрещённых зон
одинаковой ширины
![]() состоит
из разрешённых и запрещённых зон
одинаковой ширины
состоит
из разрешённых и запрещённых зон
одинаковой ширины
![]() Полностью
Полностью
83. В равновесной
системе
![]()
![]() 0
0
84. При высоких
температурах
![]() теплопроводность
твердого тела зависит от температуры
по закону ...
теплопроводность
твердого тела зависит от температуры
по закону ...
![]()
![]() ,
т.к. энергия колебаний ∼T,
а количество возбуждённых мод не меняется
,
т.к. энергия колебаний ∼T,
а количество возбуждённых мод не меняется
85. Для получения полупроводника p-типа подбирают трехвалентную примесь, акцепторный уровень которой находится …
![]() в
запрещённой зоне вблизи потока валентной
зоны
в
запрещённой зоне вблизи потока валентной
зоны
86. Функция распределения Ферми-Дирака по энергиям имеет вид...
![]()
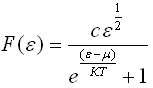
87. На рисунке
изображена функция распределения
Ферми-Дирака по модулю импульса при
разных температурах.
 Кривая
1 соответствует Т1
Кривая 2 соответствует Т2
Кривая
1 соответствует Т1
Кривая 2 соответствует Т2
![]() Т1=0;
Т2>0
Т1=0;
Т2>0
88.На рисунке
показано распределение Максвелла по
модулю скорости для некоторого газа
при разных температурах. При этом площади
под кривыми (Si)
и температуры (Тi)
удовлетворяют соотношению:

![]()
![]()
89. Основной постулат квантовой статистики - это ...
![]() принцип
тождественности частиц
принцип
тождественности частиц
90. Выражение
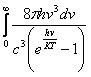 имеет
смысл ...
имеет
смысл ...
![]() энергии
фотонного газа в единице объёма
энергии
фотонного газа в единице объёма
91. Функция распределения Ферми-Дирака по состояниям – это …
![]() среднее
число фермионов в одном квантовом
состоянии
среднее
число фермионов в одном квантовом
состоянии
92. Распределение фононов по состояниям имеет вид:
![]()
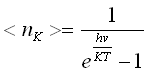
93. Для больших
частот
![]() спектральная
плотность энергии фотонного газа зависит
от частоты по закону ...
спектральная
плотность энергии фотонного газа зависит
от частоты по закону ...
![]()
![]()
![]()
94. Одному квантовому состоянию для N частиц (без учёта спина) соответствует фазовый объём …
![]() h3N
h3N
95. Функция распределения частиц по энергиям в квантовой статистике определяется по формуле …
![]()
![]()
96. Концентрация дырок в валентной зоне полупроводника p-типа в области низких температур увеличивается за счёт перехода электронов …
![]() из
валентой зоны в зону проводимости
из
валентой зоны в зону проводимости
97. Второе начало термодинамики утверждает, что в замкнутой системе:
![]() ΔS≥0
ΔS≥0
98. Функция распределения Ферми-Дирака по модулю импульса при Т=0 представлена на рисунке …
![]()
99. Термодинамическая система находится в равновесном состоянии, если:
![]()
![]()
100. Электроны, находящиеся в верхних разрешённых электрических зонах движутся . . .
![]() хаотически
по всему кристаллу в периодичном поле
всех ядер
хаотически
по всему кристаллу в периодичном поле
всех ядер
101. Реальные процессы в изолированных системах протекают:
![]() в
направлении увеличения хаотичности
движения частиц в системе
в
направлении увеличения хаотичности
движения частиц в системе
102. Отношение
электронной и решеточной теплоёмкостей
для твёрдого тела при высоких температурах
![]() составляет
…
составляет
…
![]()

103.
![]() -
плотность
вероятности или функция распределения
по проекции скорости для молекул
идеального газа принимает значения:
-
плотность
вероятности или функция распределения
по проекции скорости для молекул
идеального газа принимает значения:
![]()
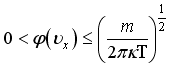
104. Энтропия неизолированной системы при необратимом теплообмене:
![]() только
увеличивается
только
увеличивается
![]() может
как и увеличиваться, так и уменьшаться
в зависимости от условий
может
как и увеличиваться, так и уменьшаться
в зависимости от условий
![]() только
уменьшается
только
уменьшается
![]() не
изменяется
не
изменяется
105. Среднее значение
![]() для
одноатомного идеального газа можно
рассчитать, пользуясь любым выражением,
кроме …
для
одноатомного идеального газа можно
рассчитать, пользуясь любым выражением,
кроме …
![]()
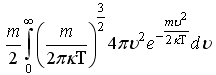
106. Изменение
энтропии при переходе из состояния (1)
в состояние (2):

![]()
![]()
![]()
![]()
![]()
![]() нельзя
определить, так как неизвестно соотношение
температур
нельзя
определить, так как неизвестно соотношение
температур
![]()
![]()
107. Если х - случайная
физическая величина, принимающая ряд
дискретных значений х1,
х2,
…хп,
а Рi
– вероятность появления xi,
то среднее значение
![]() равно:
равно:
![]()

108. Длина волны де
Бойля
![]() ,
среднее расстояние между частицами l.
Для невырожденной системы выполняется
условие ...
,
среднее расстояние между частицами l.
Для невырожденной системы выполняется
условие ...
![]()
![]()
109.Распределение
Максвелла-Больцмана для идеального
газа имеет вид:

![]() потенциальная
энергия частиц во внешнем поле плюс
суммарная кинетическая энергия молекул
потенциальная
энергия частиц во внешнем поле плюс
суммарная кинетическая энергия молекул
110. Одному квантовому состоянию для одной частицы в трехмерном пространстве соответствует фазовый объем
![]()
![]()
111. Каноническое
распределение Гиббса имеет вид
![]() ,
где постоянная С равна :
,
где постоянная С равна :
![]()

112. Если F(x) –
плотность вероятности или функция
распределения случайной величины х, то
выражение
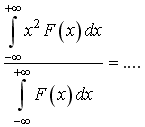
![]()
![]()
113.
![]() -плотности
вероятности или функции распределения
молекул по проекциям скорости, для
которых справедливо любое соотношение,
кроме…
-плотности
вероятности или функции распределения
молекул по проекциям скорости, для
которых справедливо любое соотношение,
кроме…
![]()

114. Условием нормировки функции распределения Максвелла по модулю скорости для молекул идеального газа является выражение:
![]()

115. Концентрация электронов в зоне проводимости примесного проводника n-типа в области низких температур увеличивается за счёт перехода электронов …
![]() с
донорного уровня в зону проводимости
с
донорного уровня в зону проводимости
![]() с
донорного уровня в зону проводимости
с
донорного уровня в зону проводимости
116.
![]() -плотность
вероятности или функция распределения
случайной величины х, Нормированный
множитель С равен:
-плотность
вероятности или функция распределения
случайной величины х, Нормированный
множитель С равен:
![]()
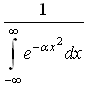
117. Носителями тока в собственном полупроводнике являются …
электроны на донорных уровнях и дырки в валентной зоне
![]() только
дырки в валентной зоне
только
дырки в валентной зоне
![]() электроны
в зоне проводимости и дырки в валентной
зоне
электроны
в зоне проводимости и дырки в валентной
зоне
118. При T=const максимальное значение функции распределения по проекции импульса f(px):
![]()
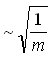
119. Основной постулат квантовой статистики (принцип тождественности) является следствием того, что ...
![]() описание
движения отдельной частицы носит
вероятностный характер
описание
движения отдельной частицы носит
вероятностный характер
120. Случайная
величина х принимает значения от 0 +∞.
Функция распределения случайной величины
х или плотность вероятности имеет вид
![]() ,
где нормировочный множитель С равен:
,
где нормировочный множитель С равен:
![]() b
b
121. Зонный характер энергетического спектра электронов в кристаллах связан с . . .
![]() перекрытием
волновых функций электронов из соседних
атомов
перекрытием
волновых функций электронов из соседних
атомов
122.На рисунке
приведено распределение Бозе-Эйнштейна
для двух температур. Соотношение
температур T2
… T1.
 Для
кривых выполняется соотношение:
Для
кривых выполняется соотношение:
![]()
![]()
123.Ширина разрешенной
энергетической зоны
![]() в
одновалентном кристалле имеется N=1022
атомов. Расстояние между соседними
подуровнями в зоне равно
в
одновалентном кристалле имеется N=1022
атомов. Расстояние между соседними
подуровнями в зоне равно
![]()
![]()
124. Для классической
функции распределения по модулю скорости
при условии Т=const, а u2>u1
отношение
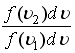
![]() всегда
>1
всегда
>1
![]() >1,
если υ1<υнв<υ2
>1,
если υ1<υнв<υ2
![]() <1,
если υ1
и υ2
меньшеυнв
<1,
если υ1
и υ2
меньшеυнв
![]() >1,
если υ1
и υ2
меньшеυнВ
>1,
если υ1
и υ2
меньшеυнВ
![]() <1,
если υ1
и υ2
большеυнв
<1,
если υ1
и υ2
большеυнв
125. У изолированной системы, находящейся в равновесном состоянии:
![]() E
= Emin
E
= Emin
![]() Ω=Ωmin
Ω=Ωmin
126. f(x2)
– некоторая функция случайной величины
x. Интеграл
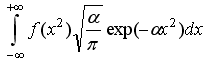 равен:
равен:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
127. Если
![]() -
плотность вероятности или функция
распределения молекул идеального газа
по энергии, то среднее значение
-
плотность вероятности или функция
распределения молекул идеального газа
по энергии, то среднее значение
![]() на
интервале энергий от
на
интервале энергий от
![]() до
до
![]() равно:
равно:
![]()
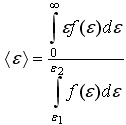
128. Функция распределения по энергии в квантовой статистике – это
![]() плотность
вероятности нахождения частицы в
интервале
плотность
вероятности нахождения частицы в
интервале
![]()
![]() вероятность
нахождения частицы с энергией
вероятность
нахождения частицы с энергией
![]()
![]() среднее
число частиц с энергией
среднее
число частиц с энергией
![]()
![]() среднее
число частиц в единичном малом интервале
энергии
среднее
число частиц в единичном малом интервале
энергии
129. При стремлении изолированной системы к равновесному состоянию:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
130. Функция распределения Ферми-Дирака по состояниям имеет вид …
![]()

131. Для N квантовых частиц объем минимальной фазовой ячейки, приходящейся на одно квантовое микросостояние системы, ΔГmin равен:
![]() h3N
h3N
132. Для циклического
процесса, изображенного на рис:
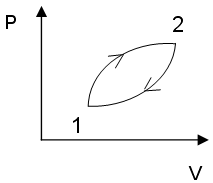
![]()
![]()
133. Длина волны де
Бойля
![]() ,
среднее расстояние между частицами l.
Для невырожденной системы выполняется
условие ...
,
среднее расстояние между частицами l.
Для невырожденной системы выполняется
условие ...
![]()
![]()
134. Для электронов в зоне проводимости невырожденного полупроводника следует применить распределение … Укажите все возможные варианты.
![]() Максвелла
Максвелла
![]() Ферми-Дирака
Ферми-Дирака
135. Функция
распределения Ферми-Дирака по состояниям
находится по формуле
 ,
где k – это ...
,
где k – это ...
![]() Набор
квантовых чисел, задающих квантовое
состояние частицы в атоме
Набор
квантовых чисел, задающих квантовое
состояние частицы в атоме
136. В замкнутой
системе энтропия может меняться со
временем, как показано на участках:
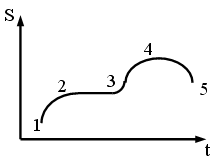
![]() 2-3-4
2-3-4
![]() 4-5
4-5
![]() 1-2-3-4
1-2-3-4
![]() 1-2-3
1-2-3
137. Для электронного
газа в металле
 имеет
смысл
имеет
смысл
![]() количества
электронов в зоне проводимости
количества
электронов в зоне проводимости
138. Теплоёмкость электронного газа в металлах …
![]()
![]() т.к.
средняя энергия теплового движения
электронов в металле
т.к.
средняя энергия теплового движения
электронов в металле
![]()
139. Функция распределения Бозе-Эйнштейна по состояниям может быть получена путём усреднения по формуле ...
![]()
![]() ,
где
,
где
![]() -
то же, что и в пункте А
-
то же, что и в пункте А
140. На рисунке
приведены графики изохоры, изобары,
изотермы, адиабаты. Правильные названия
графиков:
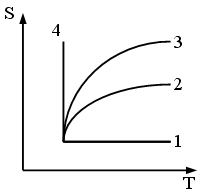
![]() 1-адиабата,
2-изохора, 3-изобара, 4-изотерма
1-адиабата,
2-изохора, 3-изобара, 4-изотерма
141. Если
![]() –
функция распределения молекул идеального
газа по проекции скорости, то для
интегралов:
–
функция распределения молекул идеального
газа по проекции скорости, то для
интегралов:
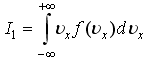 ,
,
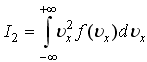 ,
,
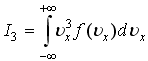 справедливо
следующее соотношение:
справедливо
следующее соотношение:
![]()
![]()
142. Для малых частот
![]() спектральная
плотность энергии фотонного газа зависит
от частоты по закону . . .
спектральная
плотность энергии фотонного газа зависит
от частоты по закону . . .
![]()
![]()
![]()
143. Энергия квантового гармонического осциллятора равна
![]()
![]()
144. Средние скорости
молекул идеальных газов, у которых
![]() ,
а массы молекул
,
а массы молекул
![]()
![]()
![]()
145. Система фононов описывается статистикой
![]() Бозе-Эйнштейна
Бозе-Эйнштейна
146. Выражение

![]() равно
вероятности встретить подсистему,
состоящую из N частиц, в состоянии с
энергией εi
равно
вероятности встретить подсистему,
состоящую из N частиц, в состоянии с
энергией εi
147. Функция распределения Ферми-Дирака по энергиям при Т=0 представлена на рисунке...
![]()

148. Число доступных
состояний в элементе фазового пространства
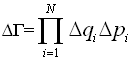 для
классической частицы:
для
классической частицы:
![]() →
∞
→
∞
149. Концентрация дырок в валентной зоне собственного полупроводника зависит от температуры следующим образом:
![]()
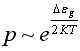
![]()

150. При низких
температурах
![]() теплоёмкость
твёрдого тела зависит от температуры
по закону
теплоёмкость
твёрдого тела зависит от температуры
по закону
![]()
![]() ,
т.к. новые моды упругих колебаний
оказываются возбуждёнными
,
т.к. новые моды упругих колебаний
оказываются возбуждёнными
151. Число доступных микросостояний в некотором фазовом объеме ΔГ:
![]() одинаково
для классической и квантовой частицы
одинаково
для классической и квантовой частицы
![]() конечно
для классической частицы, т.к. она имеет
определенные размеры
конечно
для классической частицы, т.к. она имеет
определенные размеры
![]() бесконечно
для квантовой частицы, т.к. ее размерами
можно пренебречь
бесконечно
для квантовой частицы, т.к. ее размерами
можно пренебречь
![]() бесконечно
для классической частицы, т.к. в каждый
момент времени объем, который в фазовом
пространстве определяет ее состояние,
стремится к нулю
бесконечно
для классической частицы, т.к. в каждый
момент времени объем, который в фазовом
пространстве определяет ее состояние,
стремится к нулю
152. В модели Эйнштейна - Дебая постулируется, что N атомов кристалла должны иметь ...
![]() 3N
колебательных мод с одинаковой фазовой
скоростью
3N
колебательных мод с одинаковой фазовой
скоростью
153. В термодинамической системе при необратимом процессе:
![]()

![]()
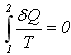
154. Функция распределения Максвелла по модулю скорости (плотность вероятности) f(υ) равна:
![]() относительному
числу молекул в единичном интервале
скоростей
относительному
числу молекул в единичном интервале
скоростей
155. Вероятность Р наступления любого из двух независимых событий А или В равна:
![]() сумме
вероятностей Р(А)+Р(В)
сумме
вероятностей Р(А)+Р(В)
156.Правильным
рисунком функций плотности вероятности
f(v) для одинаковых газов, у которых
![]() ,
давление не меняется, а
,
давление не меняется, а
![]() ,
является:
,
является:
![]()
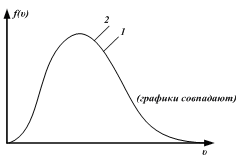
157. Изменение энтропии идеального газа в результате адиабатного расширения:
![]()
![]()
![]() для
однозначного ответа необходимо знать,
квазиравновесный процесс или нет
для
однозначного ответа необходимо знать,
квазиравновесный процесс или нет
![]()
![]()
158. Для получения полупроводника n-типа подбирают пятивалентную примесь, донорный уровень которой находится ...
![]() в
запрещённой зоне вблизи дна зоны
проводимости
в
запрещённой зоне вблизи дна зоны
проводимости
159. Между свободной
и валентной зонами находится запрещённая
зона шириной
![]() Валентная
зона при
Валентная
зона при
![]() заполнена
полностью. Кристалл является . . .
заполнена
полностью. Кристалл является . . .
![]() изолятором
изолятором
![]() проводником
или полупроводником в зависимости от
температуре
проводником
или полупроводником в зависимости от
температуре
160. Принцип Паули утверждает, что ...
![]() в
одном квантовом состоянии может
находиться не более одного фермиона
в
одном квантовом состоянии может
находиться не более одного фермиона
161. Распределение Максвелла по модулю скорости для некоторого идеального газа при Т1>Т2 показано на рисунке:
![]()
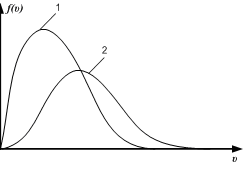
![]()

![]()

162. Если F(х) – плотность вероятности случайной величины х, то F(x)dx):
![]() Принимает
значения больше 0, но меньше 1
Принимает
значения больше 0, но меньше 1
163. Функции распределения по проекции импульса рх (плотность вероятности) для разных газов, у которых m2>m1, а T1=T2, показаны на рисунке:
![]()

164. Изменение
энтропии при изотермическом квазиравновесном
процессе 1-2:
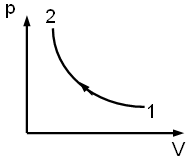
![]() ΔS12
= 0
ΔS12
= 0
165. Наиболее
вероятное значение проекции скорости
![]() для
молекул идеального газа равно:
для
молекул идеального газа равно:
![]() 0
0
166. Распределение Бозе-Эйнштейна по энергиям – это …
![]() среднее
число бозонов в единичном малом интервале
энергии
среднее
число бозонов в единичном малом интервале
энергии
168. Если функция
распределения по энергии для молекул
идеального газа пронормирована на число
частиц
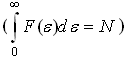 ,
то интеграл
,
то интеграл
 равен:
равен:
![]() суммарной
энергии всех частиц, у которых
суммарной
энергии всех частиц, у которых
![]()
169. На рисунке
приведено распределение Ферми-Дирака.
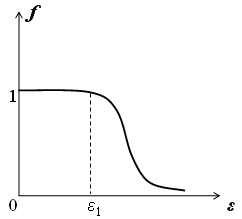 Состояния
с энергиями в интервале
Состояния
с энергиями в интервале
![]() заполнены
...
заполнены
...
![]() полностью,
в каждом находится один фермион
полностью,
в каждом находится один фермион
170. Отношение теплоёмкости вырожденного электронного газа и теплоёмкости не вырожденного классического газа равно:
![]()
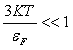
171. На
рисунке приведено распределение

![]() Ферми-Дирака
по состояниям при
Ферми-Дирака
по состояниям при
![]()
172. Для невырожденного полупроводника функция распределения электронов по энергиям в зоне проводимости имеет вид…
![]()
![]()
173. Согласно
теореме о равнораспределении энергии
по степеням свободы
![]() равно:
равно:
![]()
![]()
![]()
![]()
174. В замкнутой системе при необратимых процессах, если N=const:
![]() dE<TdS-pdV
dE<TdS-pdV
175.При увеличении температуры основная причина роста электропроводности собственного полупроводника …
![]() увеличение
концентрации носителей тока
увеличение
концентрации носителей тока
176. Функция распределения частиц по энергиям в квантовой статистике – это …
![]() среднее
число частиц с энергией
среднее
число частиц с энергией
![]()
![]() среднее
число частиц в одном квантовом состоянии
с энергией
среднее
число частиц в одном квантовом состоянии
с энергией
![]()
![]() среднее
число частиц в малом единичном интервале
энергии
среднее
число частиц в малом единичном интервале
энергии
![]() вероятность
нахождения частицы с энергией
вероятность
нахождения частицы с энергией
![]()
177. Если х - случайная физическая величина, принимающая ряд дискретных значений х1,х2, … хn, а Рi – вероятность появления хi, то < x2 > равно:
![]()
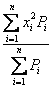
![]()
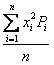
178. Изображенный
циклический процесс:

![]() необратимый,
квазиравновесный
необратимый,
квазиравновесный
179. Уравнение состояния идеального газа имеет вид:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
180. Вероятность Р одновременного наблюдения 2-х независимых событий А и В равна:
![]() наибольшей
из 2-х вероятностей
наибольшей
из 2-х вероятностей
![]() сумме
вероятностей Р(А)+Р(В)
сумме
вероятностей Р(А)+Р(В)
![]() произведению
вероятностей Р(А)•Р(В)
произведению
вероятностей Р(А)•Р(В)
181. Функции
распределения по энергии
![]() для
некоторого газа при Т2>Т1
показаны на рисунке:
для
некоторого газа при Т2>Т1
показаны на рисунке:
![]()

![]()
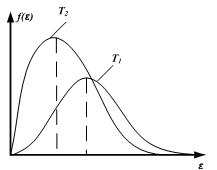
![]()
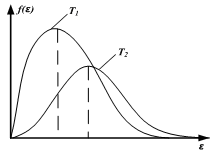
182. Среднее значение
![]() можно
найти, пользуясь любым выражением,
кроме…
можно
найти, пользуясь любым выражением,
кроме…
![]()
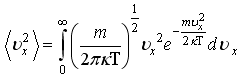
184. На рисунке
приведены распределения
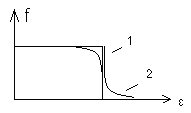
![]() Ферми-Дирака
по состояниям, кривая 1 соответствует
Т=0, кривая 2 – Т>0
Ферми-Дирака
по состояниям, кривая 1 соответствует
Т=0, кривая 2 – Т>0
185. Фазовая траектория для системы из N частиц показывает:
![]() изменение
микросостояния системы
изменение
микросостояния системы
186. f(p)- функция
распределения по модулю импульса для
молекул идеального газа. Среднее значение
![]() равно:
равно:
![]()

![]()
![]()
187. Для функций
распределения
 и
и
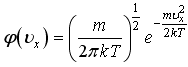 справедливо
соотношение:
справедливо
соотношение:
![]()
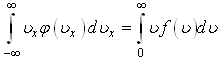
![]()

188. В кристаллическом
натрии электрон в состоянии 1S находится
в поле действия ядра в среднем
![]() Ширина
соответствующей уровню 1S энергетической
зоны равна … .
Ширина
соответствующей уровню 1S энергетической
зоны равна … .
![]() .
.
![]()
![]()
189. Статистический вес:
![]() зависит
от числа частиц системы и не зависит от
её энергии
зависит
от числа частиц системы и не зависит от
её энергии
![]() прямо
пропорционален вероятности состояния
системы
прямо
пропорционален вероятности состояния
системы
190. Неправильным утверждением является. Вероятность случайного события Р:
![]() Р
изменяется от 0 до ∞
Р
изменяется от 0 до ∞
191.
![]() если:
если:
![]() p=const
p=const
![]() T=const
T=const
![]() S=const
S=const
192. Распределение
Больцмана
![]() применимо
для ...
применимо
для ...
![]() систем
частиц малой плотности, у которых не
проявляются квантовые свойства
систем
частиц малой плотности, у которых не
проявляются квантовые свойства
193. Теплоемкость общей массы идеального одноатомного газа при V=const:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
194. Размерность статистического веса:
![]() безразмерная
величина
безразмерная
величина
![]()
![]()
195. Химический
потенциал системы бозонов
![]()
![]()
![]()
196. Если F(x) – функция
распределения случайной величины х, а
f(x2)
– некоторая функция этой величины, то
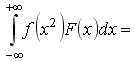
![]()
![]()
197. Если электронный газ находится в невырожденном состоянии, график функции распределения по состояниям имеет вид:
![]()
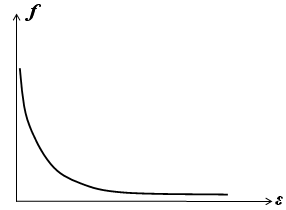
198.
![]() -
плотность вероятности или функция
распределения молекул идеального газа
по модулю скорости, для которой справедливо
любое соотношение, кроме:
-
плотность вероятности или функция
распределения молекул идеального газа
по модулю скорости, для которой справедливо
любое соотношение, кроме:
![]()
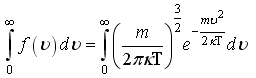
199. Наиболее вероятное значение энергии для молекул идеального газа:
![]() не
зависит от
не
зависит от
![]()
200. F(x) – плотность
вероятности или функция распределения
случайной величины х. Среднее значение
![]() на
интервале от х1
до х2
равно:
на
интервале от х1
до х2
равно:
![]()
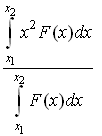
201. Статический вес системы:
![]() зависит
от числа частиц системы
зависит
от числа частиц системы
202.
 -
функция распределения
молекул идеального газа по энергии,
которая удовлетворяет любому соотношению,
кроме:
-
функция распределения
молекул идеального газа по энергии,
которая удовлетворяет любому соотношению,
кроме:
![]()
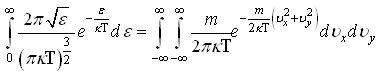
![]()
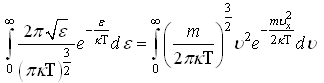
![]()

![]()
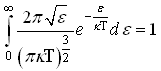
203. Выражение
 равно:
равно:
![]() 1
1
![]() среднему
значению
среднему
значению
![]()
![]() 0
0
![]() среднему
значению
среднему
значению
![]()
204. Для распределения
Ферми-Дирака по энергии выражение
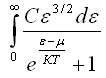 имеет
смысл …
имеет
смысл …
![]() общая
энергия всей системы фермионов
общая
энергия всей системы фермионов
205. Температура
абсолютного черного тела равна Т=103
К. Постоянная в законе смещения Вина
 .
Максимум спектральной плотности
излучения находится при частоте
.
Максимум спектральной плотности
излучения находится при частоте
![]()
![]()
206. Молекулы идеального газа :
![]() могут
иметь как целый, так и полу целый спин
могут
иметь как целый, так и полу целый спин
207. F(x)
– плотность вероятности или функция
распределения случайной величины х.
Среднее значение
![]() равно:
равно:
![]()
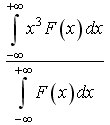
208. Изолированный сосуд разделен перегородкой на две половины. В одной находится газ, другая пустая. Перегородку убирают и дожидаются установления равновесия. При этом в системе:
![]() энтропия
увеличивается, а средняя энергия каждой
частицы не изменяется
энтропия
увеличивается, а средняя энергия каждой
частицы не изменяется
209. При одинаковых температурах наиболее вероятная скорость молекул кислорода ……… наиболее вероятной скорости молекул водорода. Вставьте слово.РАВНА
210. При Т=0 химический потенциал собственного полупроводника μ= –0,5 эВ. Ширина запрещенной зоны рана … эВ.
1
211. Запишите формулу для
плотности состояний, используя шаблон
![]()

![]()
![]()
dE=μdN если: нет правильного ответа
dE=-δA+µdN: S=const
![]() - функ распред:
- функ распред:
![]() F(v)-
плотность вероят по модулю скор,:
F(v)-
плотность вероят по модулю скор,:
![]() -
плот вероят по эн. <E>:
-
плот вероят по эн. <E>:
![]()
-
распред идеал газа по энерг.=
F(x)=Ce-ax2-
плотность вероятности Нормир множитель
С :
![]()
![]() -
плотность вероят по проек скорости :
-
плотность вероят по проек скорости :
![]()
f(p)-
функция распределения по модулю импульса
: ![]()
f(E)-
плот вероят идеал газа по эн.
![]() отност
числу dN/N,
им эн от E1
до
E1+dE
F(x)
– плот вероят или фун распред случ велич
х. Сред ч
отност
числу dN/N,
им эн от E1
до
E1+dE
F(x)
– плот вероят или фун распред случ велич
х. Сред ч ![]() :
:
![]()
F(x) –
плот вероят или случ вел х. Сред ![]() на инт х1
до х2
:
на инт х1
до х2
: ![]()
![]() п пр скор,…
п пр скор,…
![]()
![]() -
это средняя
квадрат скор, где m
– масса одной молекулы
-
это средняя
квадрат скор, где m
– масса одной молекулы
f(x2)
некот фун вел x. нтеграл![]() :
: ![]()
Выраж
![]() ... энергии
фотонного газа в единице объёма
... энергии
фотонного газа в единице объёма
Выражение
![]() равно:
0
равно:
0
Выраж
 равно
вероят подсис, состиз N част, в сост с эн
εi
равно
вероят подсис, состиз N част, в сост с эн
εi
Вероят Р наступ из двух независ А или В равна: сумме вероят Р(А)+Р(В)
Вероят Р одноврем наблюд 2-х соб А и В равна: произв вероят Р(А)•Р(В)
В функции распределения Максвелла по проекции скорости
![]()
В
термодинамической системе при необрат
процессе: ![]()
В интер ε,ε+dε …dΩ, число частиц dN. Для невыр сист dN<<dΩ
В
кристалл натрии …![]()
![]() .
.
Вероятность достоверного события равна ….Ответ: 1
Второе начало
термодинамики утверждает, что в замк
сист: ![]()
В равновесной
системе ![]() =0
=0
В мод Эйн - Деб N атомов ... 3N колебат мод с один фазовой скор
В замкн сист
энтропия мен со врем, как показ на
участках:
![]() 1-2-3
В
одновалентных металлах валентная зона
заполнена … наполовину
1-2-3
В
одновалентных металлах валентная зона
заполнена … наполовину
Графики
1,2,3 распред Максвелла по модулю импульса
…![]() 1
Газ из сост (1) перех в сост (2) в одном
случае по прям 1-2 , а в др –
1
Газ из сост (1) перех в сост (2) в одном
случае по прям 1-2 , а в др –
по лин
1-3-4-2. изменение энтропии:
![]()
![]() Для
циклического процесса, изобр на рис:
Для
циклического процесса, изобр на рис:
![]()
![]() Для
распред Ф-Дир по эн
Для
распред Ф-Дир по эн ![]() число
част в интер
число
част в интер ![]()
Для распред Ф-Дир
по эн ![]() общая
энерг всей сист фермионов
общая
энерг всей сист фермионов
Для электронов в
зоне провод невырожд полупровод
Максвелла;
Ф-Дир
Для
кристалла, состоящего из N атомов![]() равен 3N
равен 3N
Для получения п/п n-типа… донор уров в запрещ зоне вблизи дна зоны провод
Для
равн 2х подсист замк системы равны: ![]()
Для получ п/п p-типа акцепт уров в запрещ зоне вблизи пот вален зоны
Для молI1= и I2= Eнв- наиб вероятная энерг I1<I2
Для эл газа в
металле ![]() количес
электрон в зоне провод
количес
электрон в зоне провод
Для клас функ по
мод скор Т=const, а u2>u1
![]()
Для
невыр п/п функ по эн в з проводимости
![]()
Для получ п/п p-типа акцеп уров в запрещ зоне вблизи потока вал зоны
Для мал частот kT>>hv спек плот эн фот газа. . . p=cv2 Для f(v)- плот вер Максвелла по мод скор выражение: 0<f(v)dv<1
Для
функ распр ![]() и
и
![]()
справедливо
соотношение: ![]()
Длина волны де Бойля . Для невырож систе условие ...
Для N квант част объем миним фазовой ячейки, ΔГmin : h3N
Для
невыр сист сред кол част в одном квант
сост <nk>
![]()
Если
![]() и
φ
и
φ![]() по проек скор
по проек скор ![]()
Если свойства системы частиц…, система является вырожденной
Если
х - случ физ велич х1,
х2,
…хп,
а Рi
– xi,сред
з ![]() :
:![]()
Если
х - случ физ велич х1,х2,
… хn,
а Рi
–хi,
то < x2
>
: ![]()
Если
функ распред по эн (![]() )
,
)
,
![]() :
:
суммарной
энергии всех частиц, у которых ![]()
Если
F(x) – плот вероят случ вел х, то выраж
![]()
Если
![]() функ рас по скор:
функ рас по скор:
![]()
Если
F(x)=Ce-ax2
- плот вероят случ х ( х изм от - ∞ до +
∞): ![]()
Если
f(vx)–
функ распредпо пр скор, :![]() ;
;
![]()
![]() :
I1=I3=0;I2>0
:
I1=I3=0;I2>0
Если
F(x) – функ распред х, а f(x2)
– некот ф ![]()
Если F(х) – плот вероят х, то F(x)dx): Приним знач бол 0, но мен 1
Если
чис мол (N2=4N1),
а ![]() и
и![]() от v
до
v+dv:
остал
преж
от v
до
v+dv:
остал
преж
Если
F(x) – плотность вероятности х, то ![]() 1
Если
f(E)-
плотность вероятности по эн, <E>
от E1
до
E2:
1
Если
f(E)-
плотность вероятности по эн, <E>
от E1
до
E2:
![]()
Зонный характер энергетич спектра электр в кристаллах
перекрытием волн функций электронов из соседних атомов
Значения интегралов
![]() (
(![]() при
одинаковых темп:
при
одинаковых темп:
нельзя сравн, так как знач интеграла зав от выбран интервала скор
Завис
теплоём твёрдого тела от темпры приведена
на граф
![]()
Из привед вел: m –, S – , Т –, V –, Ω -стат вес, n –концен част, p –явл: m, S, V
Измен
энтр ![]() при
плавлении льда (m-масса, λ -удел)
:
при
плавлении льда (m-масса, λ -удел)
: ![]()
Изображ
циклич:
![]() необратимый, квазиравновесный
Изменение
энтропии при изотермическом квазиравновесном
1-2:
необратимый, квазиравновесный
Изменение
энтропии при изотермическом квазиравновесном
1-2:
![]() ΔS12
= 0
Изменение
энтропии при пер из (1) в (2):
ΔS12
= 0
Изменение
энтропии при пер из (1) в (2):
![]()
![]() Изменение
энтропии
Изменение
энтропии ![]() и
и
![]() ,
изоб на P-T диаг:
,
изоб на P-T диаг:
![]()
![]() Изменение
энтропии адиабатного расшир:
для
однознач ответа
Изменение
энтропии адиабатного расшир:
для
однознач ответа
необходимо знать, квазиравновесный процесс или нет
Изолиров сосуд разделен перег на две полы. :
энтропия увеличивается, а средняя эн каждой частицы не изм
Концентрация электронов в зоне пров прим проводника n-типа
в обл низких темп увел донорного уровня в зону проводимости
Концентрация дырок в валентной зоне полупроводника p-типа
из валентной зоны на акцепторный уровень
Каноническое
распределение Гиббса ![]() ,
,
![]()
Концентр электрв в зоне пров собств п/п возр с повыш Т из вал зы в зону пров
Каждому типу п/п энерг диаг собствен(Ec Ev)прим N(Ec ED Ev) прим Р(Ec Eа Ev)
Концентр
дырок в вал зоне собств п/п зависит от
темп: ![]()
Концентрация
электронов собственного п/п зависит от
темп ![]()
Между
своб и вал ![]() Вал T=0.
Кристалл явл
изолятором
Вал T=0.
Кристалл явл
изолятором
Между
своб и вал зон ![]() Вал з Т=0
з
Кристалл яв.
проводником
Вал з Т=0
з
Кристалл яв.
проводником
Молекулы идеального газа : могут иметь как целый, так и полу целый спин
На
рис привед граф из, изоб, изот, ад:
![]() 1-ади,
2-изох, 3-изоб, 4-изот
1-ади,
2-изох, 3-изоб, 4-изот
На рис показ распр
Максве по мод скор (Si)
и (Тi)
:
![]() S1=
S2=
S3=1,Т3>
Т2>
Т1
На
рис приведено распр Бо-Эйн для двух
температур. T2
… T1.
S1=
S2=
S3=1,Т3>
Т2>
Т1
На
рис приведено распр Бо-Эйн для двух
температур. T2
… T1.
![]() Т1<<
Т2
На
рис прив распр Фе-Дир по эн.
Т1<<
Т2
На
рис прив распр Фе-Дир по эн.
![]() чис част, эн которых наход в инт E;E+dE
На
рис привед распр Фе-Дир.
чис част, эн которых наход в инт E;E+dE
На
рис привед распр Фе-Дир.
![]()
![]() полн,
в каж наход один фермион
На
рис привед распред
полн,
в каж наход один фермион
На
рис привед распред
![]() Фе-Дир по сост, кр 1 соот Т=0, кр 2 – Т>0
На
рис изобр функ распр Фе-Дир по мод имп.
Фе-Дир по сост, кр 1 соот Т=0, кр 2 – Т>0
На
рис изобр функ распр Фе-Дир по мод имп.
![]() Т1=0;
Т2>0
На
рис изобр функ распр Фе-Дир по эн.
Т1=0;
Т2>0
На
рис изобр функ распр Фе-Дир по эн.
![]() Т1=0;
Т2>0
На
рис приведено распределение
Т1=0;
Т2>0
На
рис приведено распределение
![]() Фе-Дир по сост при T=0
На
рис приведено распределение Фе-Дир.
Интервал эн E1<E<E2
Фе-Дир по сост при T=0
На
рис приведено распределение Фе-Дир.
Интервал эн E1<E<E2
![]() 2KT
На
рис приведено распр Фе-Дир.
2KT
На
рис приведено распр Фе-Дир.
![]() E1<E<E2
заполнено
Частично
Найдите
неправил утвер. Фаз прост для N:
представить
как
E1<E<E2
заполнено
Частично
Найдите
неправил утвер. Фаз прост для N:
представить
как
3N-мерный
![]() интеграл, где qi={xi
yi
zi},
pi={pxi
pyi
pzi}
интеграл, где qi={xi
yi
zi},
pi={pxi
pyi
pzi}
Неправильным утвержд явл. Вероят случ события Р: Р изменяется от 0 до ∞
Носителями тока в собств п/п явл электроны в з провод и дырки в вал зоне
Наиболее вероятное значение проекции скорости vx для молекул: 0
Наиболее вероятное значение эн для молекул: не зависит от m
Необход и достаточ услов равнов сост сист: замкн сист и стацион макроп
Найдите соответс между назван велич из лев столбика и их аналитич
выраж
из прав. k-l, m-n, средняя
квадратичная флуктуация(![]() );
);
среднее значение флуктуации(<(x-<x>)>); средний квадрат флуктуации
(дисперсия)(<(x2)>-(<x>)2);
относительная флуктуация(![]() )
)
Отношение колич атомов в двух кристал N2/N1=8, отн темп Деб T2/T1=.2
Основное
термодинамическое равенство :![]()
Отношение
макс знач функ распр ![]() .
вероят знач
.
вероят знач ![]() 4
4
Основной постулат квантовой статистики - принцип тождествен частиц
Основной постулат квантовой статист (принцип тождественности)
описание движения отдельной частицы носит вероятностный характер
Объем элементарной фазовой ячейки для одной квантовой: h3
Отношение теплоёмкости вырожденного эле газа и теплоём :
Одному квантовому состоянию (без учёта спина) Гmin=h3
Одному квантовому состоянию для одной частицы Гmin=h3
Отношение элект и реш тепло для твёр т высок темп Т>>ТДебая
Одному квантовому состоянию для N частиц (без учёта спина) h3N
При
стремлении изолированной системы к ![]()
Плотность квантовых состояний в энергетическом пространстве
число состояний в единичном малом интервале энергии
При низк темп
Т<<ТДебая
![]()
При выс темп Т>>ТДебая C=const, т.к. эн колеба кол возбуж мод не мен
При
T=const макс значфун распр по проек импульса
f(px):
![]()
Правил соот ![]() :
: ![]()
Принцип Паули в одном квант … наход не более одного фермиона
Перейти от класс фун распределения по моду скор имп
![]() к
функ распр по эн f(e)
к
функ распр по эн f(e)
можно,
заменив ![]() на
на
![]() и
dv
на
и
dv
на
![]() в
выражении f(v)dv
в
выражении f(v)dv
Перейти
от клас фун распр по мод имп ![]()
f(u): можно, заменив p на m v и dp на mdu в выражении f(p)dp
При увел темп основ прич роста электропроводности собств п/п
увеличение концентрации носителей тока
При конденсации пара энтропия системы: уменьшается
При равнов тепловом излуч тело излуч и поглощает кол эни за одно и
то же время с одной и той же площади интервале частот dν
Пучок электронов дает дифракционную картину от кристалла:
получится точно такой же, если число элект в обоих эксп будет один
При Т=const макс знач плотвероят f(px) с увел массы мол уменшается
При одинак темп сред квадр скор мол кисл Меньше сред кв водор.
Распр
Ма-Бо: ![]()
потенциальная
эн частиц во внеш поле плюс сум кин
энергия мол
Распределение
электронов по состояниям
![]()
Размерность статистического веса: безразмерная величина
Распределение
электронов по энергиям
![]()
Распределение
Больцмана по состояниям
![]()
Распределение
Больцмана по состояниям

Распр
Боль f(E)= сист
частиц мал плот, у которых не прояв кван
св
сист
частиц мал плот, у которых не прояв кван
св
Распр
Макс по мод скор для Т1>Т2
показано на рис:
![]()
Распределение
фононов по состояниям имеет вид:

Реальные процессы в изол: в направ увел хаот движ частиц в системе
Распр Бозе-Эйн по эн –сред число бозонов в един малом интер эн
Система фононов описывается статистикой Бозе-Эйнштейна
Согласно
теореме о равнораспределении эн
![]() равно:
равно:
![]()
Среднее
значение
для
одноат ![]()
Среднее
значение  для
молекул
для
молекул ![]()
Среднее значение
![]() можно
найти
можно
найти ![]()
Статический вес системы: зависит от числа частиц системы
Средние скорости молекул T1=T2 , m1>m2: <v1> < <v2>
Случайная вел х принимает значения от 0 +∞. f(x)=Ce-bxb
Температура вырождения системы Tв. Для невыр Т>>Тв
Теплоём
электрон газа в металлах
![]() т.к.
средняя энергия
т.к.
средняя энергия
теплового
движения электронов в металле ![]()
Темп абсол черного тела Т=103 К. Вина В=6*1010 1/с*К. 6*1013 Гц
Термодинамическая сист наход в равновесном сост: E=const, S=Smax
Теплоемкость общей массы идеального одноат V=const: C=3R
Точка в фазовом пространстве для системы из N: микросостояние системы
Услов норм функ
Макс по мод скор: ![]()
У изолированной системы, находящейся в равн сост: Ω=Ωmin
Функция
распределения Ферми-Дирака по состояниям
![]()
Функ распр Фе-Дир по сост средн число фермионов в одном кв сост
Функция
распределения Ферми-Дирака по эн![]()
Функ
распр мол по проекции скор vx
,
пронорм на 1,:
Функция
распределения Фер-Дирака по эн при Т=0
![]()
Функция распр Макс по мод скор (плотность вероятности) f(υ) :
относительному числу молекул в единичном интервале скоростей
Функция распределения по энергии в квантовой статистике
среднее число частиц в единичном малом интервале энергии
Функция распределения частиц по энергиям в квантовой статистике
среднее число частиц в малом единичном интервале энергии
Функции распр мол идеального газа по проек скор
(плотность
вероятности) ![]() ,
m2>m1,
a T1=T2,:
,
m2>m1,
a T1=T2,:
![]()
Функция
распределения  .
Это означает
.
Это означает![]()
Функция
распределения Ферми-Дирака по мод имп
при Т=0
![]()
Функц
распр Бозе-Эйн наход путём усредн ![]() ,
K
,
K
набор квантовых чисел, задающ данное квантовое сост своб бозона
Функции распределения по проекции импульса рх (плотность вероятности)
для
разных газов, у которых m2>m1,
а T1=T2,
![]()
Формуле
планка ![]() имеет
смысл
имеет
смысл
Энергии фотонов, находящихся в единичном малом интервале частот
Формула
![]() представляет
собой зависимость хим
представляет
собой зависимость хим
потенциала от температуры для собственного полупроводника
Функ
распр Фе-Дир по сост може:
![]() ,
где
,
где ![]()
вероятность
нахождения ![]() фермионов
в k -том квантовом сост
фермионов
в k -том квантовом сост
Функ
распр Фе-Дир по сост нахо ![]() ,
k
,
k
Набор квантовых чисел, задающих квантовое сост частицы в атоме
Функция
распр частиц по энергиям в квантовой
стат ![]()
Функ
распр молекул идеал f(v)(плотность
вероятности):
![]()
Формула
для концен электр в зоне провод п/п
n-типа ![]()
функция
распр Фер-Дир по мод квазиимп

Химический
потенциал фононов ![]() 0
0
Химический
потенциал системы бозонов ![]() :
:
![]()
Хим потен собствен п/п Т=0 наход в середине запрещенной зоны
Число возмож сост сист N =100 кван частиц :
Число
доступных сост в элементе фазо прост
![]() →
∞
→
∞
Число доступных микросостояний в некотором фазовом объеме ΔГ:
бесконечно для классической частицы, т.к. в каждый момент времени
объем, который в фаз простр опред ее состояние, стремится к нулю
Ширина
разреш энерг зоны ![]() N=1022
2*10-22
эВ
N=1022
2*10-22
эВ
Энергетич спектр электронов в кристаллах состоит из разрешённых
и запрещённых зон одинаковой ширины
Энергия
квантового гармонического осциллятора
![]()
Энергия Ферми… максимальная энергия фермионов при Т=0
Энтропия неизолированной системы при необрат теплообмене:
может как и увеличиваться, так и уменьшаться в завис от условий
Электроны, находящиеся в верхних разрешённых электрических
хаотически по всему кристаллу в периодичном поле всех ядер