
2. Классическая статистика
2.1 Общее представление и элементы теории
НТ1(З). Каноническое
распределение Гиббса имеет вид![]() ,
где постоянная
,
где постоянная
С
равна :
![]()
А)
![]() ;
;![]()
В)
![]() ;
;
*С)
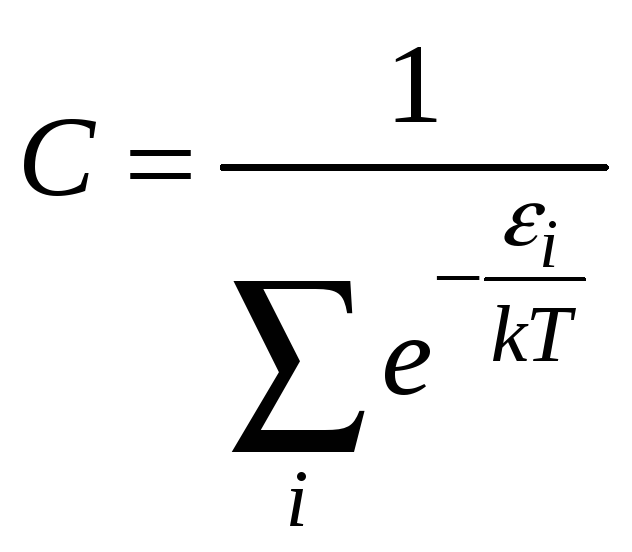 ;
;
D)
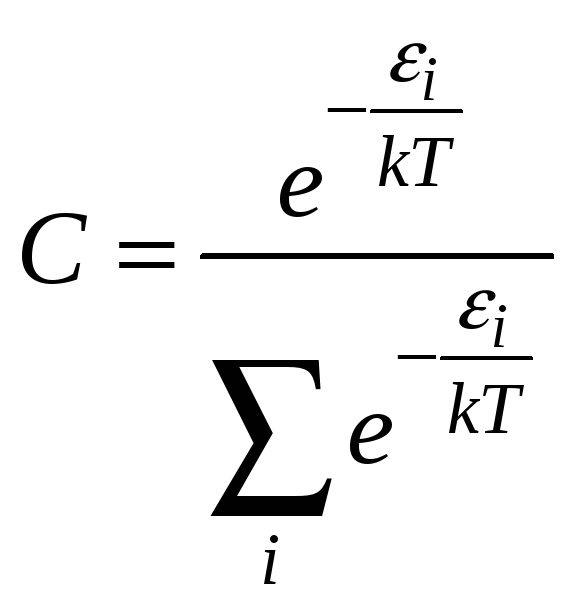 .
.
НТ1(З). Выражение
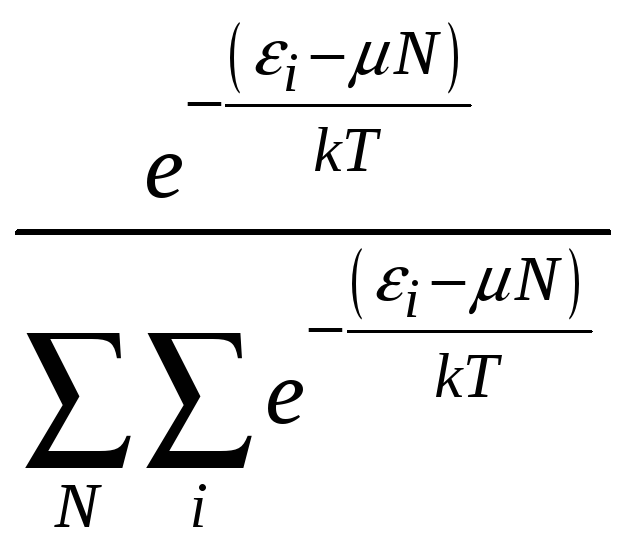 :
:
А) имеет смысл распределения частиц по энергиям;
В) равно среднему числу частиц в состоянии с энергией εi;
*С) равно вероятности встретить подсистему, состоящую из N частиц,
в состоянии с энергией εi;
D) равно нормировочному множителю в большом каноническом
распределении Гиббса.
НТ1(З).
![]() можно
найти, вычислив значение интеграла
можно
найти, вычислив значение интеграла
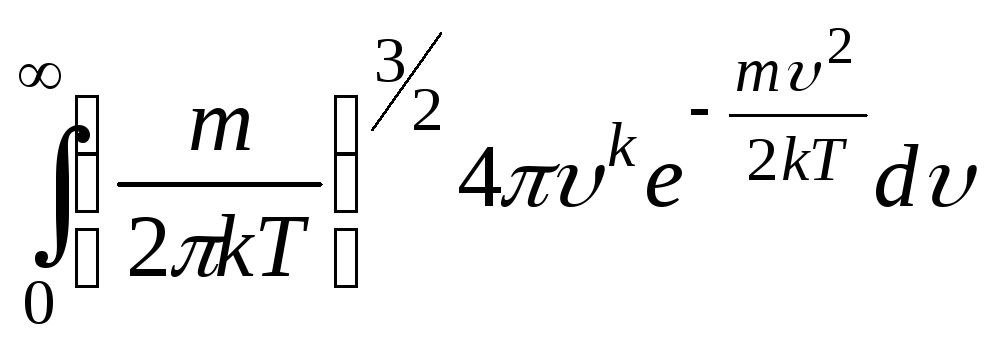 ,
где k=….
(*Ответ: 4)
,
где k=….
(*Ответ: 4)
НТ1(З). Если F(x) – плотность вероятности или функция распределения
случайной
величины
х,
то выражение
![]()
(*Ответ:<f(x)>)
НТ1(О). Интеграл
 ,
где k=….
(*Ответ: 1)
,
где k=….
(*Ответ: 1)
НТ1(З). Если F(x) – плотность вероятности или функция распределения
случайной
величины
х,
то выражение

*A)
![]() ;
;
*B)
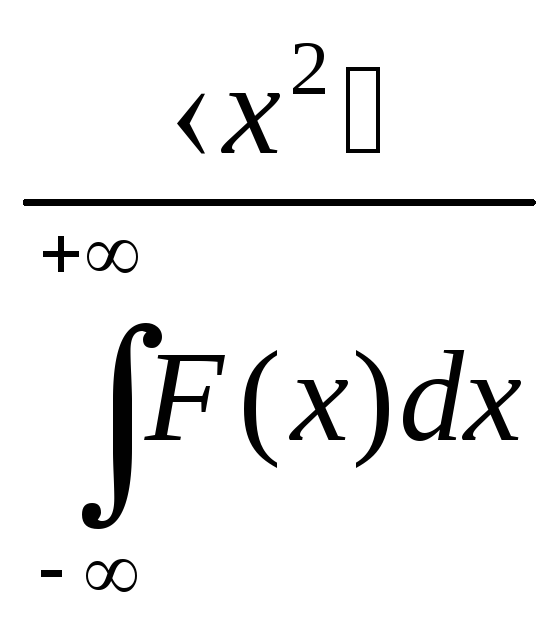 ;
;
C)
![]() ;
;
*D)![]() ;
;
E)
![]()
Правильные выражения:
НТ2(С). Найдите все возможные соответствия между левым и правым
столбиками. Ответ дайте в виде: k-l, m-n, …
-
а) значение интеграла равное 1;
b) среднее значение
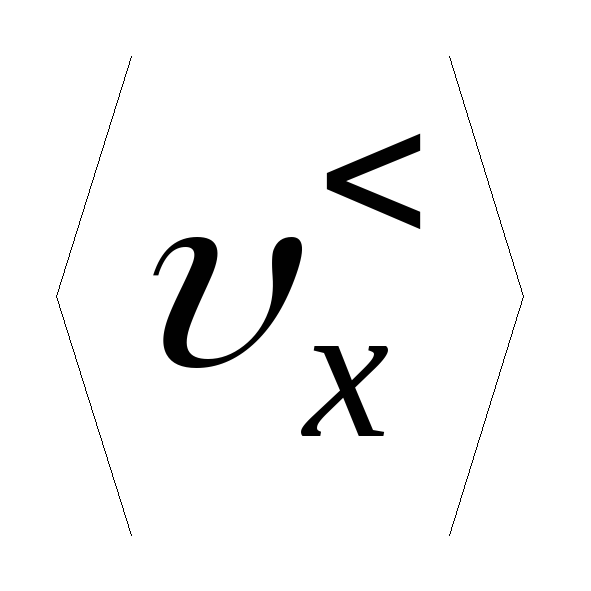 ;
;c) среднее значение
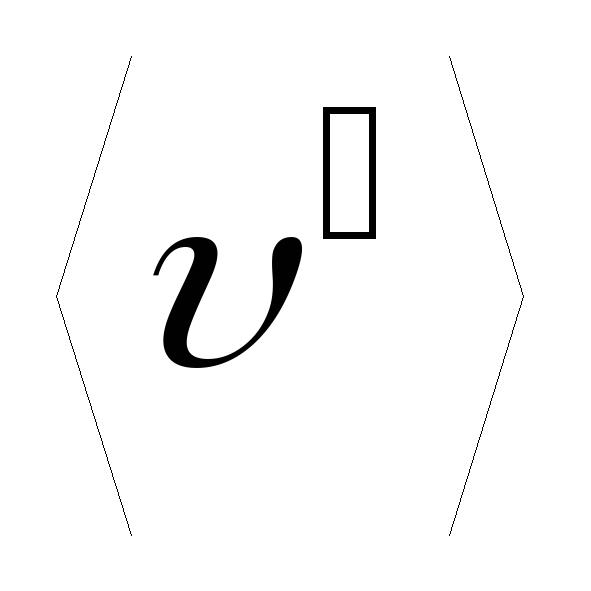 .
.а)
 ;
;b)
 ;
;c)
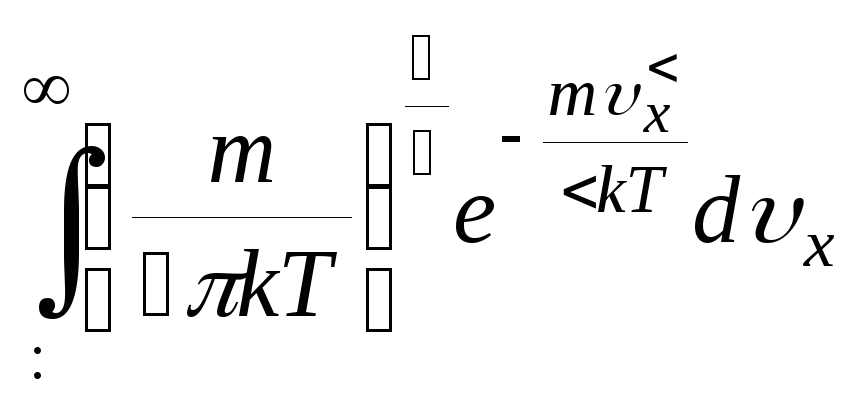 ;
;d)
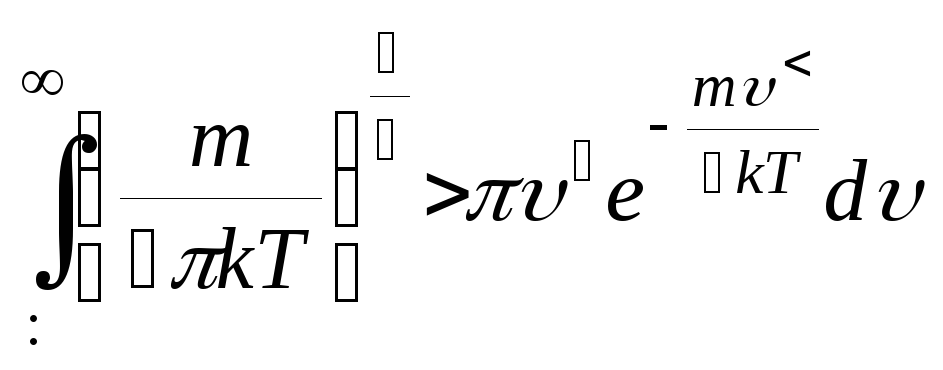 .
.
(*Ответ:a-d, c-a)
НТ1(З).Средние
скорости молекул идеальных газов, у
которых
![]() ,
а
,
а
массы
молекул
![]() >
>
![]() :
:
*А)
![]() <
<![]() ;
;
В)
![]() >
>![]() ;
;
C)
![]() =
=![]() ;
;
D)
![]() не
связана с их массой.
не
связана с их массой.
НТ1(З). Если число
молекул идеального газа выросло в четыре
раза (N2=4N1),
а
![]() и
и
![]() ,
то относительное число молекул, имеющих
скорости от
,
то относительное число молекул, имеющих
скорости от
![]() до
до
![]() :
:![]()
А) увеличилось в 4 раза;
В) уменьшилось в 4 раза;
*С) осталось прежним;
D) увеличилось в 2 раза.
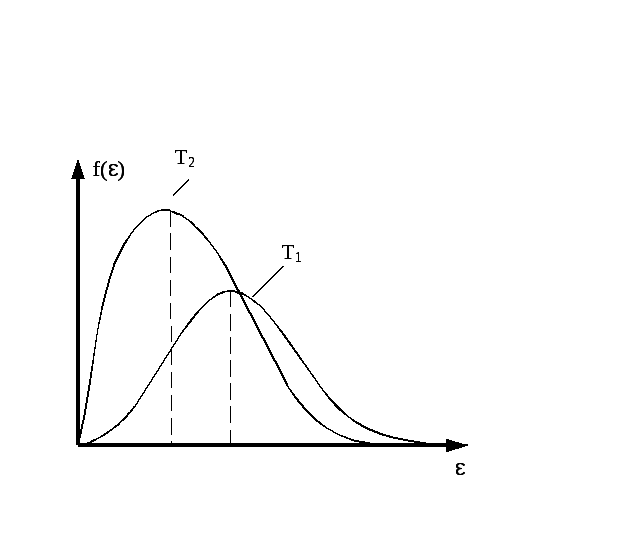
НТ1(З). F(x) – плотность вероятности или функция распределения случайной величины х.
Среднее значение
![]() равно:
равно:
А)![]() ;
;
В)
![]() ;
;
С)
![]() ;
;
*D)
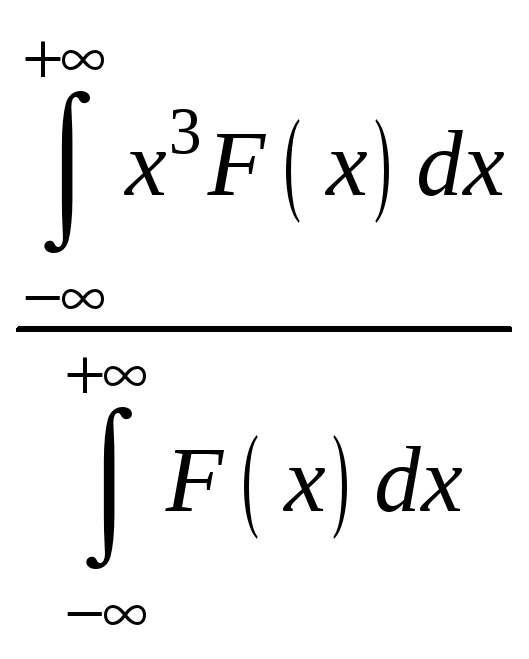 .
.
НТ1(З). f(p)-
функция распределения по модулю импульса
для молекул идеального газа. Среднее
значение
![]() равно:
равно:
А)
![]() ;
;
*В)
![]() ;
;
С)
![]() ;
;
D)
![]()
НТ1(З). Молекулы идеального газа :
А) всегда имеют целый спин;
В) всегда имеют полу целый спин;
*С) могут иметь как целый, так и полу целый спин;
D) вообще не имеют спина.
НТ1(О). При одинаковых температурах наиболее вероятная скорость
молекул кислорода ……… наиболее вероятной скорости молекул водорода. Вставьте
слово.
(* меньше)
НТ1(О). При одинаковых температурах средняя квадратичная скорость молекул кислорода ………средней квадратичной скорости молекул водорода. Вставьте слово.
(* меньше)
НТ1(О). При одинаковых температурах средняя энергия молекул кислорода……… средней
энергии молекул водорода. Вставьте слово.
(*равна)
НТ1(З). Наиболее вероятное значение энергии для молекул идеального газа:
А) ~![]() ;
;
В) ~![]() ;
;
C) ~m;
*D)
не зависит от m![]() .
.
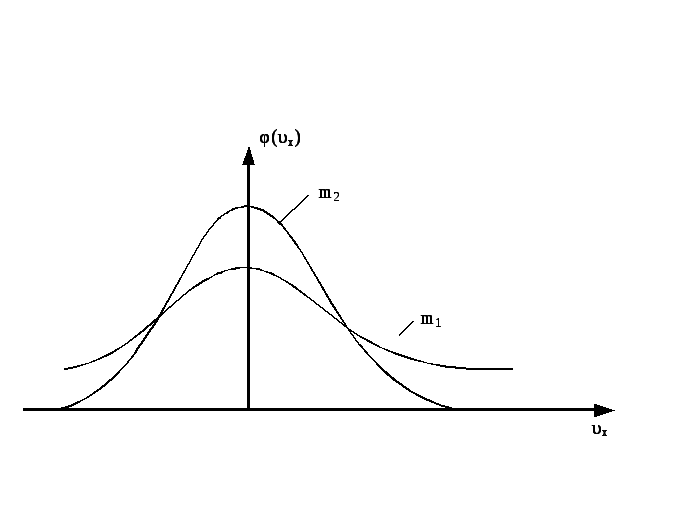
НТ2(О). При Т=const
максимальное значение плотности
вероятности
![]() с
увеличением массы молекул ……. Вставьте
слово.
с
увеличением массы молекул ……. Вставьте
слово.
(*уменьшается)
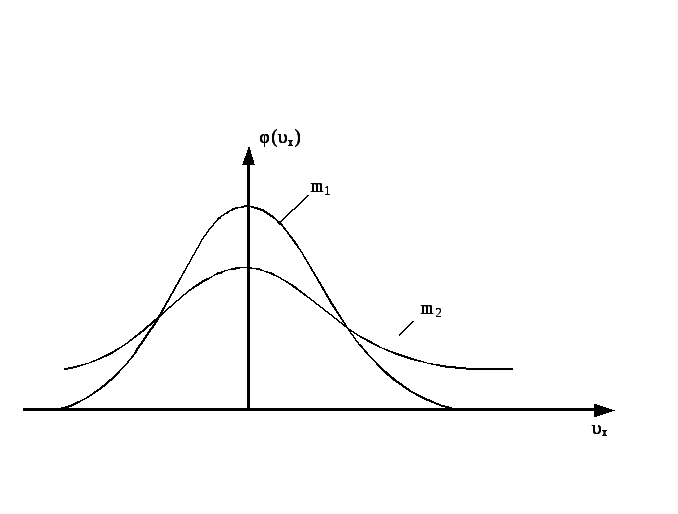
НТ1(З). В функции распределения Максвелла по проекции скорости
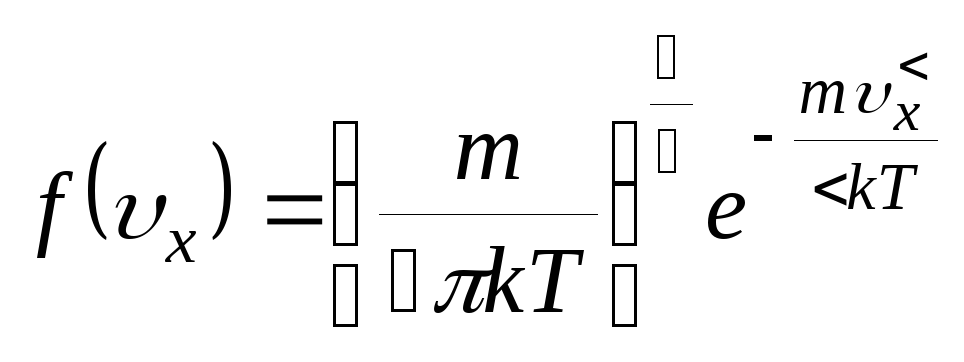 m
– это:
m
– это:
*А) масса одной молекулы определенного газа;
В) общая масса газа;
С) масса одного моля;
D) некоторая масса частицы, одинаковая для всех газов.
НТ1(З). Плотность
вероятности или функция распределения
молекул идеального газа по проекции
скорости имеет вид
![]() ,
где нормированный множитель C
равен:
,
где нормированный множитель C
равен:
А)
![]()
![]() ;
;
B)
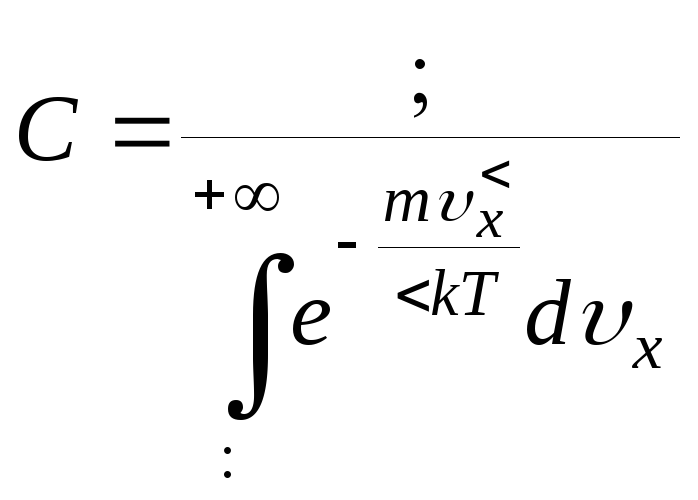 ;
;
*C)
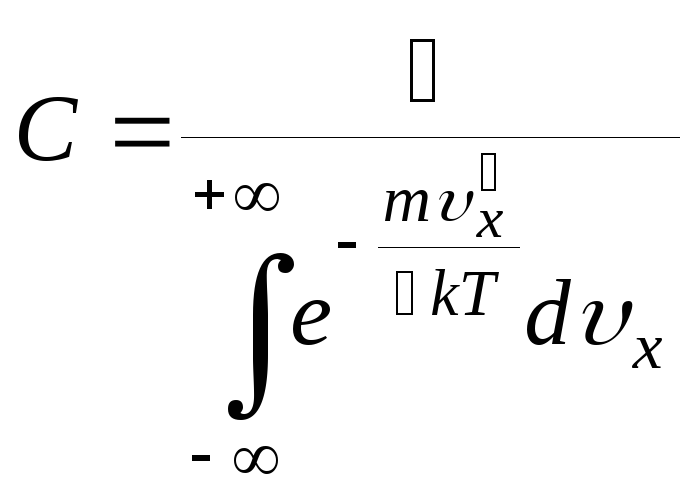 ;
;
D)
![]() .
.
НТ1(З). Значения
интегралов
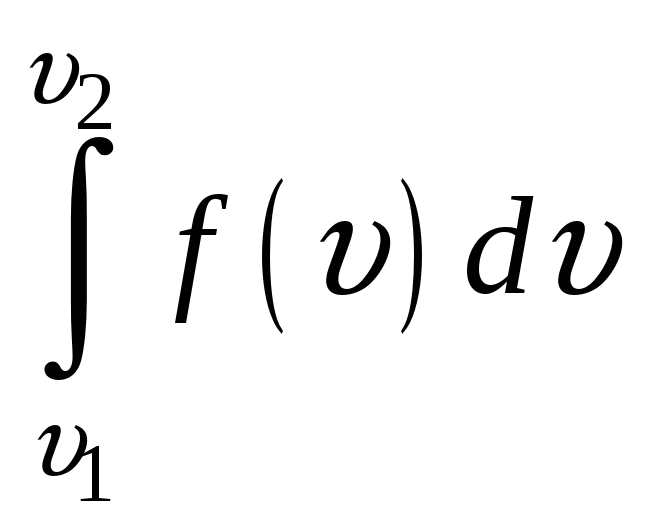 для
разных газов
для
разных газов![]() при
при
одинаковых температурах:
А) всегда совпадают;
В) тем больше, чем больше масса одной молекулы;
С) тем больше, чем меньше масса одной молекулы;
*D) нельзя сравнить, так как значения интеграла зависят от выбранного
интервала скоростей.
-
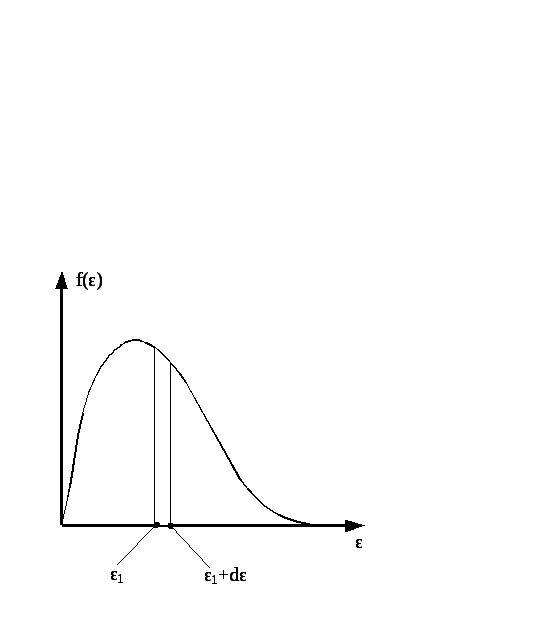
НТ1(З).
 -
плотность
-
плотность
вероятности или функция распределения молекул идеального газа по энергии. Заштрихованная площадь равна:
А) общей энергии всех молекул
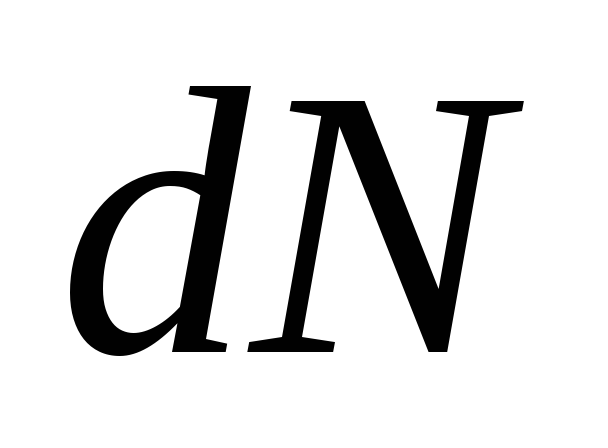
с энергиями от
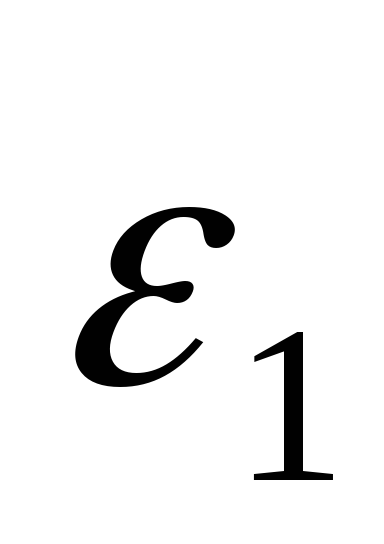 до
до
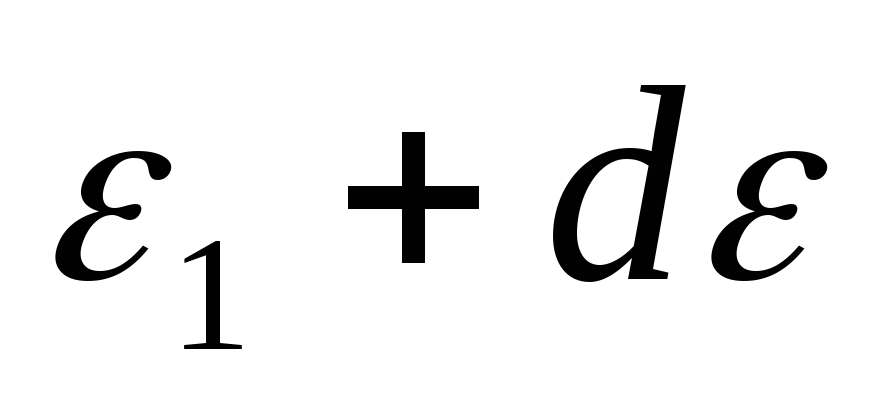 ;
;В) числу молекул
 ,
имеющих
,
имеющих
энергию от
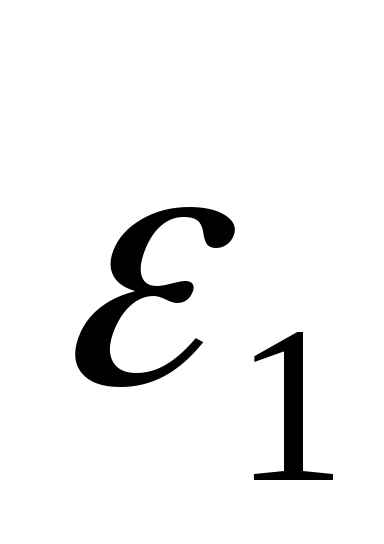 до
до
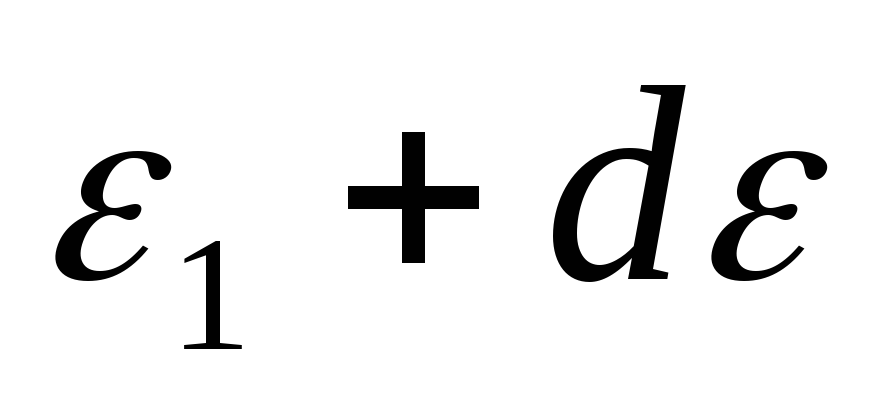 ;
;С) вероятности встретить частицы с
энергией
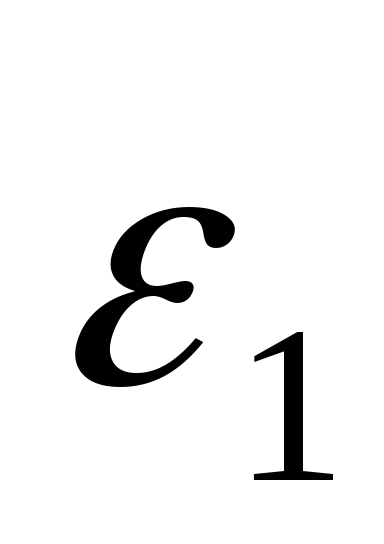 ;
;*D) относительному числу молекул
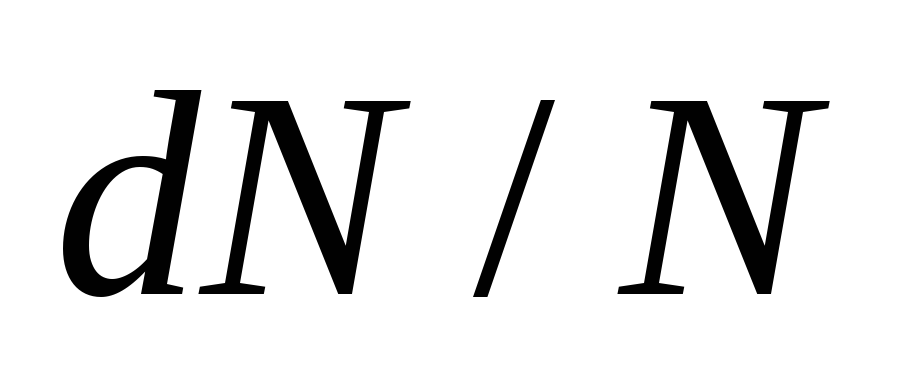 ,
имеющих энергию от
,
имеющих энергию от
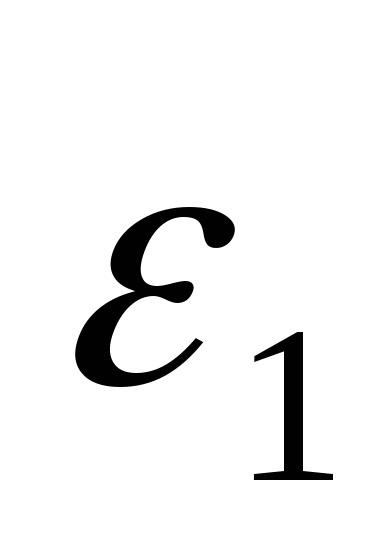 до
до
 ;
;
|
НТ2(З).
Среднее значение
пользуясь любым выражением, кроме …
*А)
В)
С)
D)
|
|
НТ1(З).
Функция распределения молекул
идеального газа по модулю скорости
А)
*В)
С)
D) безразмерная
|
|
НТ1(З).
Правильным соотношением для функции
распределения молекул идеального
газа по проекции импульса
*А)
В)
С)
D)
|
|
НТ1(З). На рисунке показано распределение Максвелла по модулю скорости для некоторого газа при разных температурах. При этом площади под кривыми (Si) и температуры (Тi) удовлетворяют соотношению:
*А) S1=S2=S3=1, T3>T2>T1; B) S1=S2=S3=1, T1>T2>T3; C) S1>S2>S3, T1>T2>T3; D) S1<S2<S3, T1<T2<T3 |
|
НТ1(З).
А)
*В)
C)
D)
НТ2(З).
Если
A)
B)
C)
*D)
|
|
НТ1(З).
Среднее значение
А)
В)
С)
*D)
НТ1(З).
А) 1;
В)
С)
*D)
НТ1(З).
Если
А)
*В) 0
С)
D)
НТ1(З).
Распределение Максвелла-Больцмана
для идеального газа имеет вид:
А) потенциальная энергия взаимодействия молекул друг с другом плюс суммарная кинетическая энергия частиц; *В) потенциальная энергия частиц во внешнем поле плюс суммарная кинетическая энергия молекул; С) только кинетическая энергия молекул; D) только потенциальная энергия частиц во внешнем поле. НТ1(З).
Для функций распределения
А)
*В)
С)
D)
НТ2(З).
А)
В)
*С)
D)
НТ2(З).
Если функция распределения по энергии
для молекул идеального газа пронормирована
на число частиц (
А) среднему
значению
В) вероятности
встретить частицы с энергиями от
С) числу частиц,
имеющих энергию
*D)
суммарной энергии всех частиц, у
которых
НТ1(З).
Наиболее вероятное значение проекции
скорости
А)
B)
*C) 0;
D)
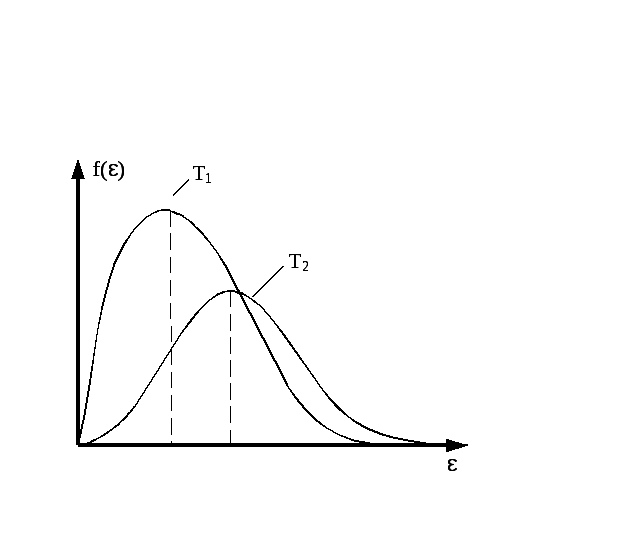
НТ1(З). Распределение Максвелла по модулю скорости для некоторого идеального газа при Т1>Т2 показано на рисунке:
А)
*В)
С)
|
|
D)
НТ1(З).
Если
А)
B)
C)
*D) НТ1.
Функции распределения молекул
идеального газа по проекции скорости
(плотность вероятности)
А)
*В)
С)
D)
НТ1(З).
Если
*A)
B)
C)
D)
НТ1(З).
А) от -∞ до ∞;
В)
*С)
D)
НТ2(З).
А)
B)
C)
*D)
НТ1(З).
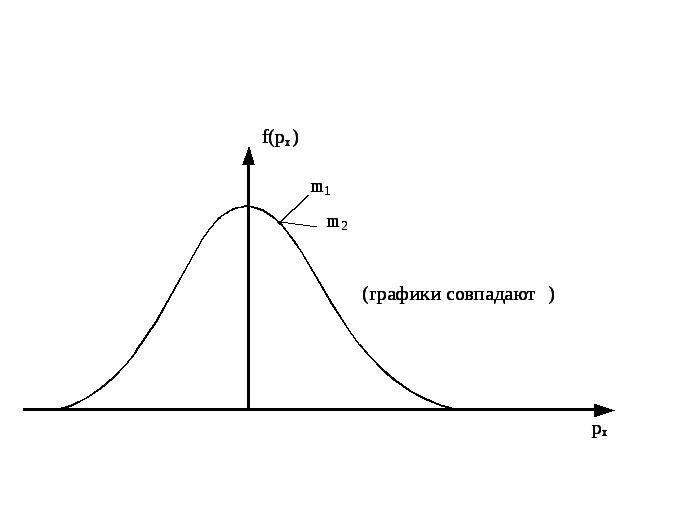
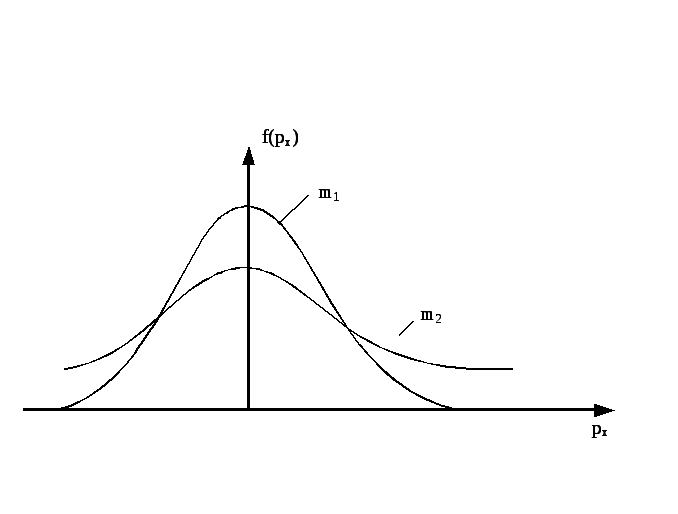
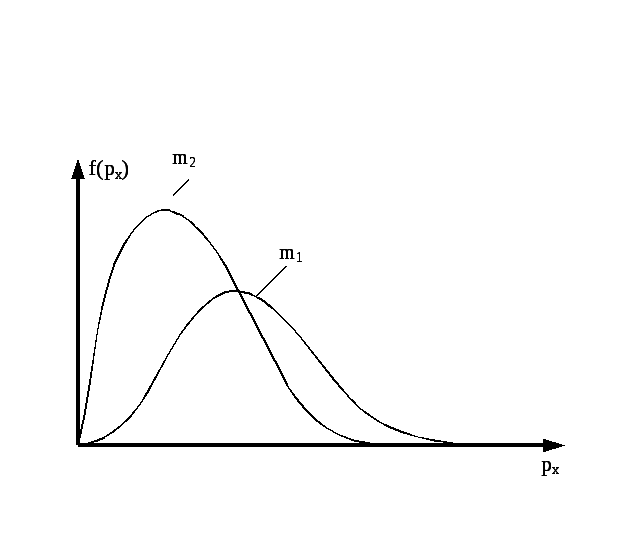
Функции распределения по проекции
импульса рх
(плотность вероятности) для разных
газов, у которых m2>m1,
а
А)
*В)
С)
D)
НТ1(З).
F(x)
– плотность
вероятности или функция распределения
случайной величины
х. Среднее
значение
А)
*B)
C)
D)
НТ1(З).
Согласно теореме о равнораспределении
энергии по степеням свободы
А)
*B)
C)
D)
НТ1(З).
*А)
B)
C)
D)
НТ1(З).
Функции распределения по энергии
А)
В)
*С)
D)
НТ1(З). Если х - случайная физическая величина, принимающая ряд дискретных значений
х1,
х2,
…хп,
а Рi
– вероятность появления xi,
то среднее значение
*А)
B)
C)
D)
НТ1(З).
Выражение
А) 1;
В) среднему
значению
С) среднему
значению
*D) 0.
НТ1(З). Условием нормировки функции распределения Максвелла по модулю скорости для молекул идеального газа является выражение:
А)
В)
*С)
D)
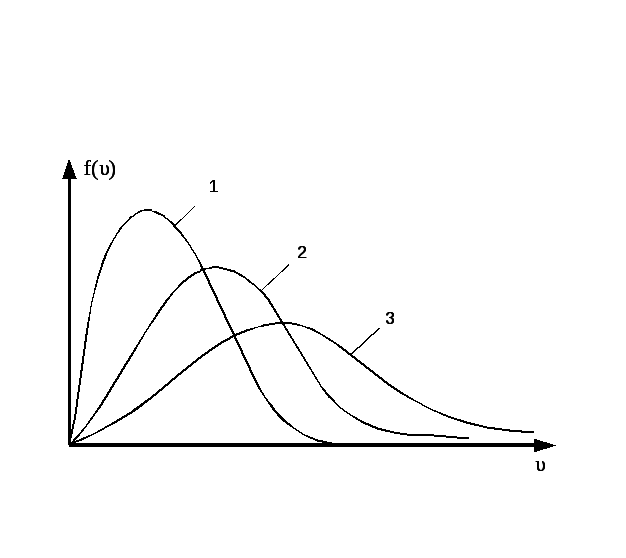
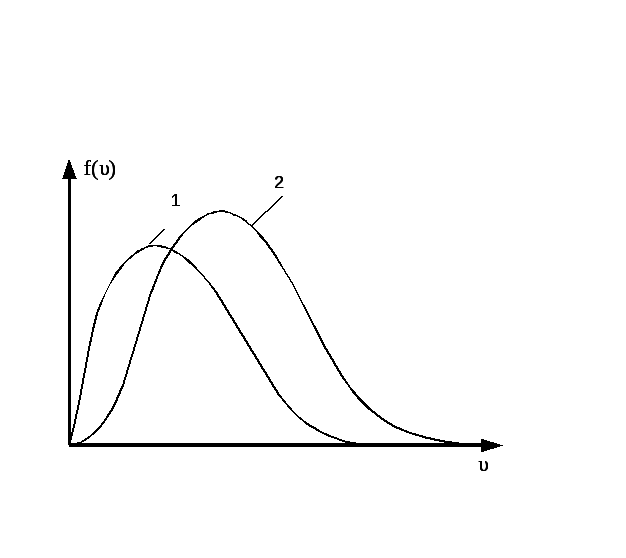
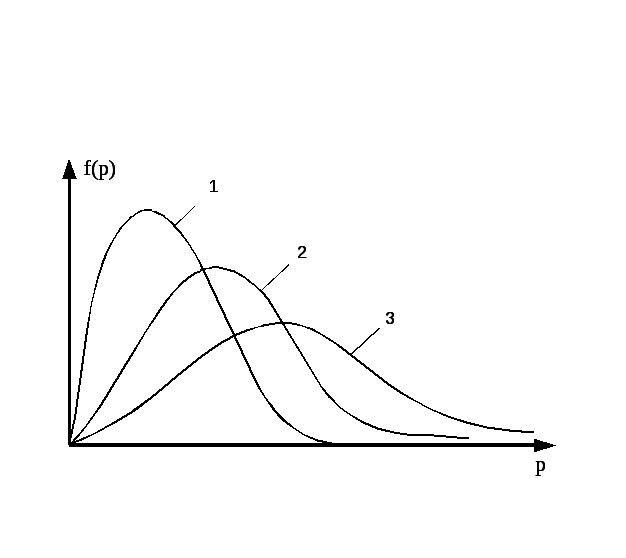
НТ1(З). Графики 1,2,3 соответствуют трем функциям распределения Максвелла по модулю импульса для одного и того же газа в сосуде V при разных T. Наименьшей энтропии соответствует график ….. (*Ответ: 1)
НТ1(З).
Среднее значение
А)
В)
*С)
D)
НT1(З).
А) средняя скорость, где m – масса одной молекулы; В) средняя скорость, где m – молярная масса газа; С) средняя квадратичная скорость, где m – общая масса газа. *D) средняя квадратичная скорость, где m – масса одной молекулы.
НТ2(З). Перейти от классической функции распределения по модулю импульса
A) можно, заменив p на mu в выражении f(p); *B) можно, заменив p на mu и dp на mdu в выражении f(p)dp; C) можно, выполнив любое из преобразований (А) или (В), так как получится одно и тоже выражение; D) нельзя ни одним из преобразований
НT1(З).
Функция распределения молекул
идеального газа по проекции скорости
пронормированная на 1, имеет вид:
А)
*В)
С)
D)
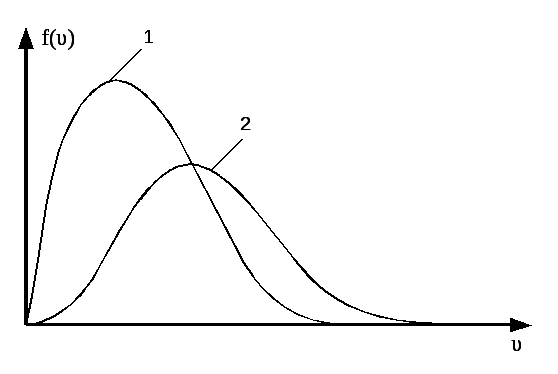
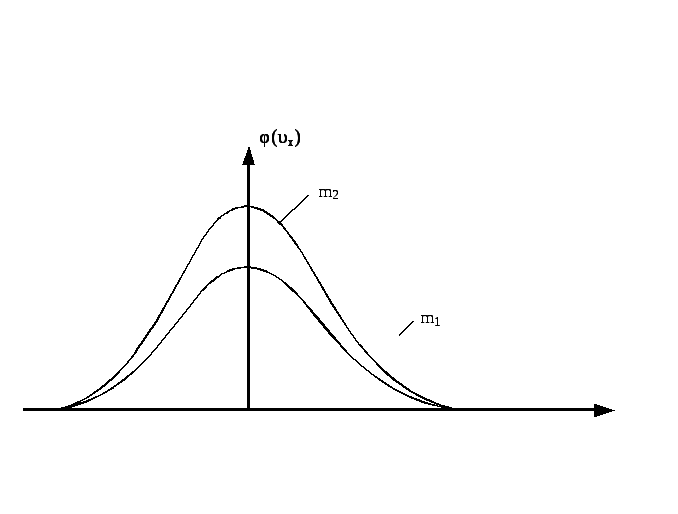
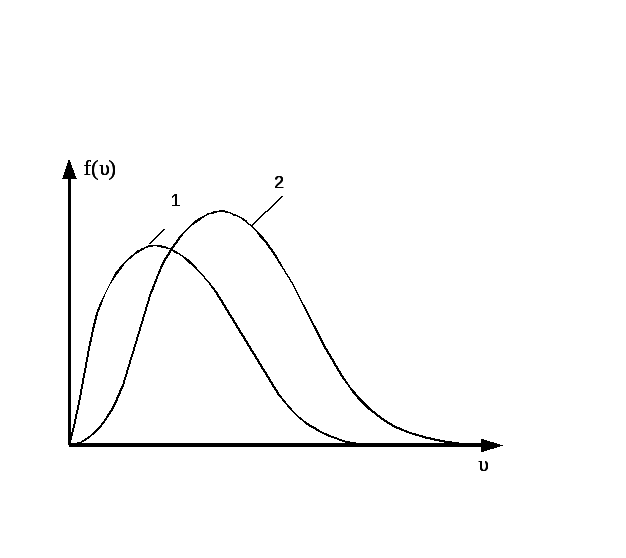
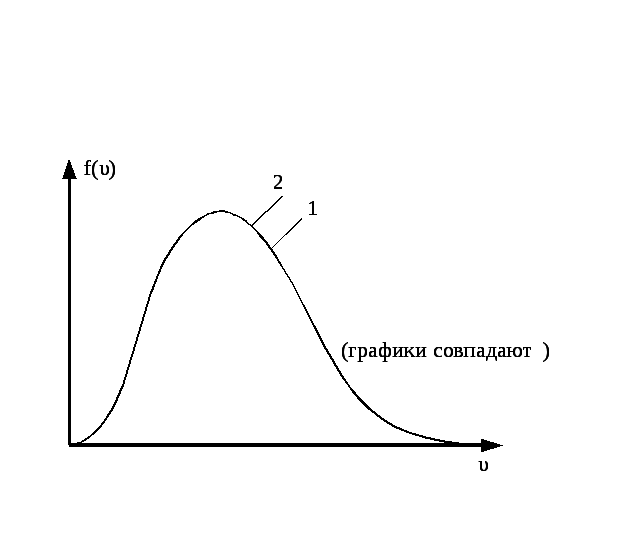
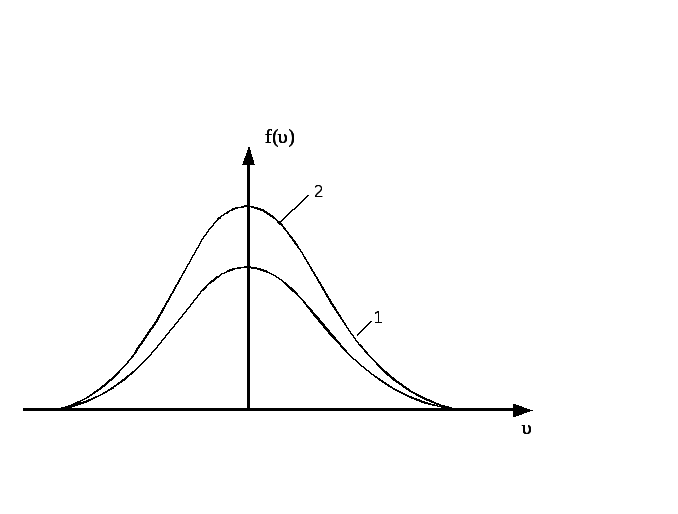
НT2(З).
Правильным рисунком функций плотности
вероятности f(v)
для одинаковых газов, у которых
А)
В)
*С)
D)
НТ1(З).
Если F(x)
– функция распределения случайной
величины
х, а f(x2)
– некоторая функция этой величины,
то
A) B)
*C)
D) E)
НT1(З).
Для
*А)
В)
С)
D)
НТ2(З). Функция распределения Максвелла по модулю скорости (плотность вероятности) f(υ) равна:
А) числу молекул с данной скоростью; В) вероятности того, что скорость молекулы равна υ; *С) *C) относительному числу молекул в единичном интервале скоростей; D) относительному числу молекул в интервале скоростей dυ
НТ1(З).
f(x2)
– некоторая функция случайной величины
x.
Интеграл
A)
B)
*C)
D)
E)
Задачи
НT1(О).
Если число молекул идеального газа
увеличилось
то отношение
вероятностей встретить молекулы с
энергиями от (*Ответ: 1) НТ1(О).
Если отношение наиболее вероятных
значений скоростей
НТ2(С). Приведите в соответствие условия из левого столбика и отношение
максимальных
значений функций распределения
k-l, m-n,…
а)
b)
с)
d)
(*Ответ:a-b, b-c, c-a, d-b)
НТ1(О). Для функции распределения Максвелла по проекции импульса
HТ1(О). Для функций распределения Максвелла по проекциям импульсов
НТ1(О). НТ1(О).
Вероятность встретить молекулы
идеального газа, у которых проекции
скорости
НТ1(О).
Отношение наиболее вероятных значений
энергий
НТ1(О).
Отношение средних значений
НТ1(О).
Если температура 2-х идеальных газов
Т2=2Т1,
а массы молекул m2=2m1,
то отношение значений средних энергий
НТ1(О).
При увеличении температуры идеального
газа Т2=4Т1
отношение максимальных значений
функций распределения по проекции
скорости
НТ2(О). Отношение интегралов для молекулы водорода Н2 (молярная масса водорода 210-3кг/моль) при Т=300 К с учетом
NA»6×10231/моль
НТ1(О).
Средняя кинетическая энергия одного
атома идеального газа равна 6,9·10-21
Дж. Среднее значение
НТ1(О).
Отношение максимальных значений
функций распределения для молекул
идеального газа
НТ1(З).
Для молекул идеального газа значения
интегралов
A) I1= I2; *B) I1<I2; C) I1>I2; D) нельзя сравнить, не зная температуры.
НТ1(З). Для классической функции распределения по модулю скорости при условии
Т=const,
а u2>u1
отношение
A) всегда >1; B) всегда <1; C) >1, если u1 и u2 больше uнв - наиболее вероятной скорости; *D) >1, если u1 и u2 меньше uнв; *E) <1, если u2 и u1 больше uнв ; F) <1, если u1 и u2 меньше uнв ; G) >1, если u1<uнв<u2 . Правильные утверждения:
НТ2(З). Перейти от классической функции распределения по модулю скорости
A)
можно, заменив
B)
можно, заменив
*C)
можно, заменив
D) можно, выполнив любое из преобразований (А) или (В), так как получится одно и тоже выражение; E) нельзя ни одним из этих преобразований.
НТ1(О). Для данного газа в равновесном состоянии отношение средней энергии частиц к наиболее вероятной энергии при заданной температуре равно… (*Ответ:3)
НТ1(З).
Если f(ux)
– функция распределения молекул
идеального газа по проекции скорости,
то для интегралов:
A)
B)
C)
*D)
E)
F)
НТ1(З). При T=const максимальное значение функции распределения по проекции импульса f(px): A)~
B)~
C)~
*D)~ E) не зависит от m.
НТ1(О).
Значения функций распределения по
проекции скорости при
(*Ответ: 9)
НТ2(О).
Значения функций распределения по
проекции скорости при
распределения
НТ1(О).
Наиболее вероятное значение проекции
скорости
Т=400 К равно …. (*Ответ: 0)
НТ2(О).
Для молекулы азота N2
(молярная масса азота 28 г/моль) наиболее
вероятное значение модуля скорости
(*Ответ: 420)
НТ2(О). Для молекулы кислорода О2 (молярная масса кислорода 32 г/моль) значение средней квадратичной скорости при Т=400 К равна ….. м/c. R=8,31 Дж/К×моль. Ответ округлите до десятков. (*Ответ: 560).
НТ2(З).
Случайная величина х
принимает значения от 0 +¥.
Функция распределения случайной
величины х
или плотность вероятности имеет вид
*A) b;
B)
C)
D)
E)
F)
|
3. Квантовая статистика. (72 задания).
1.НТ1(3). Основной постулат квантовой статистики - это ...
*А) принцип тождественности частиц;
В) принцип соответствия;
С) принцип дополнительности;
D) принцип относительности.
2.НТ1(3). Основной постулат квантовой статистики (принцип тождественности) является следствием того, что ...
*А) описание движения отдельной частицы носит вероятностный характер;
В) в статистической физике изучаются системы, состоящие из большого количества частиц;
С) частицы находятся в постоянном хаотическом движении;
D) частицы принадлежат классу фермионов или бозонов.
3.НТ1(3). Функция распределения по энергии в квантовой статистике – это
А) вероятность
нахождения частицы с энергией
![]() ;
;
В) плотность
вероятности нахождения частицы в
интервале
![]() ,
,![]() ;
;
*С) среднее число частиц в единичном малом интервале энергии;
D)
среднее число частиц с энергией
![]() .
.
![]()
4.НТ1(С). Для каждого типа частиц выберите их свойства:
А) Фермионы А) симметричная волновая функция;
В) Бозоны В) антисимметричная волновая функция;
С) целый спин;
D) полуцелый спин;
E) подчиняются принципу Паули;
F) не подчиняются принципу Паули.
Ответ: AB, AD, AE, BA, BC, BF
5.НТ1(3). Принцип Паули утверждает, что ...
А) в одном квантовом состоянии может находиться 0 или 1 частица;
*В) в одном квантовом состоянии может находиться не более одного фермиона;
С) на одном энергетическом уровне может находиться не более одного фермиона;
D) в одном квантовом состоянии может находиться любое число фермионов.
6.НТ1(3). Одному квантовому состоянию (без учёта спина) соответствует фазовый объём …
А)![]() =
2
=
2![]() ;
*В)
;
*В)
![]() =
=![]() ; С)
; С)
![]() =
=![]() ; D)
; D)
![]() =
=![]() .
.
7.НТ1(О). Запишите
формулу для количества квантовых
состояний d
![]() в фазовом объеме dГ,
используя шаблон
в фазовом объеме dГ,
используя шаблон
![]() =
=
![]()
a {![]() ;
;
![]() ;
;
![]() };
};
b {![]()
![]() ;
;
![]() };
};
@ ={+;
-; /}.
={+;
-; /}.
Ответ: a1b1/a3
8.НТ1(3). Одному квантовому состоянию для N частиц (без учёта спина) соответствует фазовый объём …
*A)
![]() ;
B)
N
;
B)
N![]() ;
C)
3
;
C)
3![]() ;
D)
3Nh.
;
D)
3Nh.
9.НТ1(3). Одному квантовому состоянию для одной частицы в трехмерном пространстве соответствует фазовый объем
A)
![]() ;
B)
;
B)
![]() ;
*C)
;
*C)
![]() ;
D)
;
D)
![]() .
.
10.НТ1(С). Для каждого вида статистики выберите свойства частиц и волновых функций
|
А) Ферми-Дирака |
А) Антисимметричная волновая функция; |
|
В) Бозе-Эйнштейна |
В) Симметричная волновая функция; |
|
С) Максвелла-Больцмана |
С) Частицы с целым спином; |
|
|
D) Частицы с полуцелым спином; |
|
|
Е) Количество квантовых состояний конечно; |
|
|
G) Частицы подчиняются принципу Паули; |
|
|
H) Квантовое взаимодействие частиц не проявляется. |
Ответ: AA, AD, AG, BB, BC, CH
11.НТ1(3). Функция распределения Ферми-Дирака по состояниям – это …
*А) среднее число фермионов в одном квантовом состоянии;
В) вероятность
нахождения фермиона на уровне с энергией
![]() ;
;
С) среднее число
фермионов с энергией
![]() ;
;
D)
плотность вероятности нахождения
фермиона в интервале
![]() ,
,![]() .
.
12.НТ1(3). Функция распределения Ферми-Дирака по состояниям имеет вид …
*А) ;
В)
;
В)![]() ;
С)
;
С)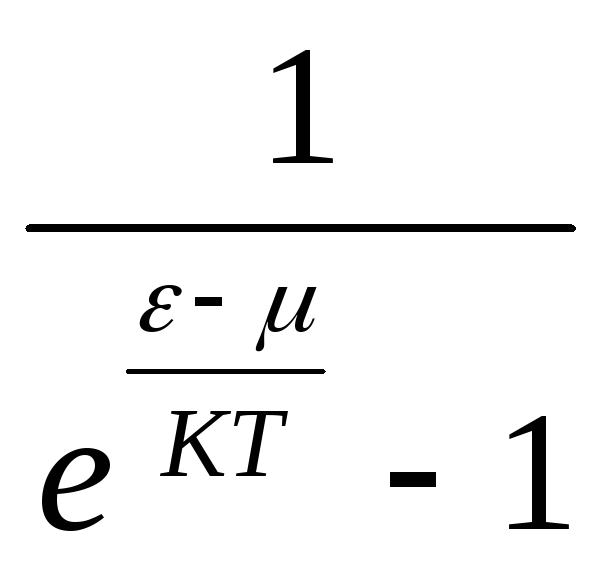 ;
D)
;
D) .
.
13.НТ1(3). Функция распределения Ферми-Дирака по состояниям может быть получена, исходя из формулы:
*А)
![]() ,
где
,
где
![]() вероятность нахождения
вероятность нахождения
![]() фермионов в k
-том квантовом состоянии;
фермионов в k
-том квантовом состоянии;
В)
![]() ,
где
,
где
![]() то же что и в пункте А;
то же что и в пункте А;
С)
![]() ,
где
,
где
![]() -
вероятность нахождения фермиона на
K-том
энергетическом уровне;
-
вероятность нахождения фермиона на
K-том
энергетическом уровне;
D)
![]() ,
где
,
где
![]() -
то же самое что и в пункте С.
-
то же самое что и в пункте С.
14.НТ1(3). Функция
распределения Ферми-Дирака по состояниям
находится по формуле
![]() ,
где k
– это ...
,
где k
– это ...
А) Номер энергетического уровня;
*В) Набор квантовых чисел, задающих квантовое состояние частицы в атоме;
С) Набор квантовых чисел, задающих квантовое состояние свободной частицы;
D) Постоянная Больцмана.
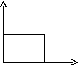
15.НТ1(3). На рисунке приведено распределение
f
1
ε
0
А) Ферми-Дирака по энергиям при любой температуре;
*B)
Ферми-Дирака по состояниям при
![]() ;
;
C)
Больцмана
![]() ;
;
D)
Максвелла-Больцмана при отсутствии
внешних сил и
![]() .
.
16.НТ1(3). На рисунке приведены распределения

A) Ферми-Дирака по состояниям, кривая 1 соответствует Т>0, кривая 2 – Т=0;
*B) Ферми-Дирака по состояниям, кривая 1 соответствует Т=0, кривая 2 – Т>0;
C) Ферми-Дирака по энергиям, кривая 1 соответствует Т>0, кривая 2 – Т=0;
D) Ферми-Дирака по энергиям, кривая 1 соответствует Т=0, кривая 2 – Т>0.
17.НТ1(3). На рисунке
приведено распределение Ферми-Дирака.
Интервал энергий
![]() примерно равен…
примерно равен…
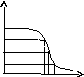
<n![]() >
>
1
0,75 А) T/2; B) KT;
0,5 *С) 2KT; D) 3KT.
0,25
ε![]() μ
ε
μ
ε![]()
![]() ε
ε
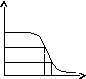
18.НТ1(3). На рисунке приведено распределение Ферми-Дирака.
f
0
ε![]() ε
ε![]() ε
ε
Каждое состояние
с энергией в интервале
![]() заполнено
заполнено
А) Полностью; *B) Частично;
С) Наполовину; D) Не заполнены.
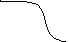
19.НТ1(3). На рисунке приведено распределение Ферми-Дирака.
f
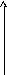
 1
1
0 ε
ε![]() ε
ε
Состояния с
энергиями в интервале
![]() заполнены ...
заполнены ...
A) полностью, в каждом находится два фермиона;
*B) полностью, в каждом находится один фермион;
C) частично;
D) не заполнены.
20.НТ1(3). Функция
распределения
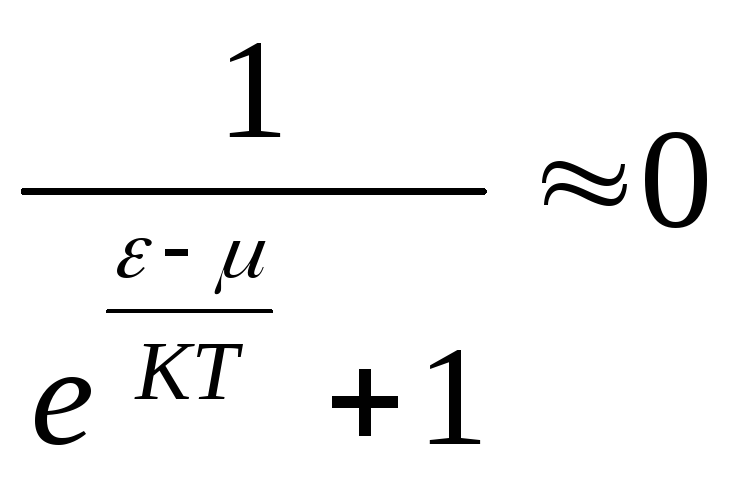 .
Это означает, что ...
.
Это означает, что ...
*А)
![]() ;
В)
;
В)![]() ;
С)
;
С)![]() ;
D)
;
D)![]() .
.
21.НТ1(О). Среднее
количество электронов в металле при
T>0
в одном состоянии с энергией
![]() равно ... Ответ записать в виде десятичной
дроби (округлить до десятых).
равно ... Ответ записать в виде десятичной
дроби (округлить до десятых).
Ответ: 0,3
22.НТ1(О). Среднее
количество электронов в металле в одном
квантовом состоянии с энергией
![]() при Т>0 равно… Ответ записать в виде
десятичной дроби (округлить до десятых).
при Т>0 равно… Ответ записать в виде
десятичной дроби (округлить до десятых).
Ответ: 0,5
23.НТ1(О). Среднее
количество электронов при Т>0 в одном
квантовом состоянии с энергией
![]() равно… Ответ округлить до десятых.
равно… Ответ округлить до десятых.
Ответ:0,7
24.НТ1(3). Распределение Бозе-Эйнштейна по состояниям – это ...
*А) среднее количество бозонов в одном квантовом состоянии;
В) среднее количество
бозонов с энергией
![]() ;
;
С) вероятность
нахождения бозона с энергией
![]() ;
;
D)
плотность вероятности нахождения бозона
в интервале
![]() .
.
25.НТ1(3). Функция распределения Бозе-Эйнштейна по состояниям имеет вид ...
*А)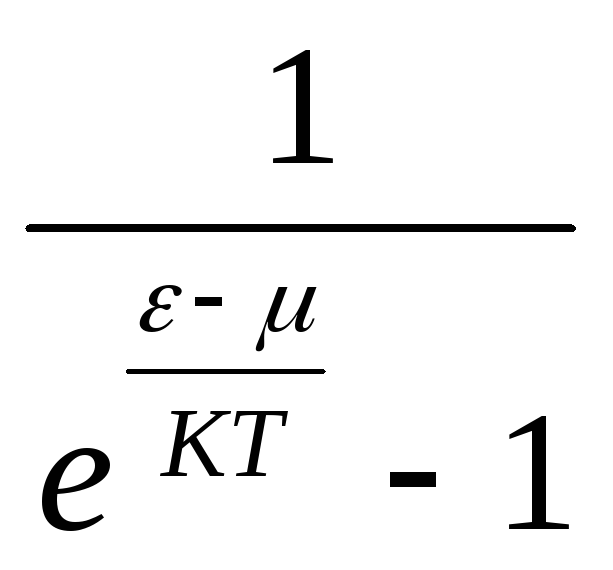 ;
В)
;
В)![]() ;
С)
;
С)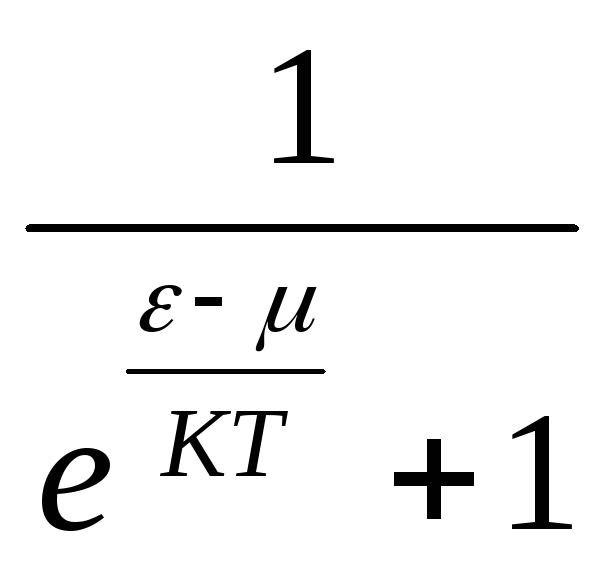 ;
D)
;
D)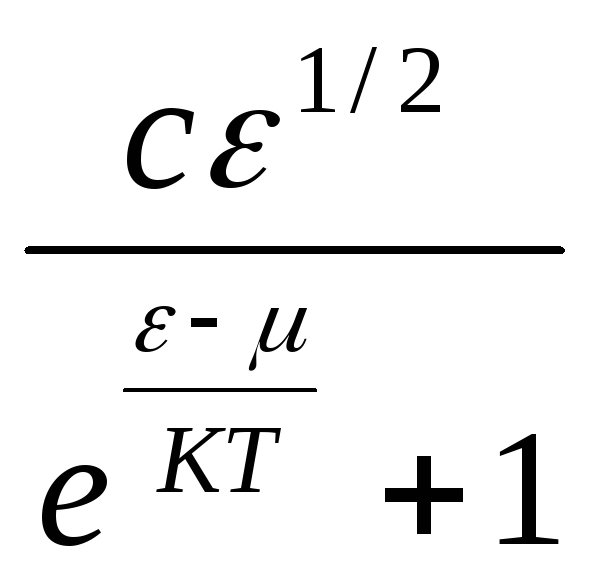 .
.
26.НТ1(3). Функция распределения Бозе-Эйнштейна по состояниям может быть получена путём усреднения по формуле ...
А)
![]() ,
где
,
где
![]() -
вероятность нахождения
-
вероятность нахождения
![]() частиц в K-том
состоянии;
частиц в K-том
состоянии;
*В)
![]() ,
где
,
где
![]() -
то же, что и в пункте А;
-
то же, что и в пункте А;
С)
![]() ,
где
,
где
![]() -
вероятность того, что на K-ом
уровне находится
-
вероятность того, что на K-ом
уровне находится
![]() частиц.
частиц.
D)
![]() ,
где
,
где
![]() -
то же, что и в пункте С.
-
то же, что и в пункте С.
27.НТ1(3). Функция
распределения Бозе-Эйнштейна находится
путём усреднения по формуле
![]() ,
где K
– это …
,
где K
– это …
А) номер энергетического уровня;
*В) набор квантовых чисел, задающих данное квантовое состояние свободного бозона;
С) набор квантовых чисел, задающих данное квантовое состояние электрона в металле;
D) набор квантовых чисел, задающих данное квантовое состояние электрона в атоме.
28.НТ1(3). На рисунке
приведено распределение Бозе-Эйнштейна
для двух температур. Соотношение
температур
![]() …
…![]() .
.
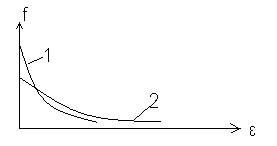
Для кривых выполняется соотношение:
A)
![]() ;
* B)
;
* B)
![]() ;
C)
;
C)
![]() ;
D)
;
D)
![]() .
.
29.НТ1(3). Химический
потенциал системы бозонов
![]()
А)![]() ;
*В)
;
*В)![]() ;
С)
;
С)![]() ;
D)
;
D)![]() .
.
30.НТ1(3). Плотность квантовых состояний в энергетическом пространстве – это ...
А) число состояний
с энергией
![]() ;
;
*В) число состояний в единичном малом интервале энергии;
С) число состояний
в интервале
![]() ,
,![]() ;
;
D)
число состояний в интервале
![]() .
.
31.НТ1(О). Запишите
формулу для количества квантовых
состояний, соответствующих интервалу
![]() и объему V,
используя
шаблон
и объему V,
используя
шаблон
![]()
a
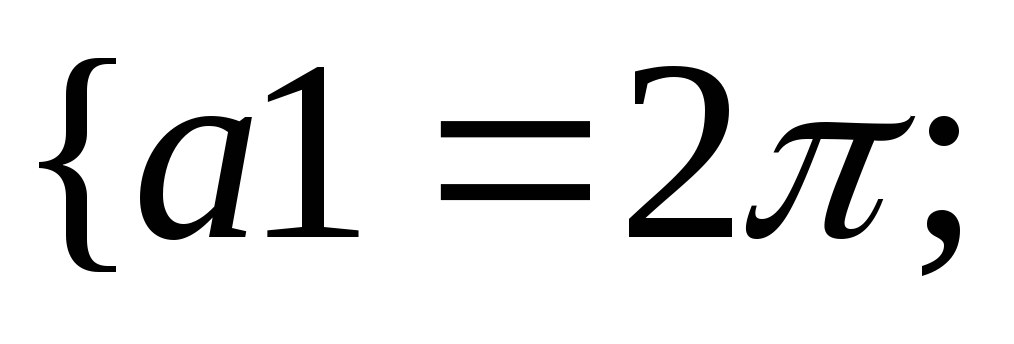
![]()
![]()
b
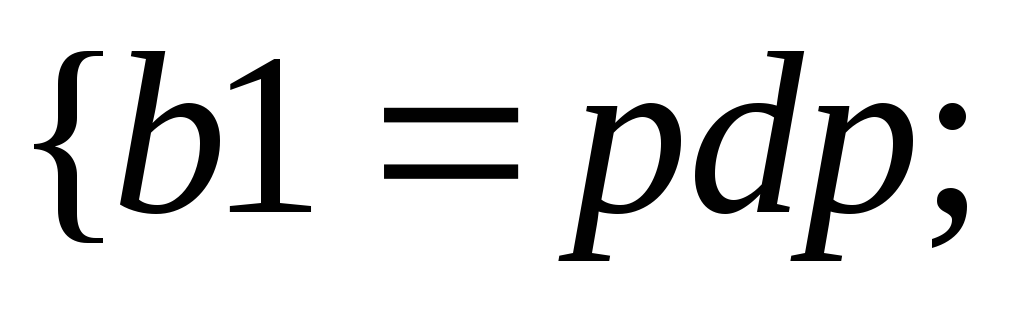
![]()
![]()
c
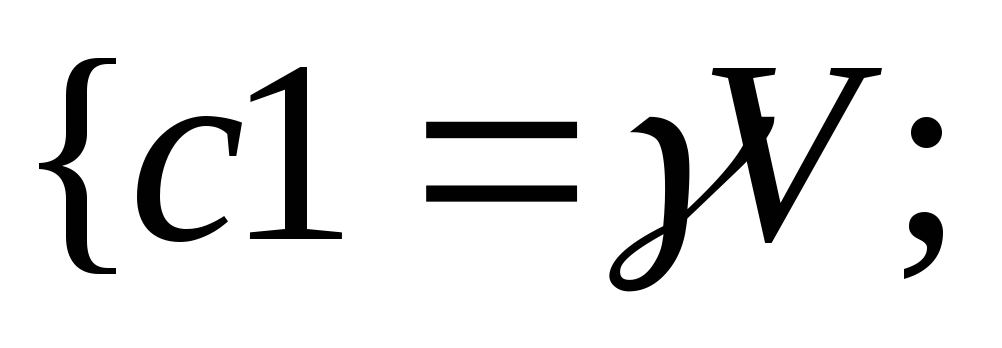
![]()
![]() .
.
Ответ:
![]()
32.HT1(O).
Запишите
формулу, определяющую количество
квантовых состояний для квазисвободных
частиц, находящихся в объеме V
и обладающих импульсами в интервале
![]()
![]()
![]() ,
используя шаблон
,
используя шаблон
![]()
a
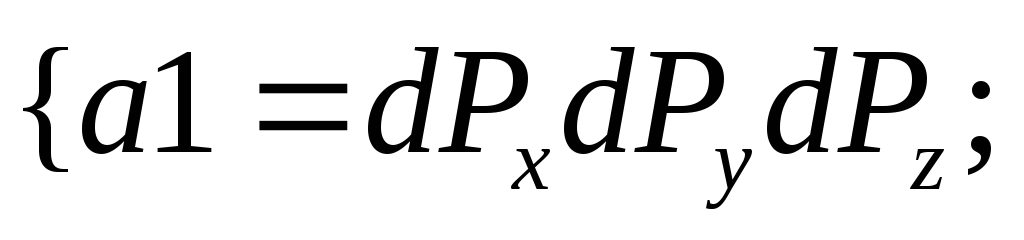
![]()
![]()
b
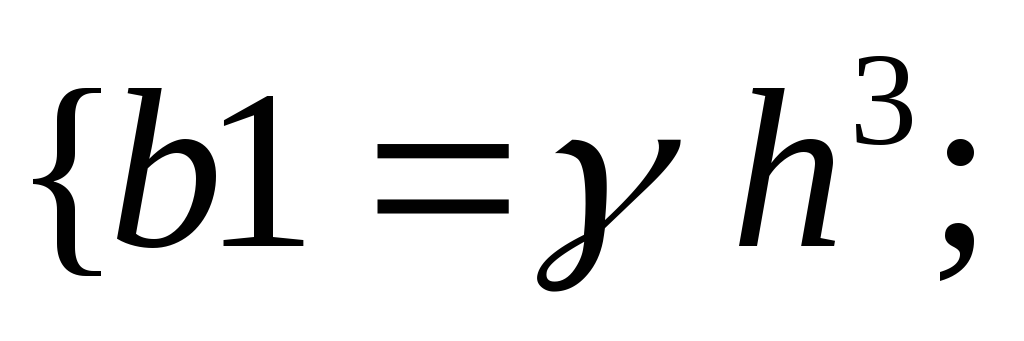
![]()
![]() .
.
Ответ:
![]()
33.НТ1(О). Запишите
формулу для фазового объема, соответствующего
интервалу
![]() и объему V,
используя шаблон
и объему V,
используя шаблон
![]()
a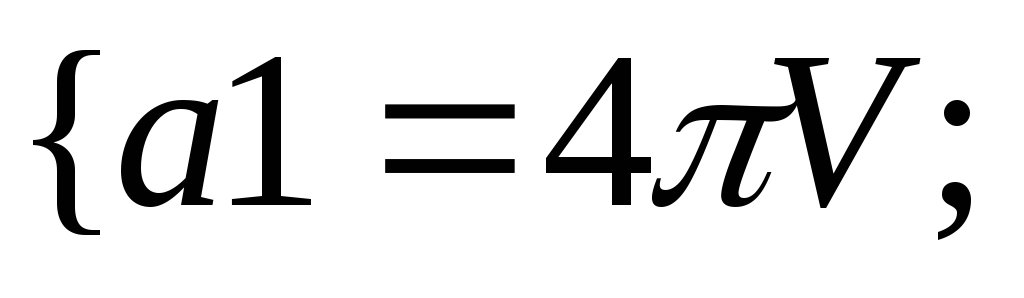
![]()
![]()
b
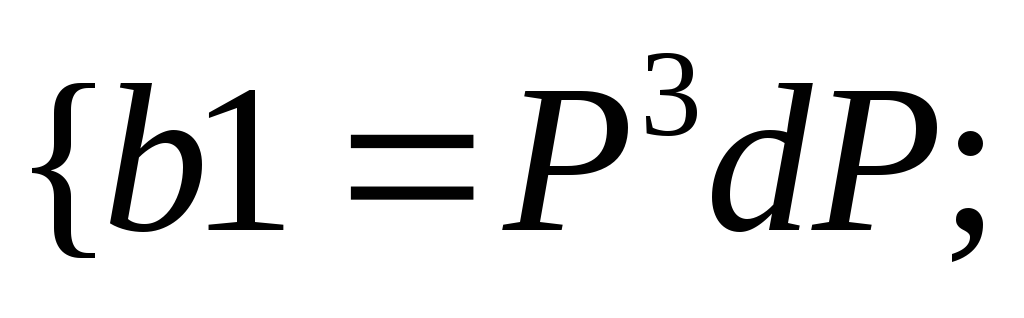
![]()
![]()
Ответ:
![]()
34.НТ1(О). Запишите
формулу для фазового объема, соответствующего
интервалу
![]() и объему V,
используя шаблон
и объему V,
используя шаблон
![]()
a
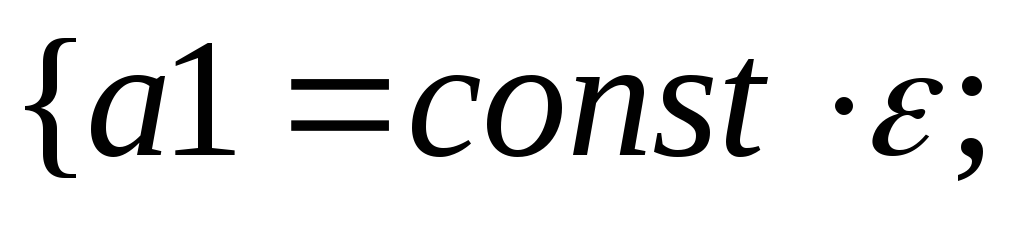
![]()
![]()
b
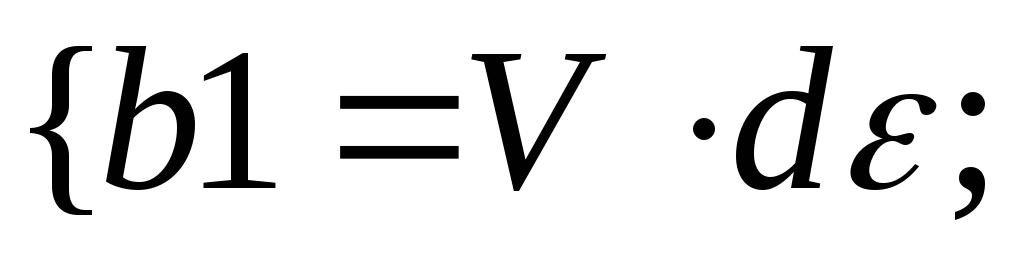
![]()
![]()
Ответ:
![]()
35.НТ1(О). Запишите
формулу для количества квантовых
состояний, соответствующих интервалу
![]() и объему V,
используя шаблон
и объему V,
используя шаблон
![]()
a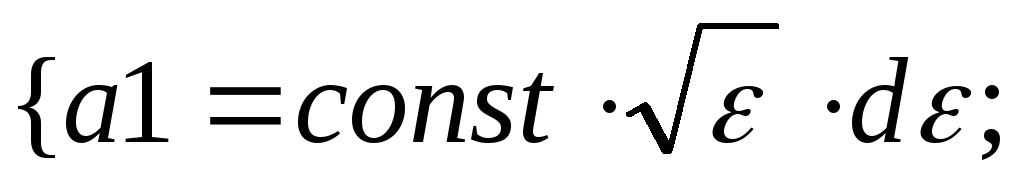
![]()
![]()
b
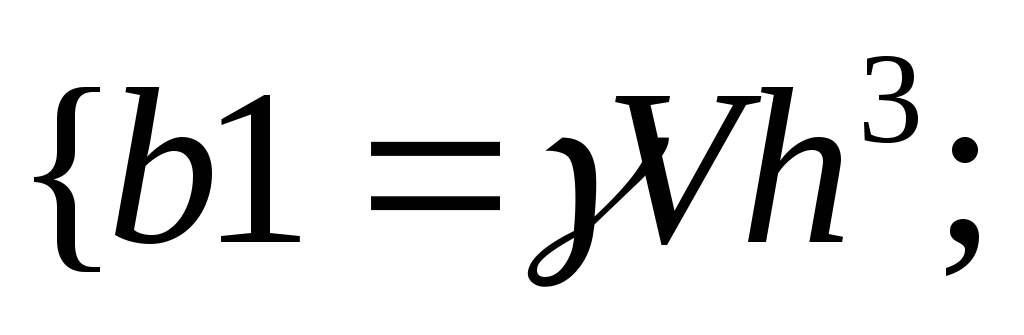
![]()
![]()
Ответ:
![]()
36.НТ1(О). Запишите
формулу для фазового объема, соответствующего
интервалу модуля скорости
![]() и объему V,
используя шаблон
и объему V,
используя шаблон
![]()
a
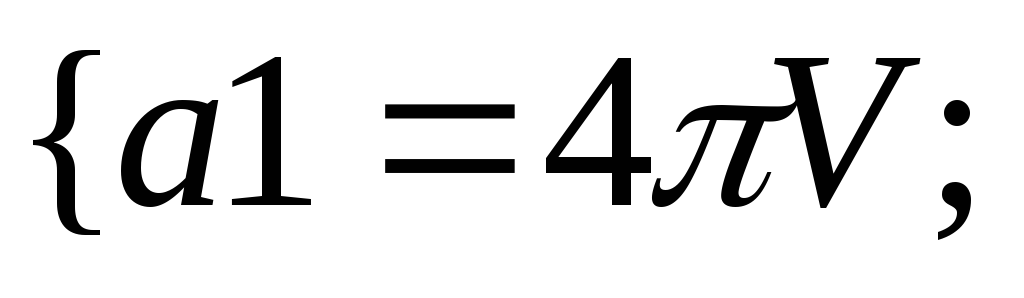
![]()
![]()
b
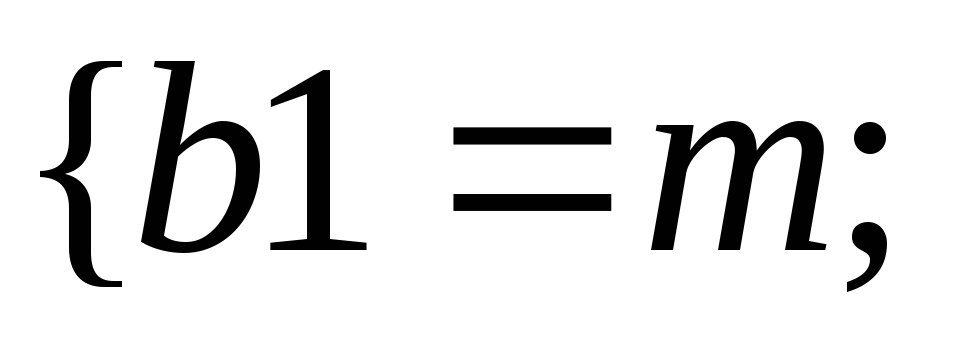
![]()
![]()
c
![]()
![]()
![]() .
.
Ответ:
![]() c2
c2
37.НТ1(О). Запишите
формулу для количества квантовых
состояний, соответствующих интервалу
модуля скорости
![]() и объему V,
используя шаблон
и объему V,
используя шаблон
![]()
a

![]()
![]()
b
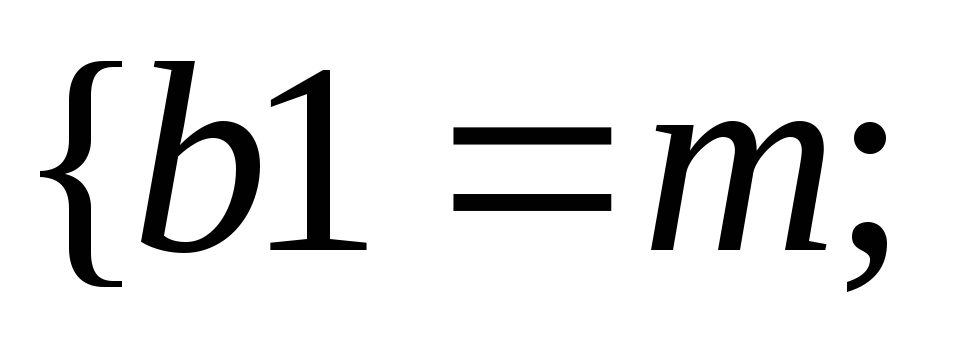
![]()
![]()
c
![]()
![]()
![]() .
.
Ответ:
![]()
38.НТ1(О). Запишите
формулу для плотности состояний,
используя шаблон
![]()
a
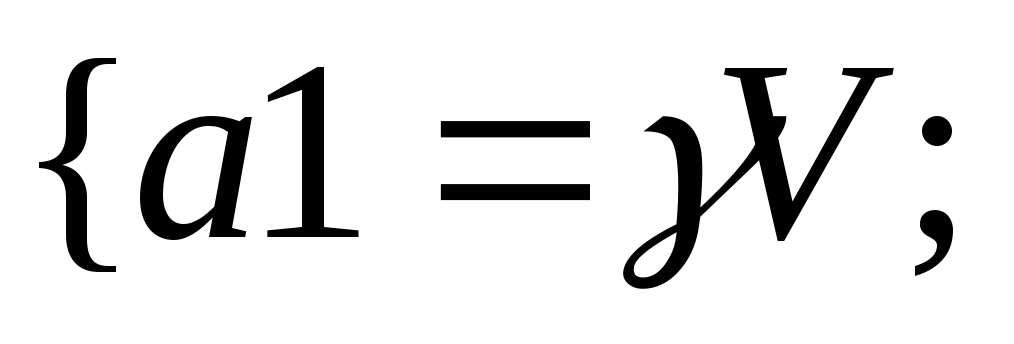
![]()
![]()
b
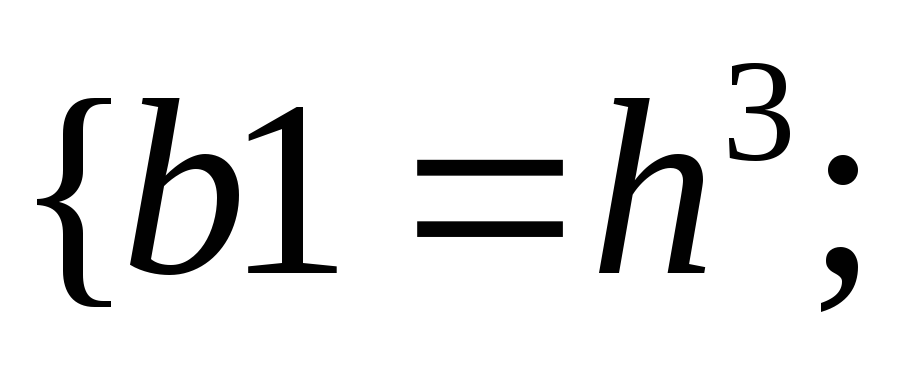
![]()
![]() .
.
Ответ:
![]()
39.НТ1(О). Запишите
формулу для плотности состояний,
используя шаблон
![]()
a
![]()
![]()
![]()
b
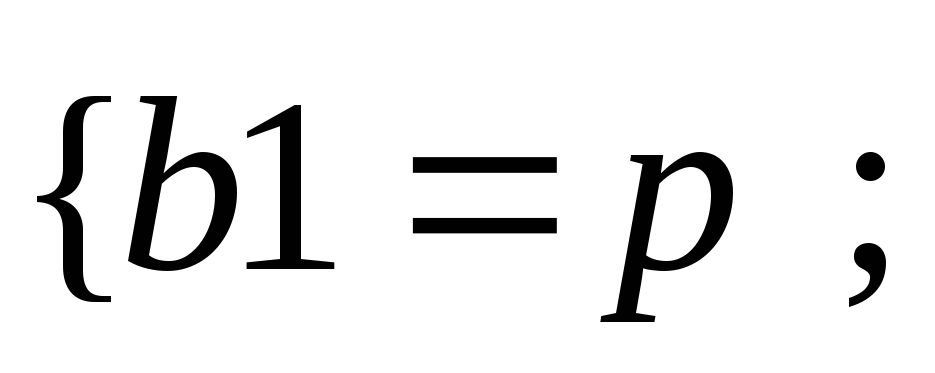
![]()
![]() .
.
c
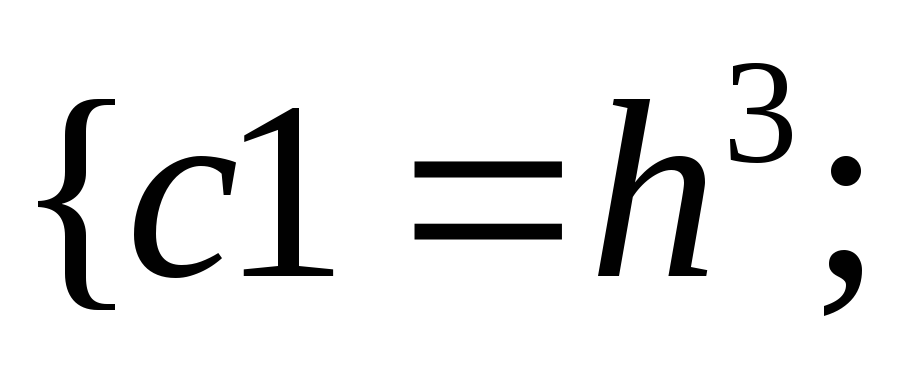
![]()
![]() .
.
Ответ:
![]()
40.НТ1(О). Запишите
формулу для плотности состояний,
используя шаблон
![]()
a
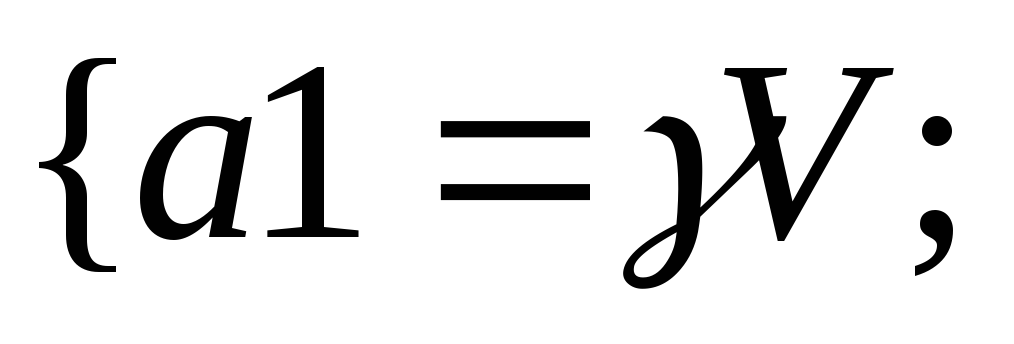
![]()
![]()
b
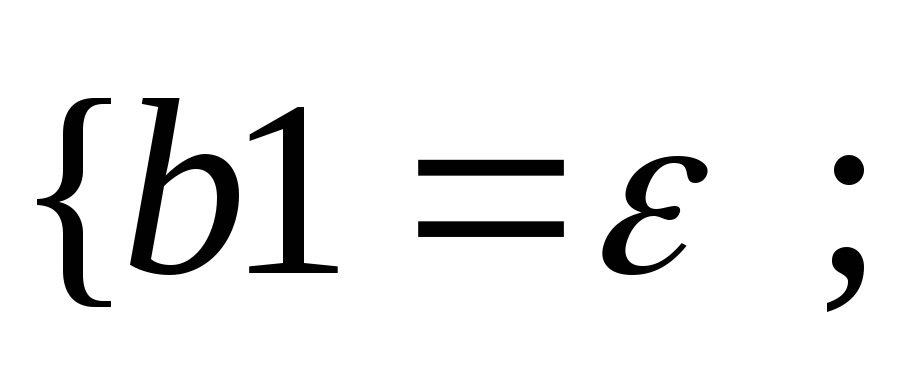
![]()
![]() .
.
c
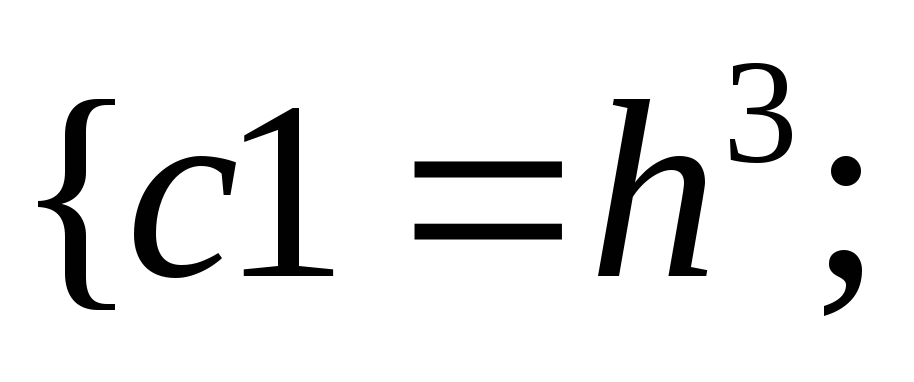
![]()
![]() .
.
Ответ:
![]()
41.НТ1(О). Запишите
формулу для плотности состояний в
зависимости от модуля скорости, используя
шаблон
![]()
a
![]()
![]()
![]()
b
![]()
![]()
![]() .
.
c
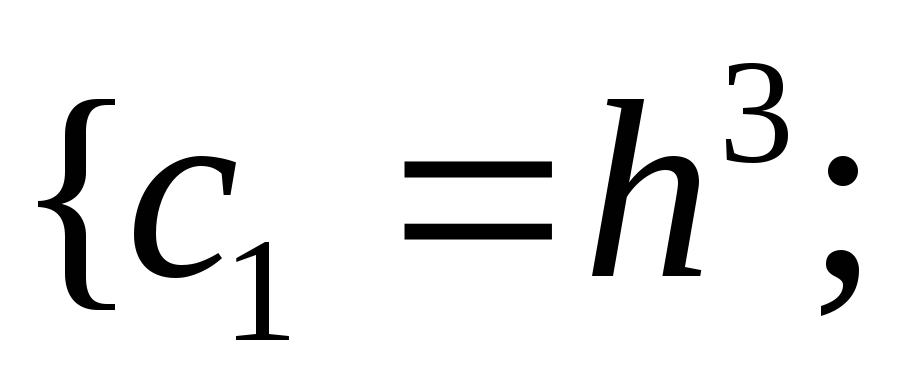
![]()
![]() .
.
Ответ:
![]()
42.НТ1(О). Запишите
формулу для среднего количества фермионов
в одном квантовом состоянии при заданной
энергии ε,
используя шаблон
![]()
a {![]()
![]()
![]() };
};
b {![]()
![]()
![]() };
};
@ ={+;
-; /}.
={+;
-; /}.
Ответ:
![]()
43.НТ1(О). Запишите
формулу для распределения Ферми-Дирака
по состояниям, используя шаблон
![]()
a {![]()
![]()
![]() };
};
b {![]()
![]()
![]() };
};
@ ={+;
-; /}.
={+;
-; /}.
Ответ:
![]()
44.НТ1(О). Запишите
формулу для среднего количества бозонов
в одном квантовом состоянии, используя
шаблон
![]()
a {![]()
![]()
![]() };
};
b {![]()
![]()
![]() };
};
@ ={+;
-; /}.
={+;
-; /}.
Ответ:
![]()
45.НТ1(О). Запишите
формулу для распределения Бозе-Эйнштейна
по состояниям, используя шаблон
![]()
a {![]()
![]()
![]() };
};
b {![]()
![]()
![]() };
};
@ ={+;-;/}.
={+;-;/}.
Ответ:
![]()
46.НТ1(3). Функция распределения частиц по энергиям в квантовой статистике – это …
А) среднее число
частиц с энергией
![]() ;
;
*В) среднее число частиц в малом единичном интервале энергии;
С) среднее число
частиц в одном квантовом состоянии с
энергией
![]() ;
;
D)
вероятность нахождения частицы с
энергией
![]() .
.
47.НТ1(3). Функция распределения частиц по энергиям в квантовой статистике определяется по формуле …
*А)
![]() ;
В)
;
В)
![]() ;
;
С)
![]() ;
D)
;
D)
![]() .
.
48.НТ1(3). Функция распределения Ферми-Дирака по энергиям имеет вид...
А)
![]() ;
*B)
;
*B)
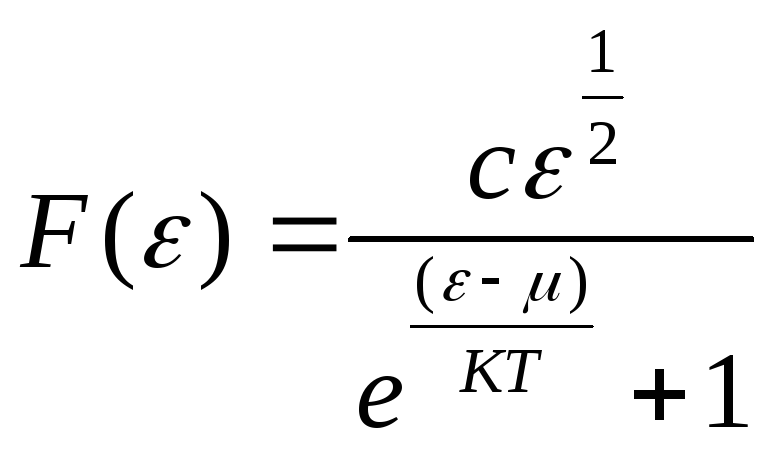 ;
;
С)
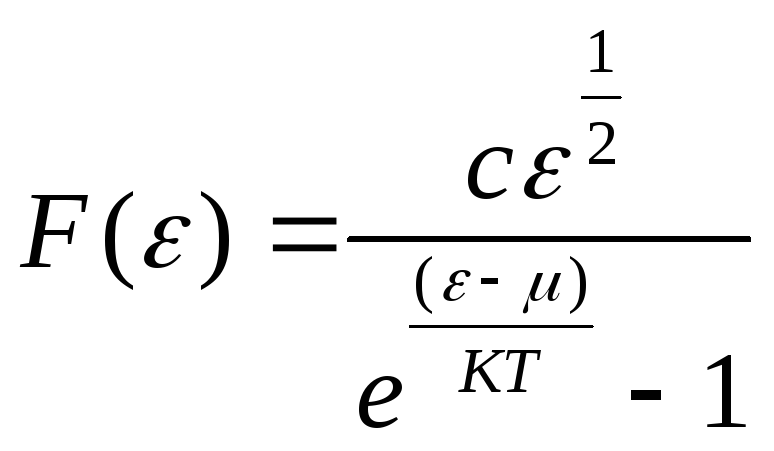 ;
D)
;
D)
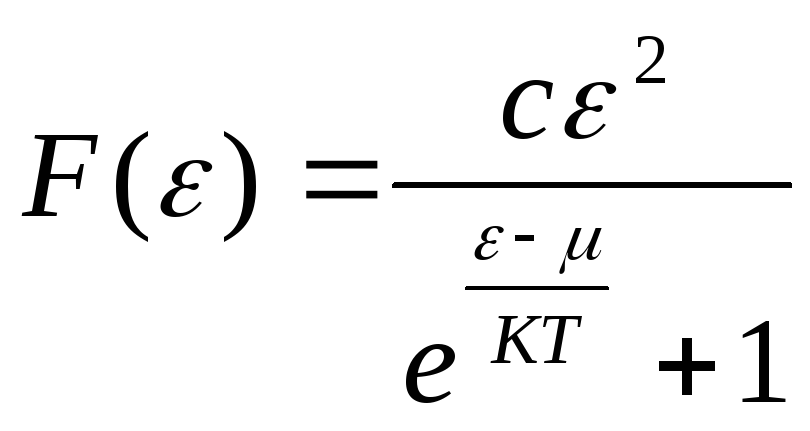 .
.
49.НТ1(3). Функция распределения Ферми-Дирака по энергиям при Т=0 представлена на рисунке...
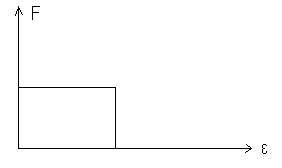
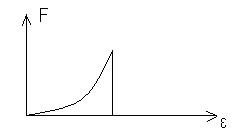 А)
В)
А)
В)
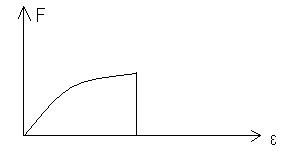
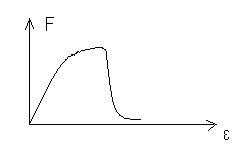 *С)
D)
*С)
D)
50.НТ1(3). На рисунке изображена функция распределения Ферми-Дирака по энергиям при разных температурах.
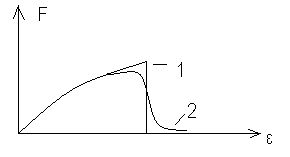
Кривая 1 соответствует Т1
Кривая 2 соответствует Т2
А) Т1=0; Т2=0;
В) Т1>0; Т2=0;
*С) Т1=0; Т2>0;
D) Т1>0; Т2>0.
51.НТ1(3). Для
распределения Ферми-Дирака по энергии
выражение
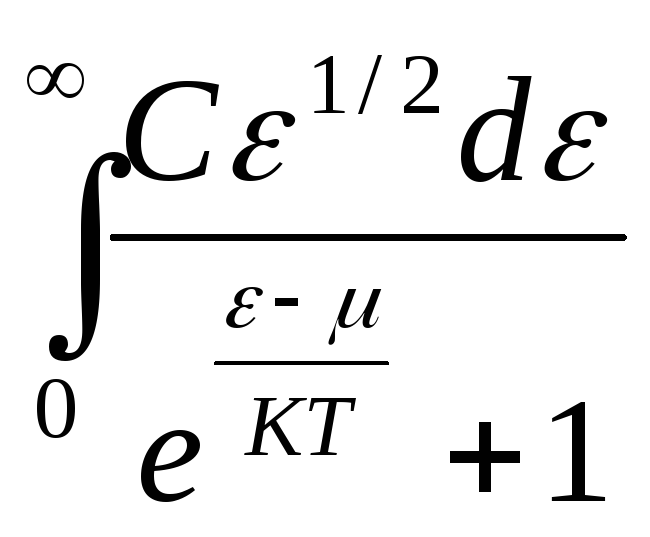 имеет смысл …
имеет смысл …
А) средняя энергия фермионов при Т=0;
*В) число частиц в
интервале
![]() ;
;
С) общая энергия всей системы фермионов;
D) средняя энергия фермионов при Т>0.
52.НТ1(3). Для
распределения Ферми-Дирака по энергии
выражение
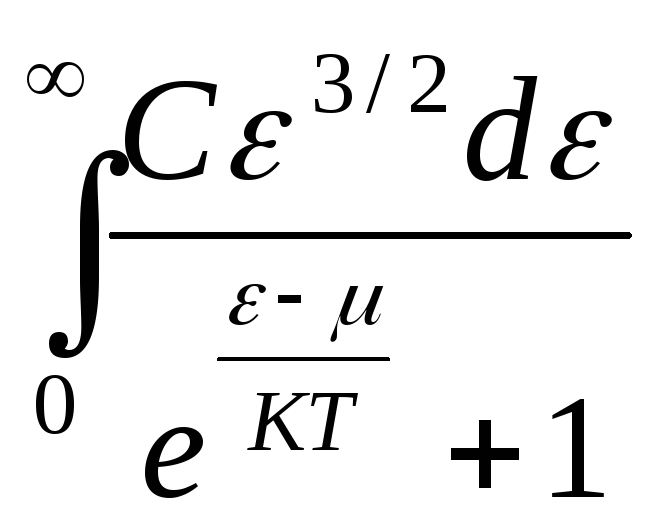 имеет смысл …
имеет смысл …
А) средняя энергия фермионов при Т=0;
В) средняя энергия фермионов при Т>0;
*С) общая энергия всей системы фермионов;
D) общее число фермионов в системе.
53.НТ1(3). Энергия Ферми – это …
*А) максимальная энергия фермионов при Т=0;
В) средняя энергия фермионов при Т=0;
С) средняя энергия фермионов при Т>0;
D) потенциальная энергия фермиона.
54.НТ1(3). Функция распределения Ферми-Дирака по модулю квазиимпульса равна …
*А)
![]() ;
В)
;
В)
![]() ;
;
С)
![]() ;
D)
;
D)
![]() .
.
55.НТ1(3). Функция распределения Ферми-Дирака по модулю импульса при Т=0 представлена на рисунке …
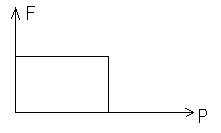
A) *B)
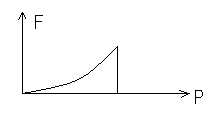
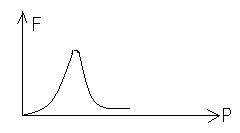
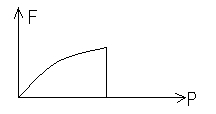
C) D)
56.НТ1(3). На рисунке изображена функция распределения Ферми-Дирака по модулю импульса при разных температурах.

Кривая 1 соответствует Т1
Кривая 2 соответствует Т2
А) Т1=0; Т2=0;
В) Т1>0; Т2=0;
*С) Т1=0; Т2>0;
D) Т1>0; Т2>0.
57.НТ1(О). Энергия
Ферми
![]() ,
средняя энергия фермионов при Т=0
,
средняя энергия фермионов при Т=0
![]() .
.
Отношение
![]() ... Округлить до десятых.
... Округлить до десятых.
Ответ: 0,6
58.НТ1(3). Распределение Бозе-Эйнштейна по энергиям – это …
А) среднее число
бозонов с энергией
![]() ;
;
В) среднее число
бозонов в одном квантовом состоянии с
энергией
![]() ;
;
*С) среднее число бозонов в единичном малом интервале энергии;
D) вероятность нахождения бозона в единичном интервале энергии.
59.НТ1(3). Функция распределения Бозе-Эйнштейна по энергиям имеет вид ...
А)
![]() ;
*В)
;
*В)
 ;
;
С)
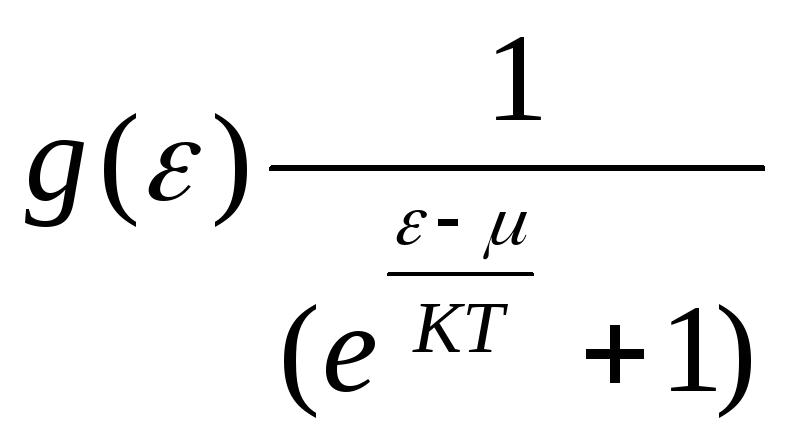 ;
D)
;
D)
![]() .
.
60.НТ1(3). Распределение Больцмана по состояниям имеет вид ...
А)
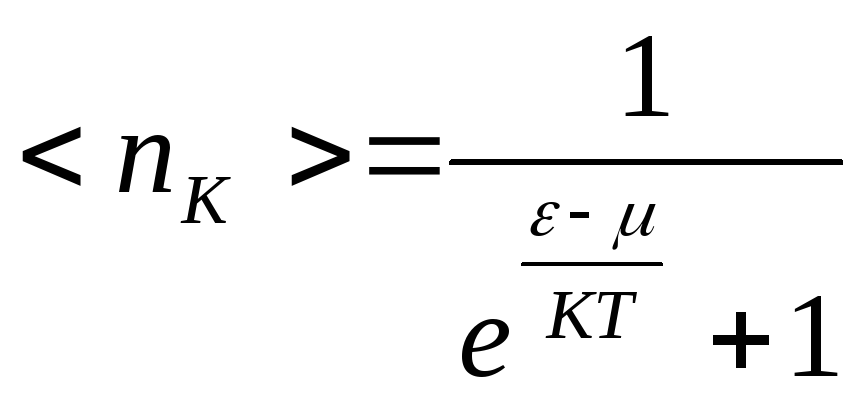 ;
В)
;
В)
 ;
;
*С)
![]() ;
D)
;
D)
![]() .
.
61.НТ1(3). Распределение Больцмана по состояниям применимо при условии …
А)
![]() ;
*В)
;
*В)
![]() ;
С)
;
С)
![]() ;
D)
;
D)
![]() .
.
62.НТ1(3).Распределение
Больцмана
![]() применимо для ...
применимо для ...
А) фермионов;
В) бозонов;
*С) систем частиц малой плотности, у которых не проявляются квантовые свойства;
D) для вырожденных систем.
63.НТ1(С). Для каждой функции распределения выберите все соответствия.
А)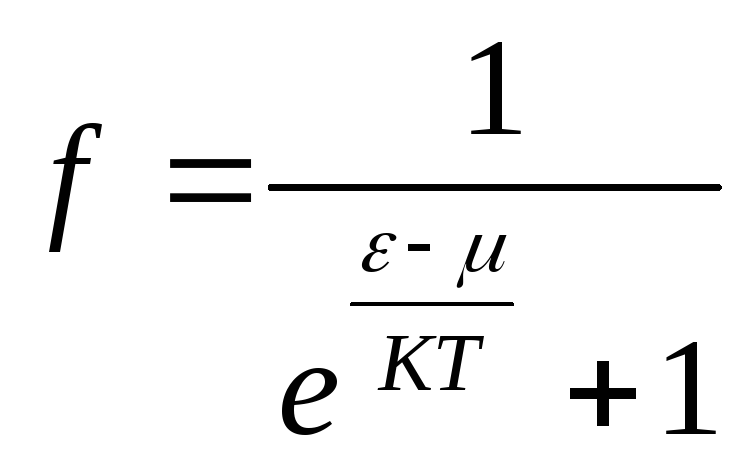 А) Вырожденная система
фермионов;
А) Вырожденная система
фермионов;
В)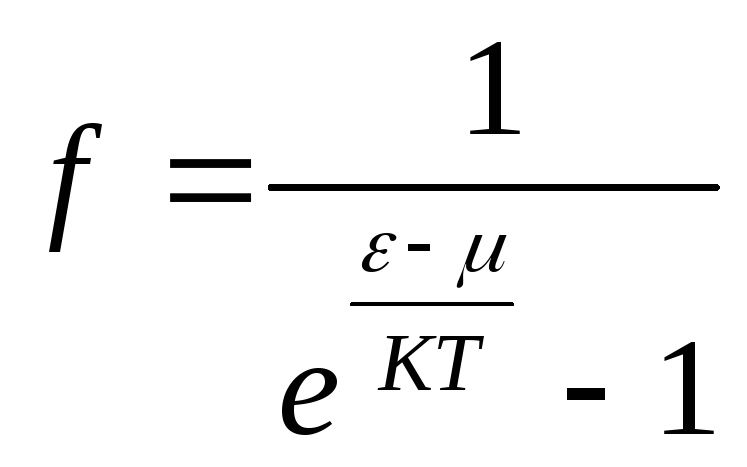 В) Система частиц с целым
спином;
В) Система частиц с целым
спином;
С)![]() С) Вырожденная система
бозонов;
С) Вырожденная система
бозонов;
D) Система частиц с полуцелым спином;
Е) Невырожденная система частиц;
F) Частицы, для которых квантовые
Свойства не проявляются;
G)
Система частиц при
![]() (вырождения);
(вырождения);
H)
Система частиц при
![]() (вырождения).
(вырождения).
Ответ: AA, AD, AH, BB, BC, BH, CE, CF, CG
64.НТ1(3). В интервале
![]() число квантовых состояний
число квантовых состояний![]() ,
число частиц
,
число частиц
![]() .
Для невырожденной системы выполняется
условие
.
Для невырожденной системы выполняется
условие
A)
![]() B)
B)
![]() *C)
*C)
![]() D)
D)
![]() .
.
65.HT1(3).
Для невырожденной системы среднее
количество частиц в одном квантовом
состоянии
![]() равно
равно
A)
 ;
B)
;
B)
 ;
;
*C)
![]() ; D)
; D)
![]() .
.
66.НТ1(3). Температура
вырождения системы
![]() .
Для невырожденной системы выполняется
условие ...
.
Для невырожденной системы выполняется
условие ...
*A)
![]() B)
B)
![]() C)
C)
![]() D)
D)
![]() .
.
67.НТ1(3). Длина волны
де Бойля![]() ,
среднее расстояние между частицами l.
Для невырожденной системы выполняется
условие ...
,
среднее расстояние между частицами l.
Для невырожденной системы выполняется
условие ...
A)
![]() *B)
*B)
![]() C)
C)
![]() D)
D)
![]() .
.
68.HT1(3). Если свойства системы частиц сильно зависят от квантовых свойств частиц, система является ...
A) классической; *B) вырожденной;
C) невырожденной; D) определить нельзя.
69.НТ1(С). Для каждого типа частиц выберите их характеристики:
|
А) Фотон B) Электрон |
A)
масса
покоя
|
|
B)
масса покоя
|
|
|
C)
|
|
|
D)
|
|
|
E)
|
|
|
F)
|
|
|
G) спиновое квантовое число S=1 |
|
|
H) спиновое квантовое число S=1/2 |
Ответ: QAA, AC, AE, AG, BB, BD, BF, BH
70.НТ1(3). На рисунке приведено распределение Ферми-Дирака по энергиям. Площадь заштрихованной области соответствует ...
F
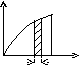
ε
dε
A)
числу частиц с энергией
![]() ;
;
*B)
числу частиц, энергия которых находится
в интервале
![]() ;
;
С) вероятности
того, что энергия частицы находится в
интервале
![]() ;
;
D)
относительному числу частиц в интервале
![]()
71.НТ1(О). Запишите
функцию распределения по состояниям
для электронов в металле, используя
шаблон
![]()
a {![]()
![]()
![]() };
};
b {![]()
![]()
![]() };
};
@ ={+;
-; /}.
={+;
-; /}.
Ответ:
![]()
72. НТ1(3). Если электронный газ находится в невырожденном состоянии, график функции распределения по состояниям имеет вид:
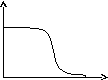 f
A)
f
A) 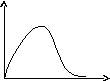 f
B)
f
B)
ε ε

 f
*C) f
D)
f
*C) f
D)
ε ε

 ;
;  ;
; ;
;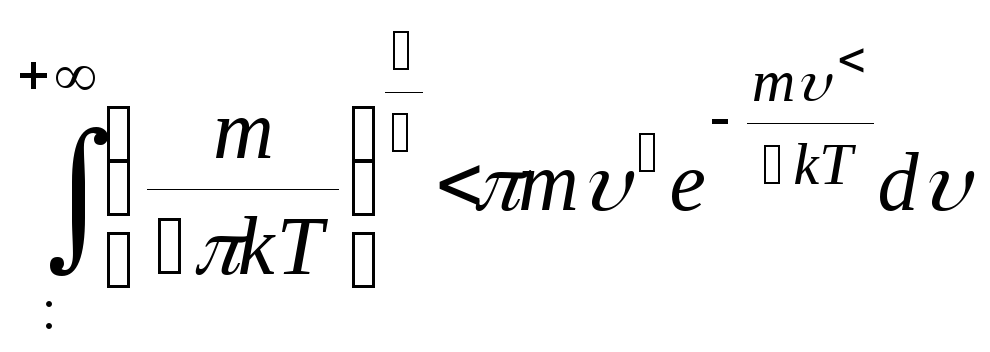
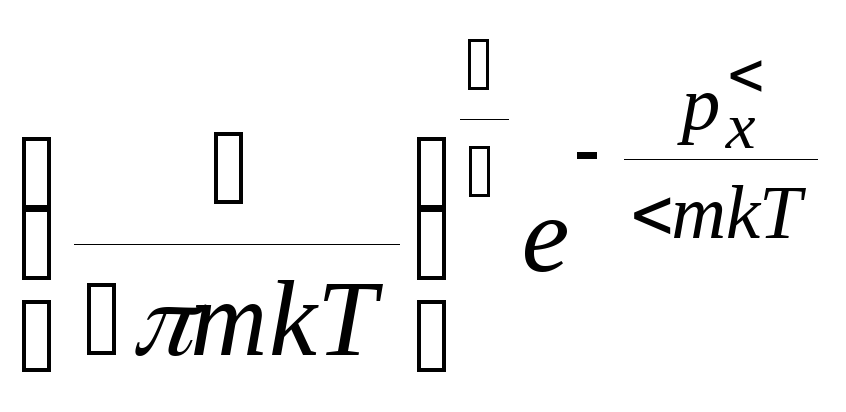 является:
является: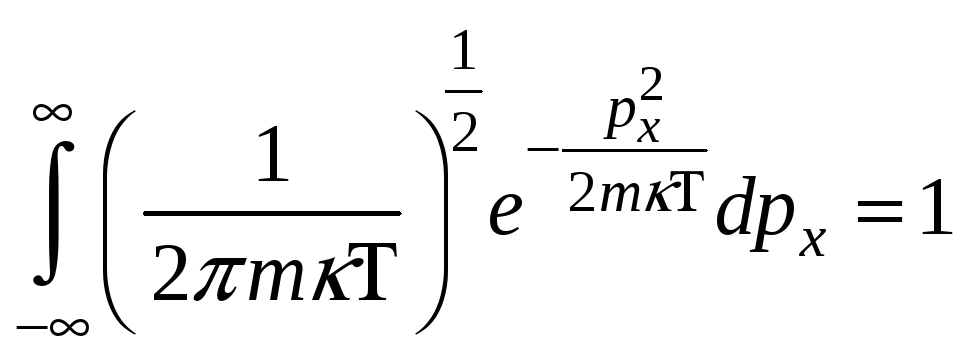

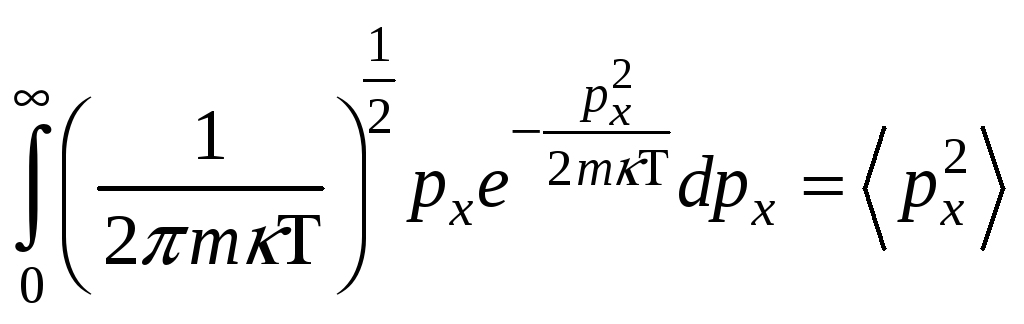
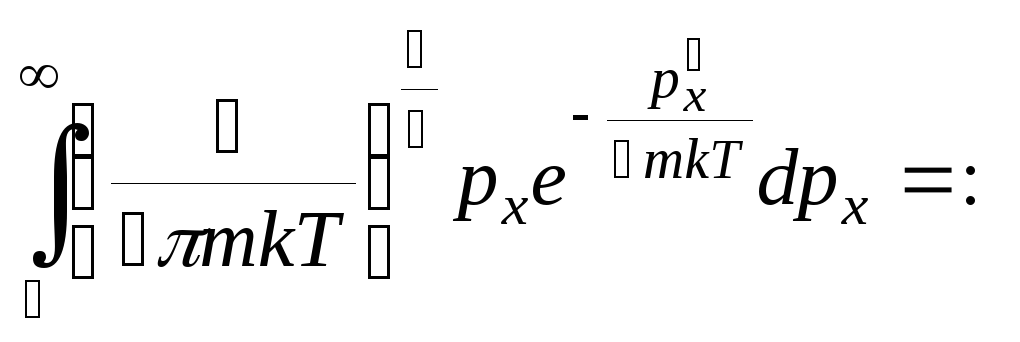
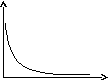
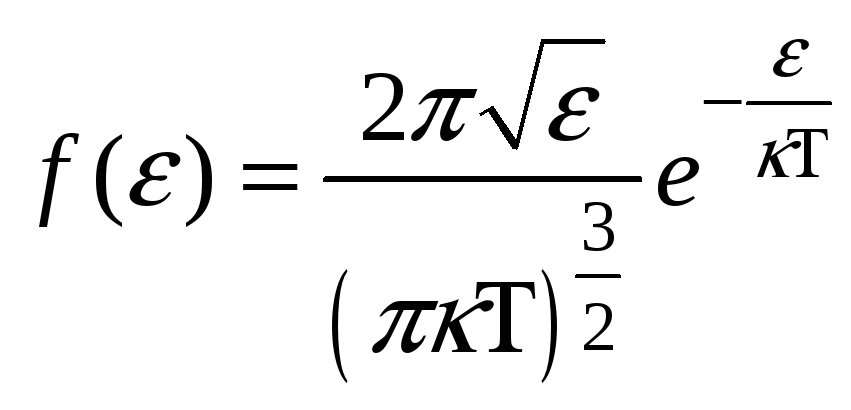 - плотность вероятности или функция
распределения молекул идеального
газа по энергии. Среднее значение
- плотность вероятности или функция
распределения молекул идеального
газа по энергии. Среднее значение
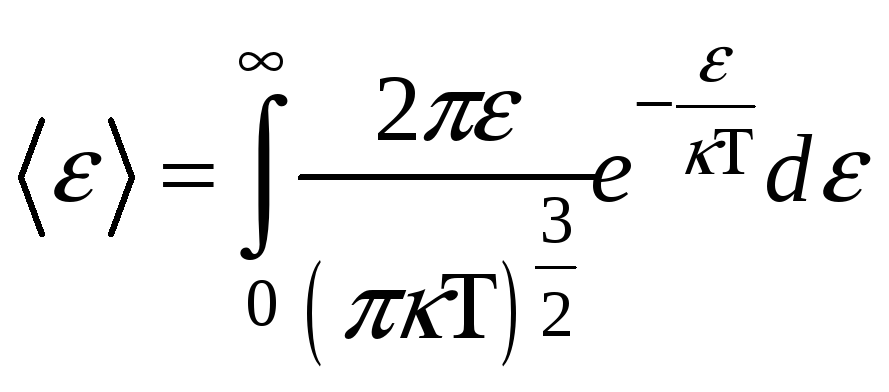 ;
;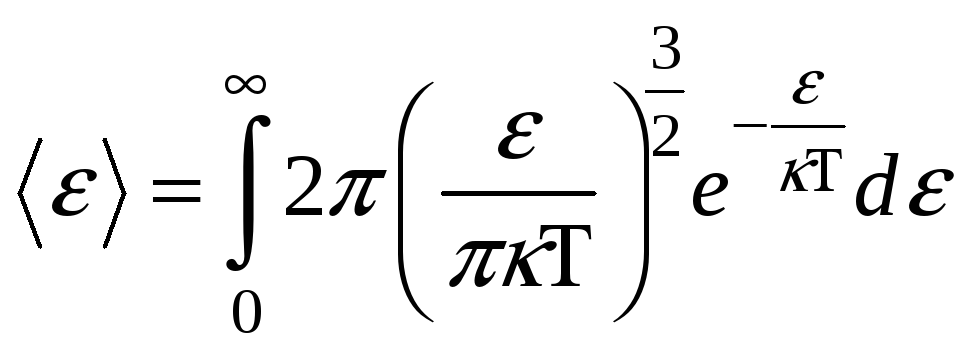 ;
; ;
;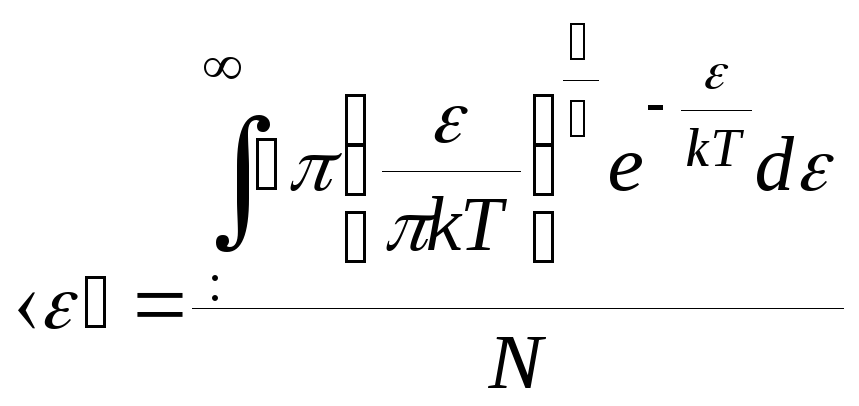 ,
где N
– число частиц.
,
где N
– число частиц.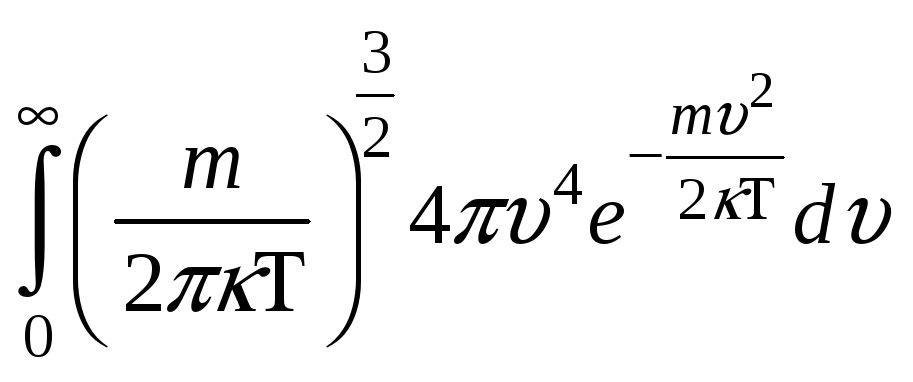 ;
;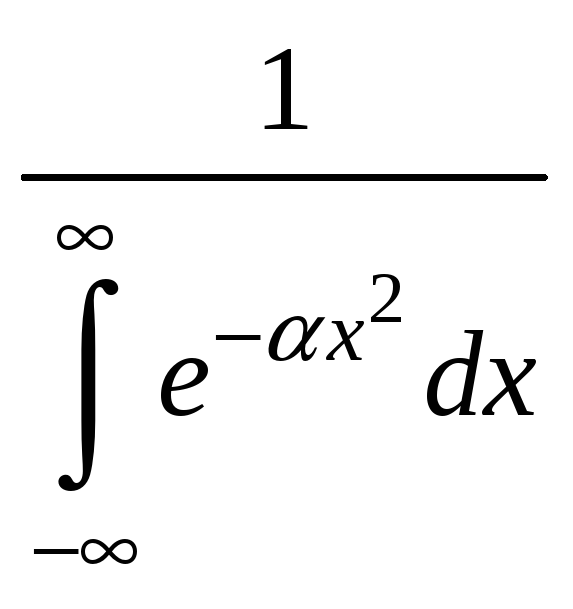 .
.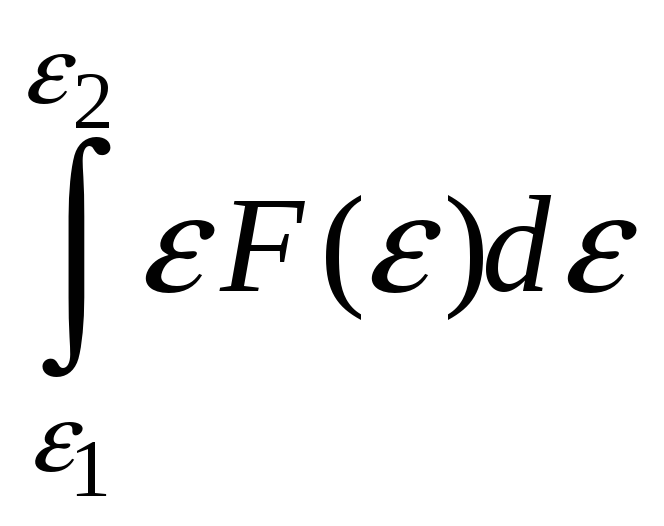 равен:
равен: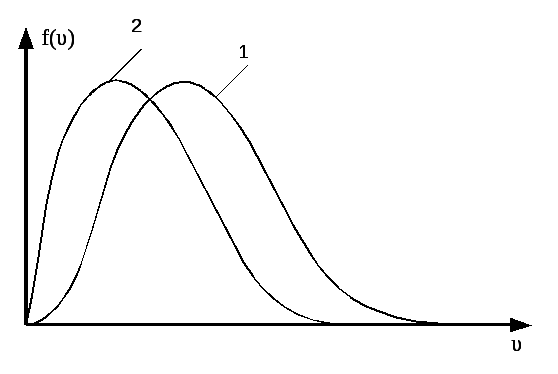



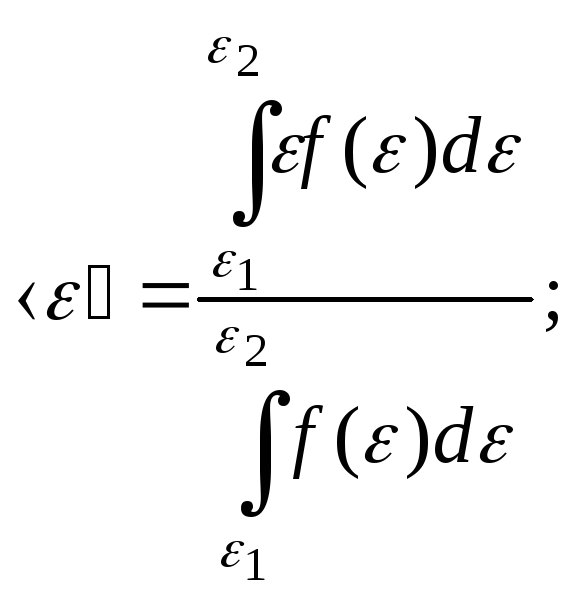
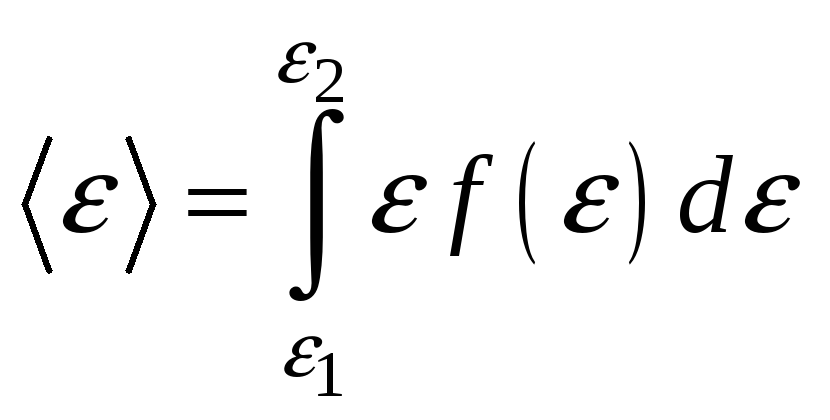 ;
;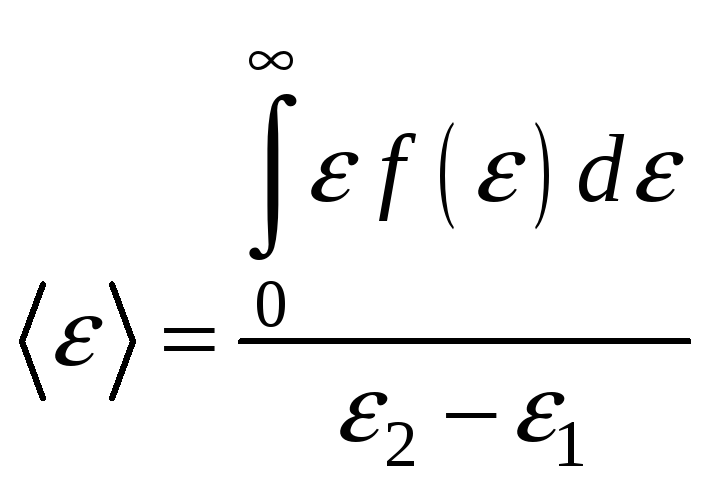 ;
;
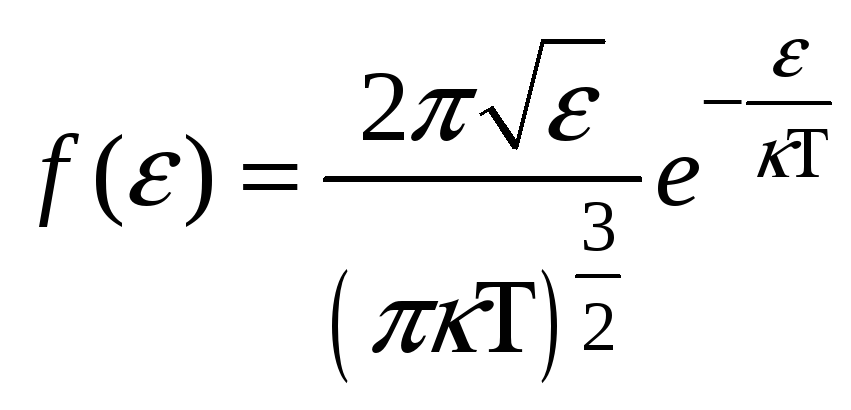 - функция распределения молекул
идеального газа по энергии, которая
удовлетворяет любому соотношению,
кроме:
- функция распределения молекул
идеального газа по энергии, которая
удовлетворяет любому соотношению,
кроме: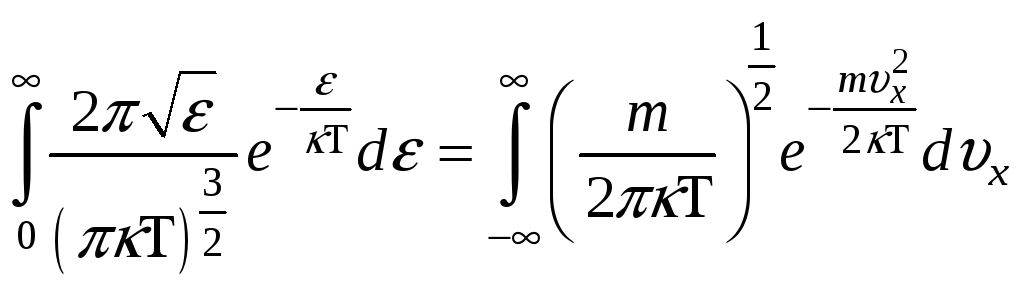 ;
;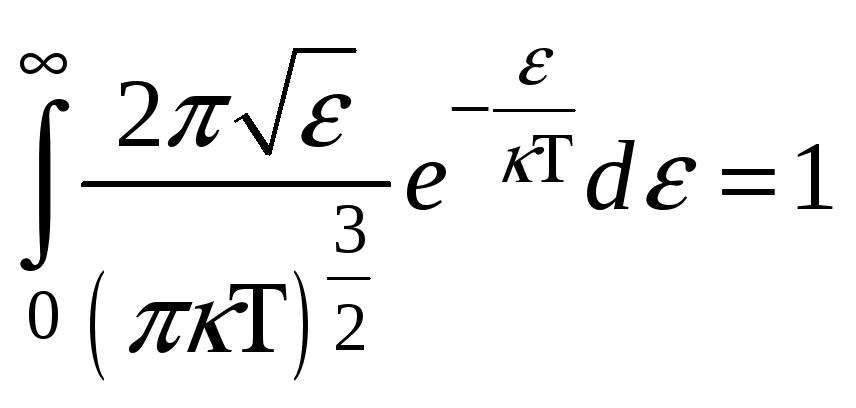 ;
;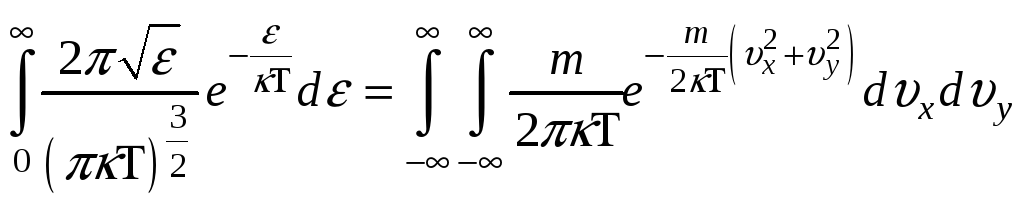 ;
; .
.
 ;
;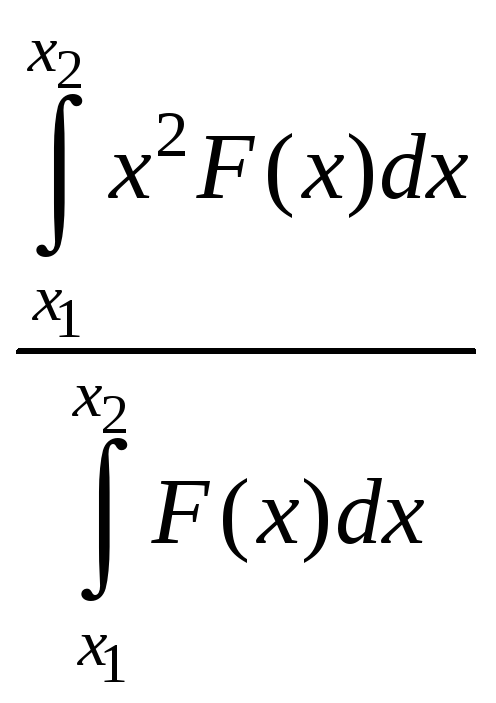 ;
;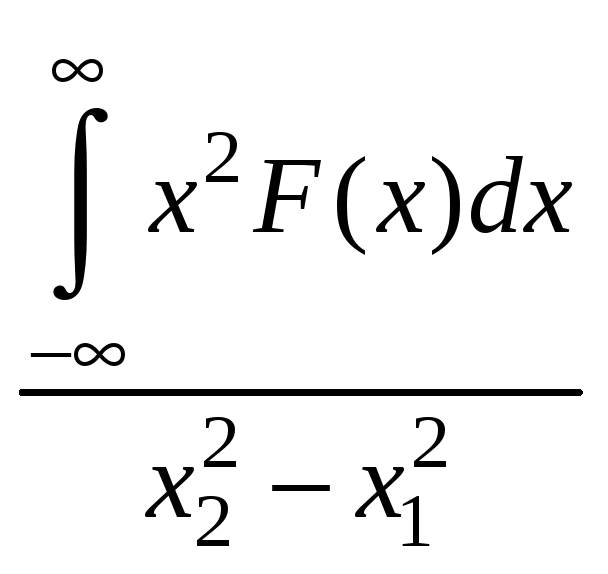 ;
;
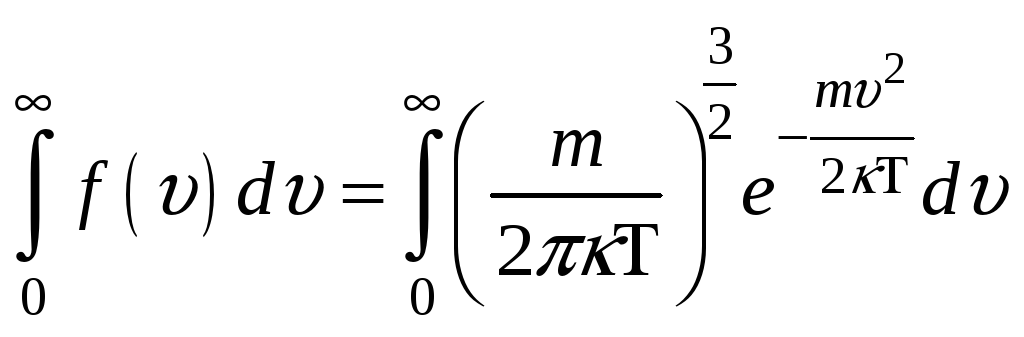 ;
;

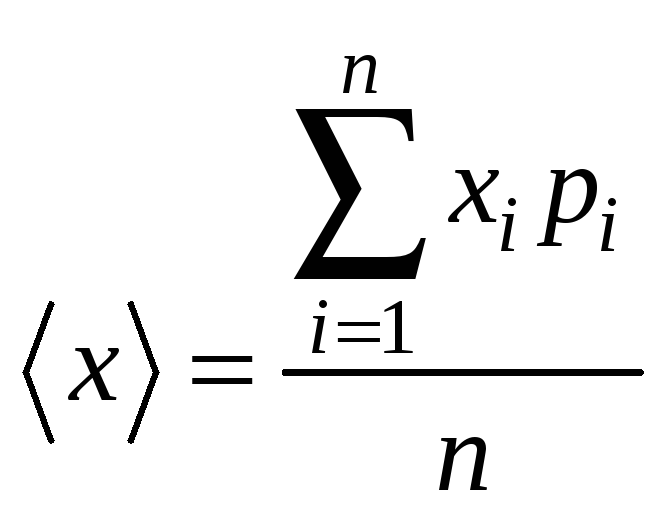 ;
;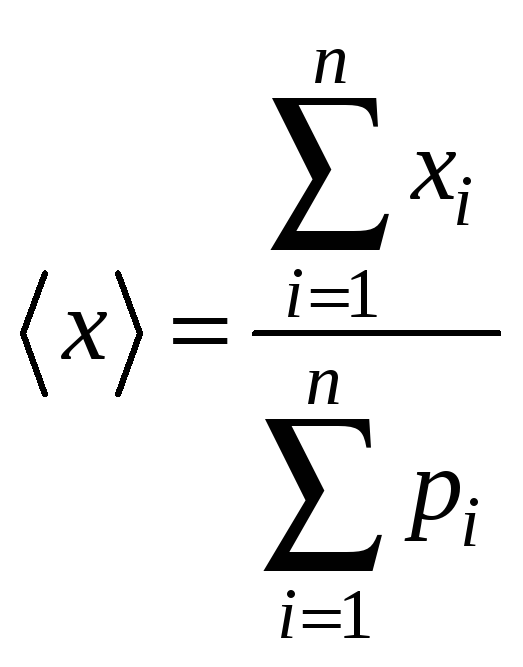
 равно:
равно: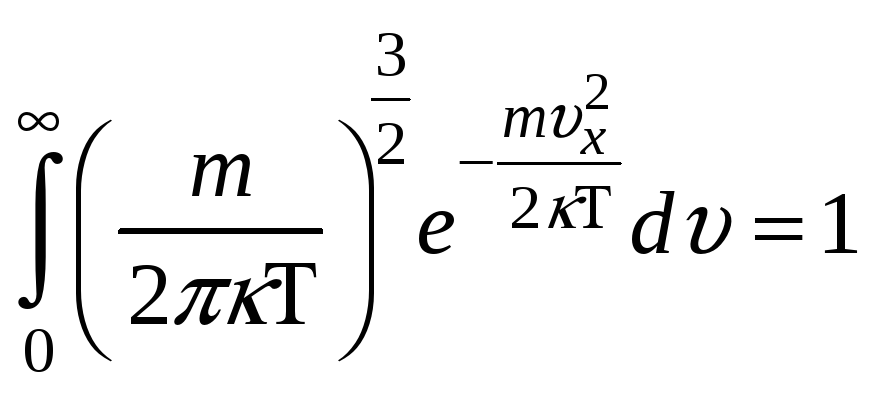 ;
; ;
;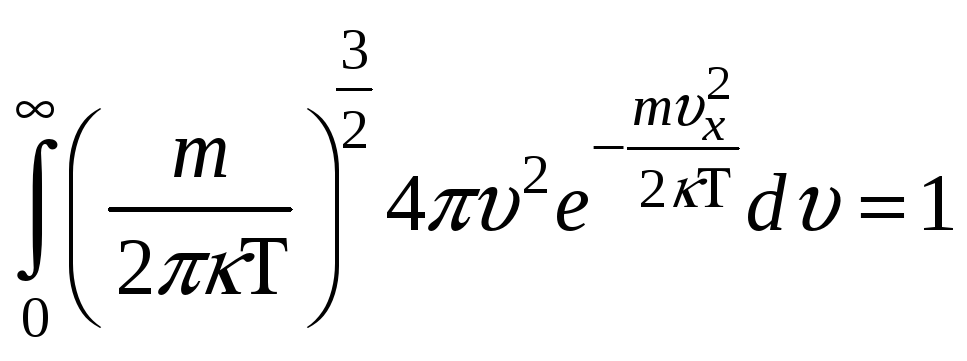 ;
;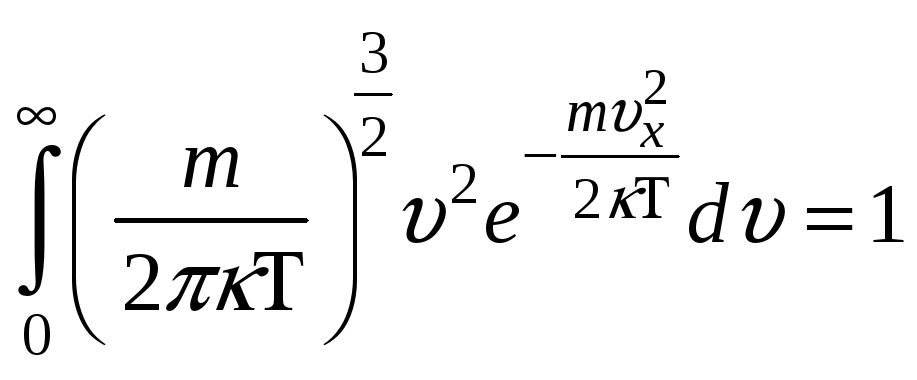
 ;
;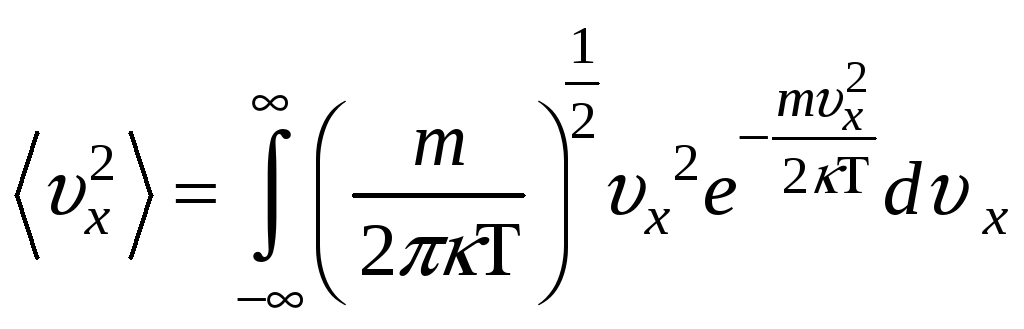 ;
;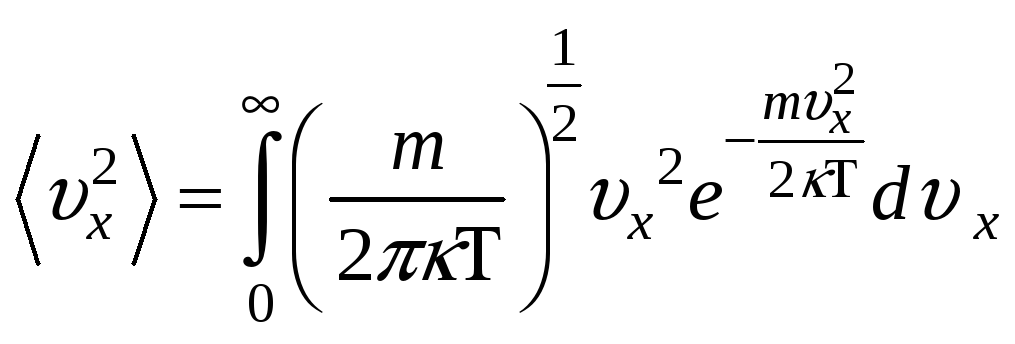 ;
;
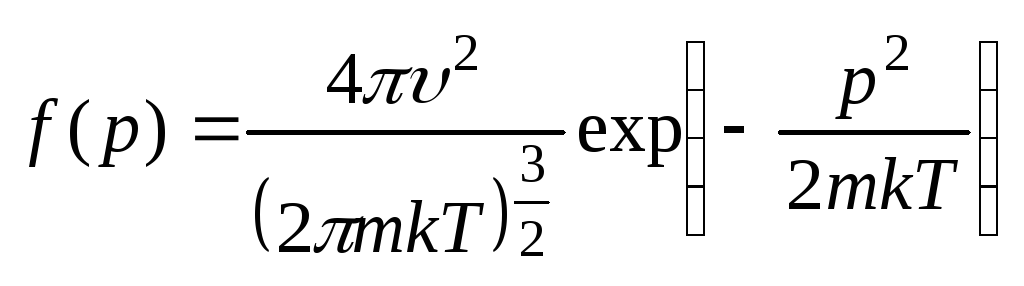 к функции
распределения по модулю скорости
f(u):
к функции
распределения по модулю скорости
f(u):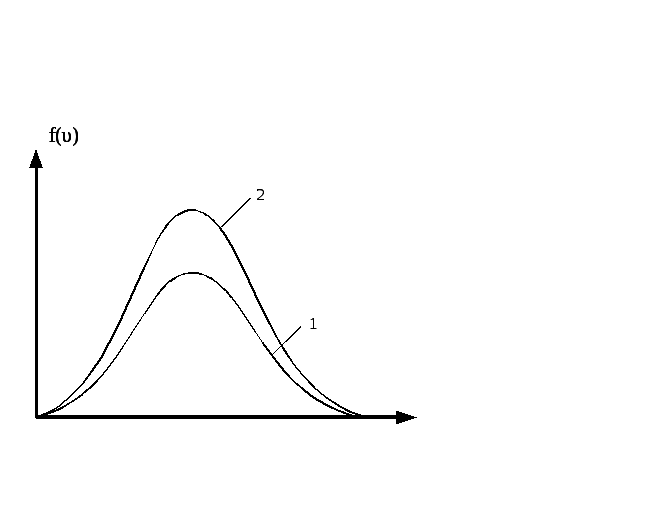
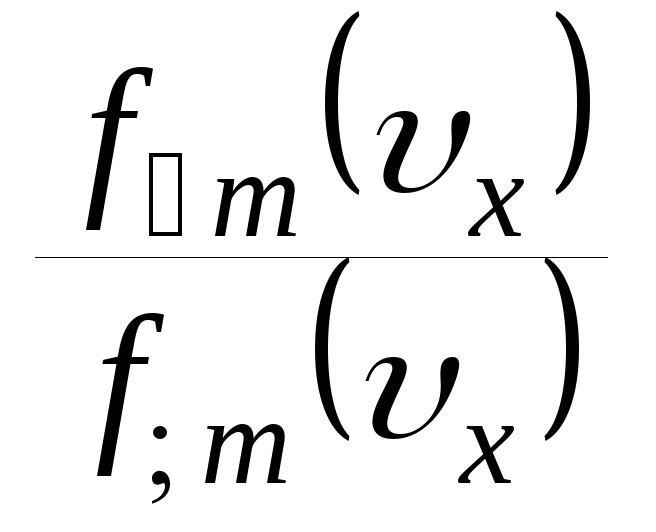 .
Ответ дайте в виде:
.
Ответ дайте в виде: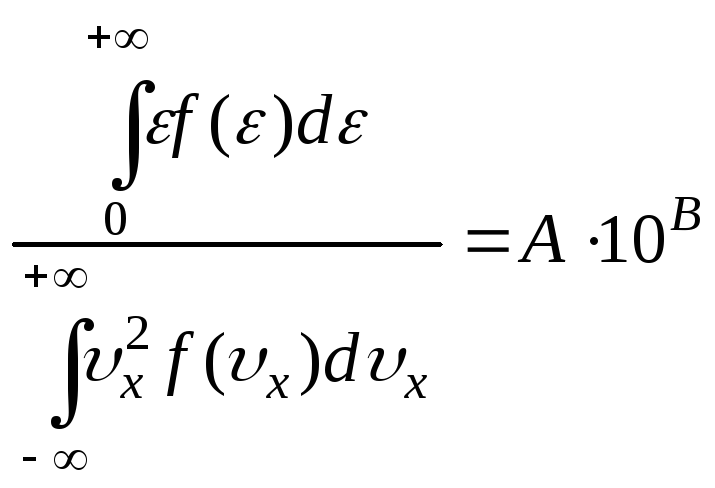 ,
где A
и B
– целые числа, значения которых
перечислите через точку с запятой …
, … без учета размерностей. (*Ответ:
5; -19)
,
где A
и B
– целые числа, значения которых
перечислите через точку с запятой …
, … без учета размерностей. (*Ответ:
5; -19)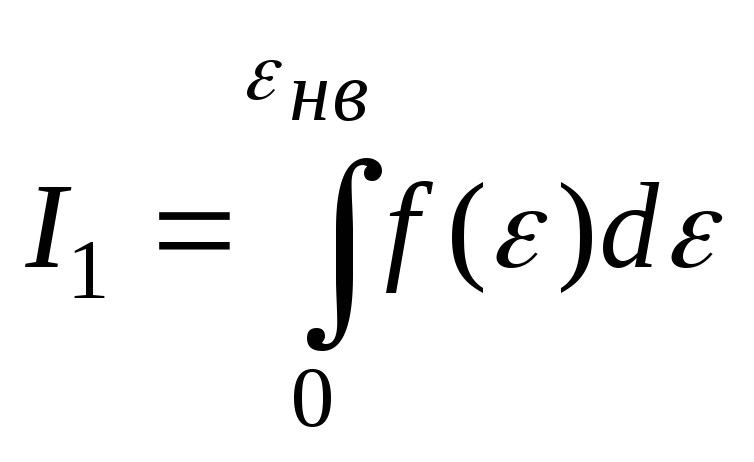 и
и