
Задача 2
Задан импульс
Гаусса
 ,
,
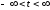 и определено
и определено
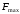 (см. задачу
1). Необходимо:
(см. задачу
1). Необходимо:
а)
определить интервал дискретизации
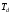 ,
привести таблицу отсчетов
,
привести таблицу отсчетов
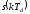 ,
построить график дискретного сигнала
,
построить график дискретного сигнала
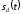 ;
;
б)
определить частоту дискретизации
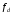 и построить график амплитудного спектра
отсчетов для области частот
и построить график амплитудного спектра
отсчетов для области частот
 .
Показать на графике граничные частоты
полосы пропускания и полосы задержки
фильтра, который восстанавливает сигнал
по отсчетам;
.
Показать на графике граничные частоты
полосы пропускания и полосы задержки
фильтра, который восстанавливает сигнал
по отсчетам;
в) представить
схемы аналого-цифрового преобразователя
(АЦП) и цифро-аналогового преобразователя
(ЦАП); объяснить принцип аналого-цифрового
и цифро-аналогового преобразований;
представить сигнал
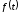 цифровым сигналом, определить длительность
двоичного символа
цифровым сигналом, определить длительность
двоичного символа
 .
.
Решение
а) Расчет интервала дискретизации и отсчетов сигнала
Согласно теореме
Котельникова во время дискретизации
сигнала
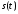 интервал дискретизации
интервал дискретизации
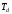 не превышает значения
не превышает значения
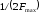 ,
где
,
где
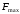 – максимальная частота спектра сигнала
– максимальная частота спектра сигнала
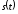 .
Значение
.
Значение
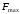 найдено в задаче
1. Рациональным
будет выбрать
найдено в задаче
1. Рациональным
будет выбрать
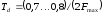 .
.
Отсчеты сигнала
– это значения
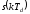 ,
где
,
где
 ;
;
 ,
,
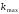 – номера граничных отсчетов, которые
определяются из условий, что при
– номера граничных отсчетов, которые
определяются из условий, что при
 и при
и при
 значения
значения
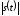 меньше чем половина шага квантования
меньше чем половина шага квантования
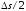 .
Поскольку заданный сигнал – четная
функция, то
.
Поскольку заданный сигнал – четная
функция, то
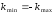
В задаче
1 найдено
значение максимальной частоты спектра
сигнала
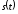 :
:
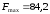 .
Тогда
.
Тогда
 мс. Примем
мс. Примем
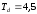 мс. Рассчитаем отсчеты сигнала
мс. Рассчитаем отсчеты сигнала
 ,
аналитическое выражение которого
приведенного в задаче
1 (1).
Рассчитанные отсчеты представлены
таблице 2.1.
,
аналитическое выражение которого
приведенного в задаче
1 (1).
Рассчитанные отсчеты представлены
таблице 2.1.
График
дискретного сигнала
 ,
построенного на основании рассчитанных
отсчетов, приведено на рисунке 2.1.
,
построенного на основании рассчитанных
отсчетов, приведено на рисунке 2.1.

Рисунок 2.1 – График дискретного сигнала
Таблица 2.1 – Отсчеты сигнала, квантования и кодирования уровней квантования
|
|
|
|
|
|
|
|
Кодовые комбинации |
|
-3 |
-13,5 |
0,4 |
0,8 |
1 |
0,5 |
0,1 |
00001 |
|
-2 |
-9,0 |
2,4 |
4,8 |
5 |
2,5 |
0,1 |
00101 |
|
-1 |
-4,5 |
7,0 |
14 |
14 |
7 |
0 |
01110 |
|
0 |
0 |
10 |
20 |
20 |
10 |
0 |
10100 |
|
1 |
4,5 |
7,0 |
14 |
14 |
7 |
0 |
01110 |
|
2 |
9,0 |
2,4 |
4,8 |
5 |
2,5 |
0,1 |
00101 |
|
3 |
13,5 |
0,4 |
0,8 |
1 |
0,5 |
0,1 |
00001 |
б) Построение графика спектра дискретного сигнала
Для построения
графика достаточно помнить, что
спектральная плотность отсчетов – это
сумма периодических повторений с
периодом частоты дискретизации
 спектральной плотности непрерывного
сигнала
спектральной плотности непрерывного
сигнала
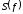 умноженная на
умноженная на
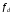 (частота дискретизации
(частота дискретизации
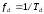 – величина, обратная интервалу
дискретизации):
– величина, обратная интервалу
дискретизации):
![]()
(2.1)
В задании б)
задачи 1
найдена спектральная плотность
непрерывного сигнала, а интервал
дискретизации – в задании а)
задачи
2. частота
дискретизации
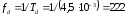 Гц. Для удобства возьмем
Гц. Для удобства возьмем
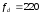 Гц.
Гц.
Построим график
спектральной плотности
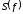 для
положительных частот путем нанесения
точек графика рис. 1.2 – это будет
составляющая ряда с
для
положительных частот путем нанесения
точек графика рис. 1.2 – это будет
составляющая ряда с
 .
Потом строим два смещенных вправо на
.
Потом строим два смещенных вправо на
 и
и
 графика – это будут составляющие ряда
с
графика – это будут составляющие ряда
с
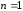 и
и
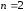 соответственно. Амплитудный спектр
дискретного сигнала рассчитывается
как модуль суммы значений трех графиков.
Расчеты проводятся в области
соответственно. Амплитудный спектр
дискретного сигнала рассчитывается
как модуль суммы значений трех графиков.
Расчеты проводятся в области
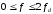 .
Результаты расчетов представлены на
рисунке 2.2.
.
Результаты расчетов представлены на
рисунке 2.2.

Рисунок 2.2 – Спектр дискретного сигнала
На рисунке 2.3
показана АЧХ ФНЧ, который используется
для восстановления непрерывного сигнала
по отсчетам. Его параметры – граничные
частоты полосы пропускания
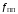 и полосы задержки
и полосы задержки
 .
Эти параметры выбираются из условий:
.
Эти параметры выбираются из условий:
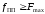 ,
,
 .
.
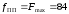 Гц,
Гц,
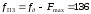 Гц.
Гц.
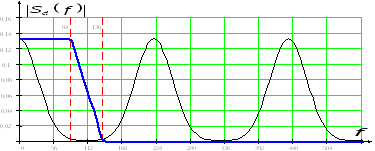
Рисунок 2.3 – Спектр дискретного сигнала и АЧХ восстанавливающего ФНЧ
в) Представление непрерывного сигнала цифровым сигналом
Схема аналого-цифрового преобразователя (АЦП) должна иметь дискритезатор, квантователь и кодер отсчетов, а схема цифроаналогового преобразователя (ЦАП) – декодер и ФНЧ.
Для представления
непрерывного сигнала цифровым сигналом
необходимо выполнить квантование
отсчетов
 и кодирование их двоичным кодом. В
результате равномерного квантования
квантованные отсчеты
и кодирование их двоичным кодом. В
результате равномерного квантования
квантованные отсчеты
 принимают только лишь значения, кратные
шагу квантования
принимают только лишь значения, кратные
шагу квантования
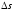 :
:
 ,
где
,
где
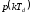 – целое число, уровень квантования.
Квантование – замена отсчета
– целое число, уровень квантования.
Квантование – замена отсчета
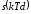 ближайшим квантованным значением
ближайшим квантованным значением
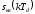 ,
которое однозначно описывается числом
,
которое однозначно описывается числом
 .
При таком приближенном представлении
отсчетов возникает ошибка квантования
.
При таком приближенном представлении
отсчетов возникает ошибка квантования
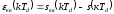 .
Ее значение по модулю не превышает
половины шага:
.
Ее значение по модулю не превышает
половины шага:
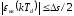 .
Расчет уровней квантования выполняется
по соотношению
.
Расчет уровней квантования выполняется
по соотношению
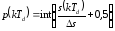
(2.2)
где
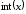 – целое от
– целое от
 .
.
Кодирование уровней
квантования заключается в записи
 в двоичной системе счисления. Код должен
быть равномерным, то есть все кодовые
комбинации должны иметь одинаковое
количество двоичных символов. Длина
кода
в двоичной системе счисления. Код должен
быть равномерным, то есть все кодовые
комбинации должны иметь одинаковое
количество двоичных символов. Длина
кода
 – это целое число, которое выбирается
из условий, что
– это целое число, которое выбирается
из условий, что
 ,
где
,
где
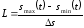 – количество уровней квантования;
– количество уровней квантования;
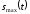 и
и
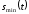 – возможные соответственно максимальное
и минимальное значение сигнала
– возможные соответственно максимальное
и минимальное значение сигнала
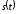 .
.
Длительность
двоичного символа определяется простым
соотношением
 .
.
Выполним квантование
рассчитанных отсчетов, с условием, что
шаг квантования
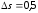 мВ, и кодирование уровней квантования.
Сигнал
мВ, и кодирование уровней квантования.
Сигнал
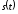 имеет
имеет
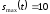 мВ и
мВ и
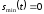 ,
откуда
,
откуда

(2.3)
Из условий, что
 ,
длина кода
,
длина кода
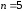 .
.
Результаты расчетов приведены в таблице 2.1.
На рисунке 2.4 представлена соответственная временная диаграмма цифрового сигнала.
Длительность
двоичного символа
 мс.
мс.
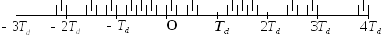 Рисунок
2.4 –
Представление данного сигнала в цифровой
форме
Рисунок
2.4 –
Представление данного сигнала в цифровой
форме

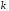
 ,
мс
,
мс ,
мВ
,
мВ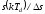

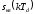 ,
мВ
,
мВ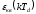 ,
мВ
,
мВ