8.Законы Кирхгофа в операторной форме

I:

II:

Составляя изображения функции времени и представляя в виде двух полиномов.

Рассмотрим разветвленную схему и найдём в ней токи в операторном виде.

Найдём полное сопротивление цепи:

(2)

(3)

Для нахождения тока I₃ запишем выражение для параллельных ветвей точек а и b:

(4)

Подставив сюда найденные значения I₁(p) найдём ток I₃(p)

(5)

Рассмотрим выражение (3) в зависимости от величины приложенной ЭДС:

1)Если приложена постоянная ЭДС, т.е. в этом случае

I₁(p)= степень полинома числителя меньше степени полинома знаменателя.

2) Если к цели приложено переменное напряжение.

e(t) =Em∙sin(ωt+ψ) --> комплексная форма: , следовательно в операторной форме ЭДС будет представлено:

Если обозначить высшую степень оператора р в полиноме N(p) через n, а высшую степень оператора р в полиноме оператора М(р) m, то n<m. Во всех физически реализуемых цепях при воздействии любых встречающихся ЭДС всегда n<m.

Если решить уравнение М(р)=0, найдём соответственно m-корней. Часть из них определяется характером приложенных ЭДС; остальные корни обусловлены свойствами самой цепи её конфигурации.

9.Порядок решения задач операторным методом:

1)Записываются интегро-дифференциальные уравнения Кирхгофа для цепи, где исследуются переходный процесс.

2)Записываются те же уравнения операторной форме для изображений с учётом независимых начальных условий.

3)Эти уравнения решаются алгебраически

4)На основе полученного изображения находится оригинал искомой функции(т.е.)находится функция времени

Последнюю операцию можно осуществить двумя пунктами:1) состоит в применении формул соответствия между функция оператор р и функции времени. В литературе приводятся формулы соответствия охватывающие всё возможные практические задачи.

2) состоит в применении формулы разложения этот способ рассматривают как основной для перехода от изображения к функции времени.

Формула разложения

Переход от изображения к функции времени сложно осуществить с помощью формулы вида:

Число слагаемых равно числу корней М(рк)=0.

Примечание: В том случае, если при расчете ПП операторным методом, корни p₁ и p₂ комплексно сопряжённые формула разложения применяемая в заданном случае имеет вид:

Комплексная форма

10. Сравнение различных методов расчёта пп.

Классические и операторные методы можно применять для решения задач любой сложности решение уравнений 1 и 2-го порядка для постоянной и синусоидальной ЭДС целесообразно проводить классическим методом, а 3-го и более высоких порядков операторным методом.

Если воздействующее напряжение интеграла Дюамеля, когда воздейств. напряжения изменяются по сложному закону.

Если характеристическое уравнение имеет высокую степень(5-7 степень) целесообразно применять спектральный методом отсчёта ПП.

11.Электрические цепи с не синусоидальными периодическими токами.

На практике токи и ЭДС существенно отличаются от постоянной или синусоидальной формы в цепях содержащих не линейные сопротивления ёмкости или индуктивности даже при воздействии синусоидальной ЭДС возникнут не синусоидальные напряжения и токи.

Примеры таких токов и напряжений:

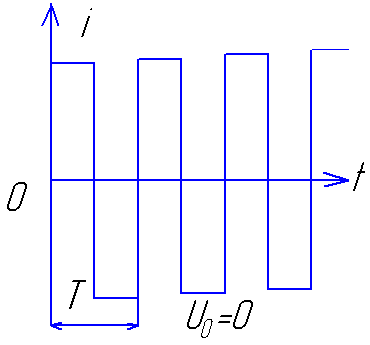
I₀ – постоянная составляющая I₀0